
- •15. Аналитическая геометрия
- •15.1. Плоскость в пространстве
- •I уровень
- •II уровень
- •III уровень
- •15.2. Уравнения прямой в пространстве. Взаимное
- •I уровень
- •II уровень
- •III уровень
- •15.3. Прямая и плоскость в пространстве
- •I уровень
- •II уровень
- •III уровень
- •15.4. Поверхности второго порядка
- •I уровень
- •II уровень
- •III уровень
15. Аналитическая геометрия
в пространстве
15.1. Плоскость в пространстве
Пусть P
– плоскость, для которой требуется
построить уравнение,![]() – произвольная точка этой плоскости.
– произвольная точка этой плоскости.
1. Если задана точка
![]() плоскостиРи два неколлинеарных
вектора
плоскостиРи два неколлинеарных
вектора![]() и
и![]() параллельных данной плоскости, то
справедливовекторно-параметрическое
уравнение плоскостиP
параллельных данной плоскости, то
справедливовекторно-параметрическое
уравнение плоскостиP
![]() (15.1)
(15.1)
где
![]() – радиус-вектор точки
– радиус-вектор точки![]()
![]()
Запись уравнения (15.1) в координатной форме
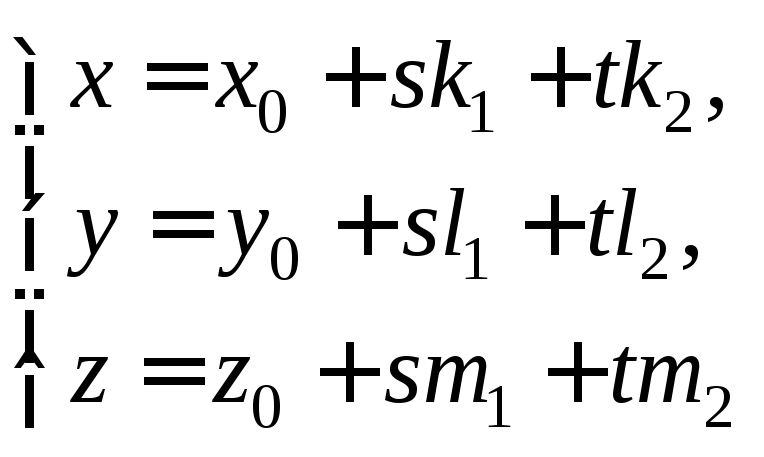 (15.2)
(15.2)
называется параметрическими уравнениями плоскости.
Кроме того, исходные данные позволяют записать уравнение плоскости Ри с помощью определителя
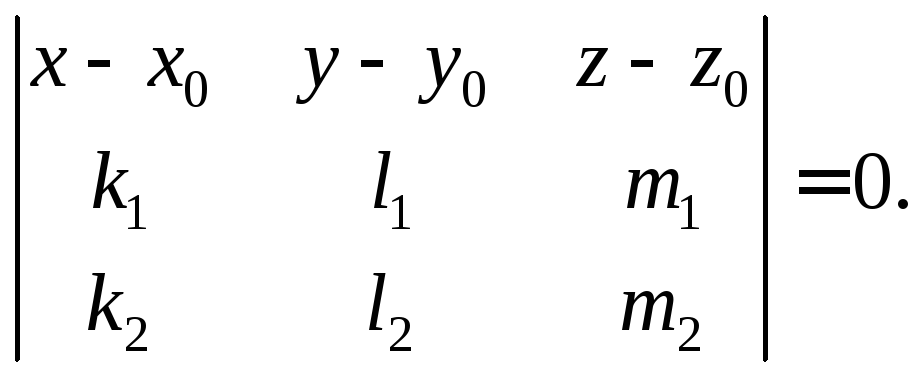 (15.3)
(15.3)
2. Если известны
три точки
![]()
![]()
![]() плоскостиP, не лежащие
на одной прямой, то аналогично (15.3) можно
построить уравнение плоскости, проходящей
через три заданные точки,
плоскостиP, не лежащие
на одной прямой, то аналогично (15.3) можно
построить уравнение плоскости, проходящей
через три заданные точки,
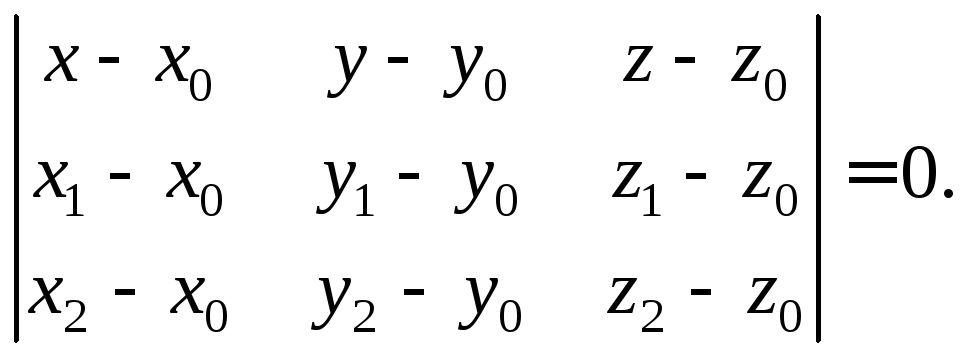 (15.4)
(15.4)
3. Если известны точки пересечения плоскости Pс координатными осями, т. е.M0(a, 0, 0),M1(0, b, 0),M2(0, 0, c), то справедливо уравнение плоскости «в отрезках»
![]() (15.5)
(15.5)
4. Если задан
нормальный вектор
![]() и точка
и точка![]() плоскостиР, то справедливо уравнение
плоскостиР, то справедливо уравнение
![]() (15.6)
(15.6)
на основании которого выводится общее уравнение плоскости P
![]()
где
![]()
5. В качестве
нормального вектора плоскости Pможно взять единичный вектор![]() направленный из начала координат в
сторону плоскости, т. е.
направленный из начала координат в
сторону плоскости, т. е.![]() где
где![]()
![]()
![]() Тогда справедливо нормальное уравнение
плоскости
Тогда справедливо нормальное уравнение
плоскости
![]() (15.7)
(15.7)
где
![]() – расстояние от начала координат до
плоскости.
– расстояние от начала координат до
плоскости.
Величина
![]() (15.8)
(15.8)
называется
отклонением точкиМ0от плоскостиР. При этом:![]() еслиМ0иO(0,
0, 0) лежат по одну сторону от плоскости;
еслиМ0иO(0,
0, 0) лежат по одну сторону от плоскости;![]() – если лежат по разные стороны;
– если лежат по разные стороны;![]() если
если![]() Расстояние
Расстояние![]() от точкиМ0до плоскостиРравно абсолютному значению ее отклонения,
т. е.
от точкиМ0до плоскостиРравно абсолютному значению ее отклонения,
т. е.
![]()
От общего уравнения плоскости к нормальному можно перейти с помощью умножения на нормирующий множитель
![]() (15.9)
(15.9)
Расстояние
![]() от точки
от точки![]() до плоскостиР, заданной общим
уравнением
до плоскостиР, заданной общим
уравнением![]() может быть найдено по формуле
может быть найдено по формуле
![]() (15.10)
(15.10)
Угол между плоскостями в пространстве
определяется по косинусу угла между
нормальными векторами![]() и
и![]() этих плоскостей:
этих плоскостей:
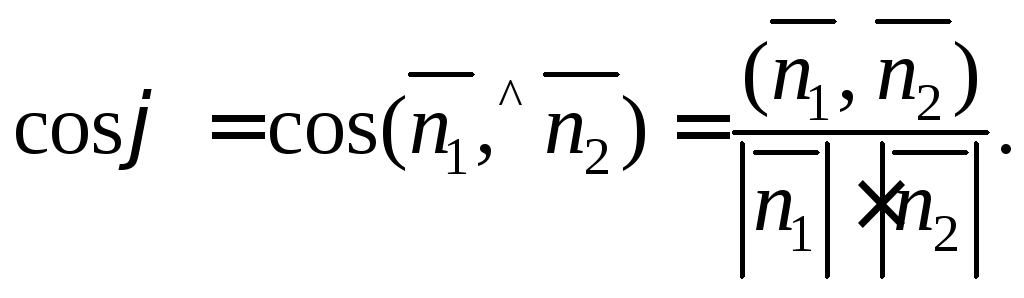 (15.11)
(15.11)
Пример
1.
Записать общее уравнение плоскости,
проходящей через точку
![]() параллельно векторам
параллельно векторам![]() и
и![]()
Решение.
1-й способ.
Поскольку векторы
![]() и
и![]() не коллинеарны (их соответствующие
координаты не являются пропорциональными),
то, согласно формуле (15.3), справедливо
уравнение
не коллинеарны (их соответствующие
координаты не являются пропорциональными),
то, согласно формуле (15.3), справедливо
уравнение
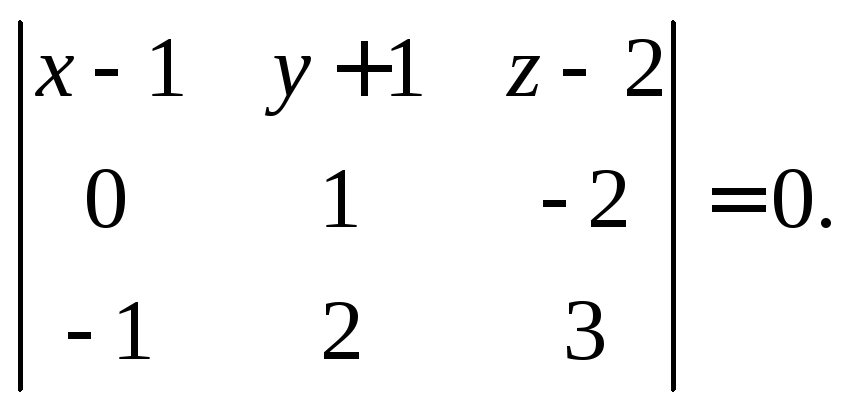
Преобразуем левую часть:
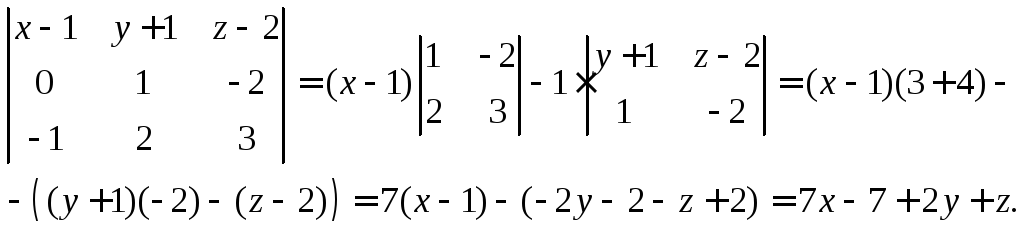
Таким образом, получаем общее уравнение искомой плоскости:
![]()
2-й
способ.
Найдем нормальный вектор плоскости,
используя векторное произведение
векторов
![]() и
и![]()
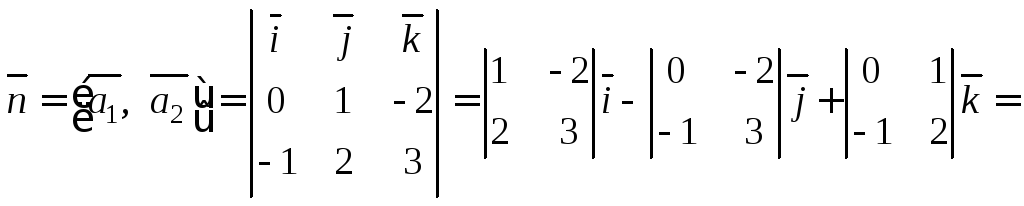
![]()
Тогда, согласно уравнению (15.6), имеем:
![]()
![]()
Пример
2.
Записать общее уравнение плоскости P,
проходящей через точки
![]() и
и![]() параллельно вектору
параллельно вектору![]()
Решение.
Векторы
![]() и
и![]() не коллинеарны. Если точка
не коллинеарны. Если точка![]() –
произвольная точка плоскости, то векторы
–
произвольная точка плоскости, то векторы![]()
![]() и
и![]() компланарны. Поэтому, согласно формуле
(15.3), уравнение плоскости имеет вид:
компланарны. Поэтому, согласно формуле
(15.3), уравнение плоскости имеет вид:
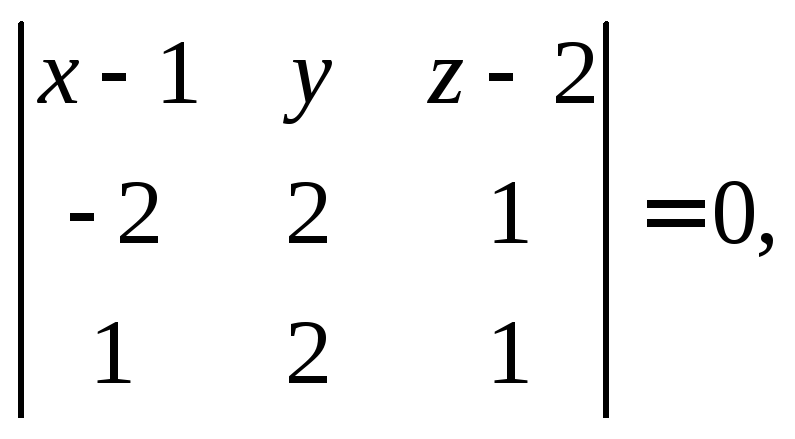
откуда
получаем общее уравнение
![]()
Задачу можно решить и вторым способом, если найти нормальный вектор плоскости (см. 2-й способ решения примера 1).
Пример
3.
Записать уравнение плоскости
![]()
1) «в отрезках»;
2) в параметрическом виде.
Решение.
Запишем уравнение плоскости в виде
![]() откуда после деления на –2 получим
искомое уравнение «в отрезках»:
откуда после деления на –2 получим
искомое уравнение «в отрезках»:
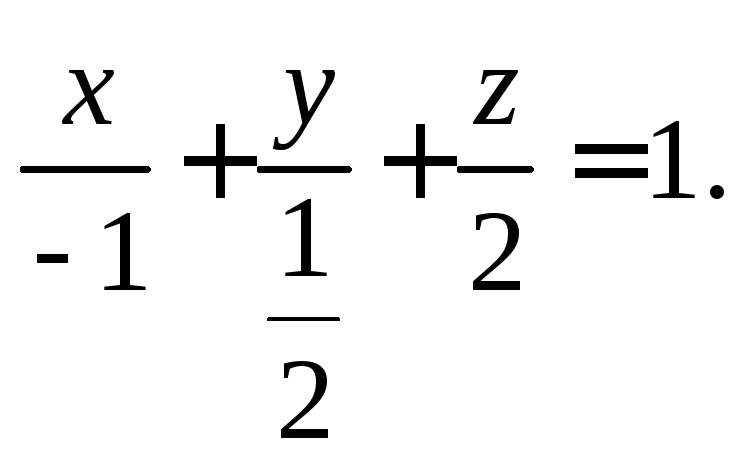
Из
полученного уравнения «в отрезках»
имеем точки
![]()
![]() и
и![]() которые лежат в заданной плоскости.
Тогда в качестве двух неколлинеарных
векторов
которые лежат в заданной плоскости.
Тогда в качестве двух неколлинеарных
векторов![]() и
и![]() параллельных плоскости, можно взять
параллельных плоскости, можно взять![]() и
и![]() Используя параметрические уравнения
плоскости (15.2), получим:
Используя параметрические уравнения
плоскости (15.2), получим:
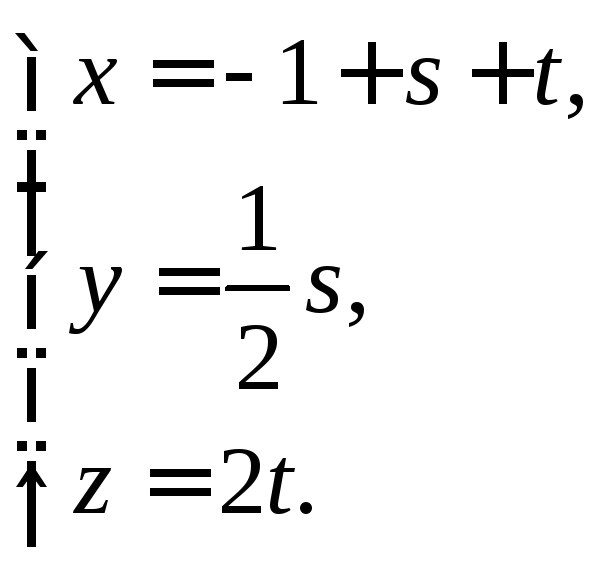
Это и есть параметрические уравнения заданной плоскости.
Пример
4. Привести
к нормальному виду уравнение плоскости
![]() найти единичный нормальный вектор
плоскости и расстояние до нее от начала
координат.
найти единичный нормальный вектор
плоскости и расстояние до нее от начала
координат.
Решение. Запишем нормальное уравнение плоскости. Так как 21 – это свободный член уравнения плоскости, то по формуле (15.9) вычисляем нормирующий множитель
![]()
Тогда нормальным уравнением будет:
![]()
Значит,
![]() а расстояние от начала координат до
плоскости равно 3.
а расстояние от начала координат до
плоскости равно 3.
Пример
5. Найти
уравнения плоскостей, делящих пополам
двугранные углы, образованные плоскостями
![]() и
и![]()
З а м е ч а н и е. Такие плоскости называются биссекторными.
Решение.
Пусть точка
![]() принадлежит искомой плоскости. Тогда
принадлежит искомой плоскости. Тогда![]() т. е. выполняется равенство
т. е. выполняется равенство
![]()
которое приводит к двум уравнениям
![]() или
или
![]()
Таким образом, задача имеет два решения:
![]()
Заметим,
что это две взаимно перпендикулярные
плоскости. Действительно,
![]()
![]() и
и![]() т. е.
т. е.![]() а значит,
а значит,![]()
Пример
6.
Определить, пересекает ли плоскость
![]() отрезокAB,
если A(1,
–1, 2) и B(2,
4, –3).
отрезокAB,
если A(1,
–1, 2) и B(2,
4, –3).
Решение.
Данная плоскость P
пересекает отрезок AB
тогда и
только тогда, когда
![]() По формуле (15.8) находим:
По формуле (15.8) находим:
![]()
![]()
Значит,
![]() Следовательно, плоскость пересекает
отрезок.
Следовательно, плоскость пересекает
отрезок.
Пример
7. Составить
уравнения плоскостей, параллельных
плоскости
![]() и отстоящих от нее на расстояние
и отстоящих от нее на расстояние![]()
Решение.
Пусть
![]() – точка искомой плоскости. Тогда,
используя формулу расстояния (15.10),
имеем:
– точка искомой плоскости. Тогда,
используя формулу расстояния (15.10),
имеем:
![]()
т. е.
![]()
Отсюда получаем уравнения искомых плоскостей
![]() и
и
![]()
Пример
8.
Составить уравнение плоскости, проходящей
через точки A(1,
0, –1), B(1,
3, –4) и образующей угол
![]() с плоскостью
с плоскостью![]()
Решение. Не ограничивая общности, будем искать уравнение плоскости в виде
![]()
Поскольку точки A(1, 0, –1) и B(1, 3, –4) лежат в искомой плоскости, то их координаты удовлетворяют уравнению этой плоскости. Значит, имеем:
![]()
откуда
![]()
![]() Подставим найденные значенияD
и B,
выраженные через C,
в уравнение плоскости:
Подставим найденные значенияD
и B,
выраженные через C,
в уравнение плоскости:
![]()
Следовательно,
нормальный вектор есть
![]()
Воспользуемся
тем, что плоскость образует угол
![]() с плоскостью
с плоскостью![]() нормальный вектор которой
нормальный вектор которой![]() .
По формуле косинуса угла между плоскостями
(15.11) имеем:
.
По формуле косинуса угла между плоскостями
(15.11) имеем:
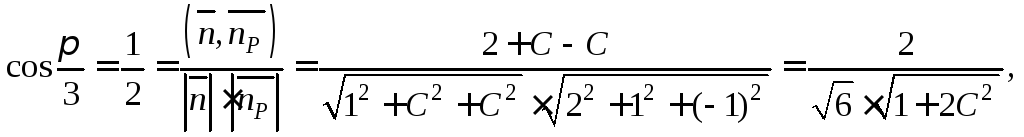
откуда
![]() или
или![]() НаходимC,
преобразовывая последнее равенство:
НаходимC,
преобразовывая последнее равенство:
![]()
![]()
![]()
![]()
Окончательно имеем уравнения двух плоскостей:
![]() и
и
![]()
Задания
