18. Функции многих переменных

18.1. Основные понятия теории функций

многих переменных

Пусть задано множество точек координатной плоскости Если каждой упорядоченной паре действительных чиселставится в соответствие единственное действительное числоz, то говорят, что на множествеDзаданафункция двух переменныхсо значениями вRи пишут:

или

где

Множество Dназываетсяобластью определенияфункцииf. Множествосостоящее из всех чиселz, равныхгденазываетсямножеством значенийфункции.

Множество называется открытым, если каждая точка множества принадлежит ему вместе с некоторой окрестностью этой точки. Множество называетсясвязным, если любые две точки этого множества можно соединить непрерывной кривой, целиком принадлежащей этому множеству.

Множество, обладающее свойствами открытости и связности, называется областью.

Точка Mназываетсяграничнойточкой областиD, если в любой ее окрестности содержатся точки как принадлежащиеD, так и не принадлежащиеD.

Совокупность всех граничных точек области называется границейэтой области.

Замкнутой областьюназывается объединение области и ее границы.

Область называется ограниченной, если все ее точки содержатся в некотором круге конечного радиуса с центром в начале системы координат.

Область называетсяодносвязной, если для любой замкнутой кривой, принадлежащей этой области, ограниченная ею часть плоскости целиком принадлежит областиD. В противном случае – областьмногосвязная. Многосвязная область называетсяn-связной, если ее граница состоит изnзамкнутых кривых.

Графиком функцииопределенной на областиD, называется множество точекпространстваR³, гдеи

Множество точек для которых(т. е. функция имеет постоянное значениеС), называетсялинией уровня функции

С помощью линий уровня изучают вид графика функции двух переменных.

Пусть D– множество точек пространстваR³. Если каждой точкепоставлено в соответствие единственное числото говорят, что на множествеDзаданафункция трех переменныхи пишут:

или

где

Графиком функции определенной областиDназывается множество точекпространстваR⁴, где

Поверхностью уровняфункции трех переменныхназывается множество точектаких, что

Понятие функции нескольких переменных обобщается на любое

С помощью поверхностей уровня изучают вид графика функции трех переменных.

Пусть G– множество точек пространстваRⁿ,Если каждой точкепоставлено в соответствие единственное числото говорят, что на множествеGопределенафункция n переменныхи пишут:

График функции переменных находится в пространствеЕго невозможно изобразить геометрически для

Для функции нескольких переменных можно определить понятие предела и непрерывности. Приведем эти понятия для функции двух переменных.

Пусть некоторая точка областиМножество точекдля которых выполняется неравенство

называется -окрестностью точки М₀.

Число А называется пределом функции в точке М₀ (при ), еслитакое, что для любой точкиудовлетворяющей условиювыполняется неравенство

Обозначают:

или

Функция называетсянепрерывной в точке если

или

Функция fназываетсянепрерывной в области D, если она непрерывна в каждой точке этой области.

Аналогичным образом определяются понятия предела и непрерывности в точке для функции nпеременных,

Пример 1. Найти область определения функции

Решение. Заданная функция определена, если т. е.Областью определения функции является часть плоскости, лежащая вне эллипса(рис. 18.1).

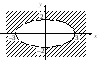
Рис. 18.1

Пример 2. Найти область определения функции

Решение. Функция u определена при условии т. е.Областью определения является часть плоскости, заключенная между двумя прямымиивместе с точками этих прямых (рис. 18.2).

Рис. 18.2

Пример 3. Найти область определения функции

Решение. Данная функция трех переменных определена при условии т. е.

Областью определения функции u является часть пространства, находящаяся вне однополостного гиперболоида (рис. 18.3).

Рис. 18.3

Пример 4. Найти линии уровня функции

Решение. Уравнение семейства линий уровня имеет вид:

или

Рассмотрим те значения C, которые приводят к различным ответам.

Если то линии уровня не существует. ЕслиC = –1, то линия уровня вырождается в точку (–1; 0). Если C > –1, то в качестве линий уровня получим концентрические окружности с центром в точке (–1; 0).

Пример 5. Найти поверхности уровня функции

Решение. Уравнение семейства поверхностей уровня имеет вид: ЕслиC = 0, то получаем: илиЭтим уравнением задается конус. ЕслиC > 0, то – семейство однополостных гиперболоидов. Если C < 0, то – семейство двуполостных гиперболоидов.

Пример 6. Вычислить предел функции:

1) 2) 3)

Решение. 1) Так как ито числитель дроби стремится к 1, а знаменатель стремится к нулю, т. е. является бесконечно малой величиной. Следовательно, заданная дробь – бесконечно большая величина и

2) Преобразуем выражение

Теперь, используя первый замечательный предел и свойства пределов при иполучим:

3) Представим функцию в виде 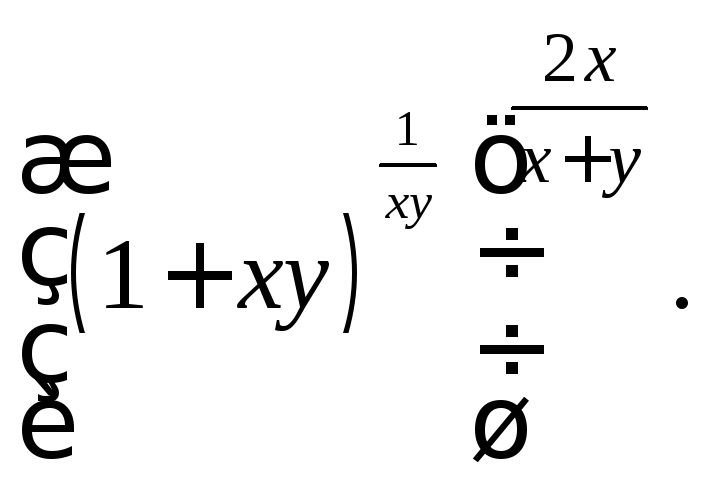Так как прииимеемто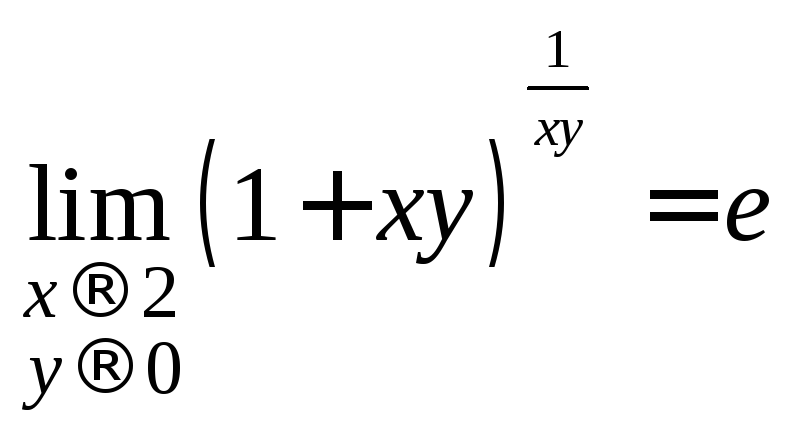(второй замечательный предел). Показательпристремится к 2. Поэтому получаем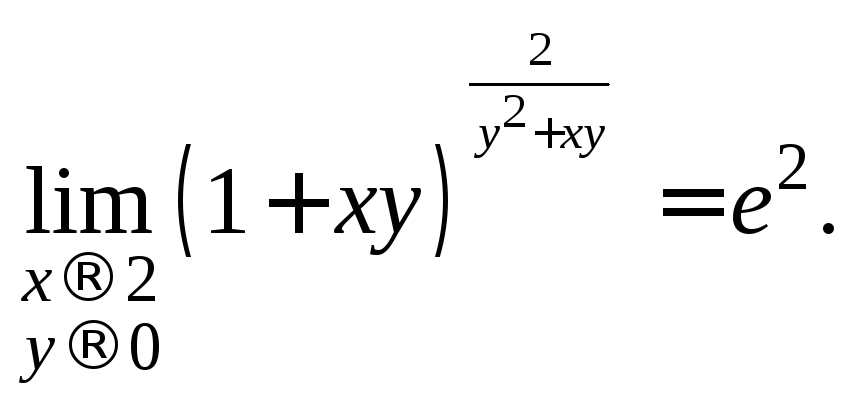

Пример 7. Найти точки разрыва функции

Решение. Данная функция не определена в тех точках, где знаменатель дроби обращается в нуль: т. е. функция не определена для точек прямыхиВ остальных точках плоскости функция определена. В любой точкеM на прямых илифункция не является непрерывной, так какне существует. Таким образом, любая точка прямыхиесть точка разрыва заданной функции. В любой точкеM₁, не лежащей на прямых илизаданная функция непрерывна.

Задания