I уровень
1.1. Найдите частные производные первого порядка функции:
1)
2)
3)
4)
1.2. Найдите полный дифференциал функции:
1)
2)
3)
4)
1.3.Вычислите приближенно значение:
1)
2)
3)
II уровень
2.1.Найдите частные производные и вычислите их значения в указанной точкеМ0:
1)
2)
3)
4)
5)
6)
2.2.Найдите дифференциал функции в точкеМ0:
1)
2)
3)
4)
2.3.Вычислите приближенно:
1)
2)
3)
4)
2.4.Вычислите:
1)
если
2)
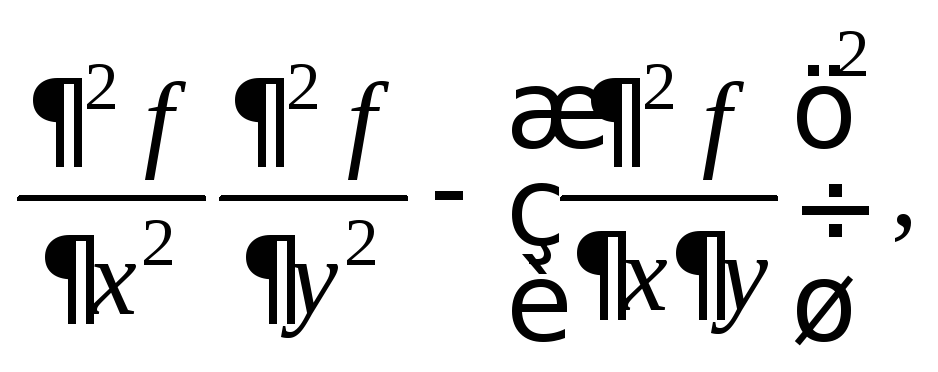если
3)
если
III уровень
3.1.Определите,
существует ли частная производная
функции
в точке (1; 0).
3.2.Установите,
имеет ли заданная функция частные
производные в точке
и дифференцируема ли она в этой точке:
1)
2)
3)
4)
5)
6)
3.3. Найдите частные производные функции:
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
3.4.Покажите,
что функция
удовлетворяет уравнению
3.5.Вычислите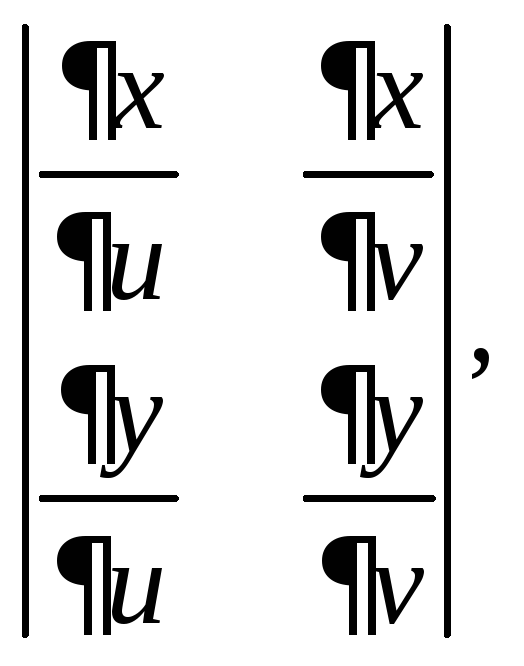
если
3.6. Найдите
если
18.3. Дифференцирование сложных функций
Пусть
где
причем
имеет непрерывные частные производные,
функции
имеют непрерывные производные,t– независимая переменная. Тогдапроизводная сложной функции
вычисляется по формуле
(18.9)
Пусть
и
гдеx– независимая
переменная, причем функция
имеет непрерывные частные производные,
– непрерывную производную. Тогда
справедливаформула полной производнойфункцииzпоx:
(18.10)
Пусть
и
причем функция
имеет непрерывные частые производные
поxиy,
а функции
имеют непрерывные частные производные
поuиv.
Тогда частные производные функцииzпоuиvнаходят по формулам:
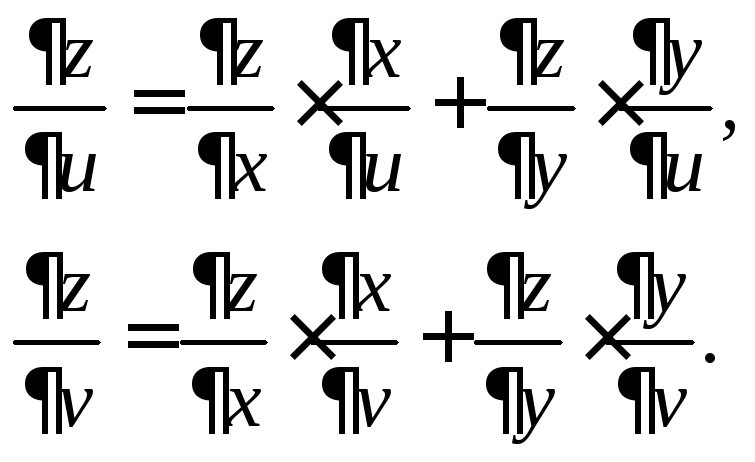(18.11)
Формулы (18.9)–(18.11) обобщаются на любое конечное количество переменных (зависимых и независимых).
Пример
1. Найти
двумя способами (свести к функции одной
переменнойt
и по формуле (18.9)), если
где
Решение.
1-й способ.
Подставив вместо x,
y
заданные выражения, получим:
– функцию одной переменнойt.
Тогда
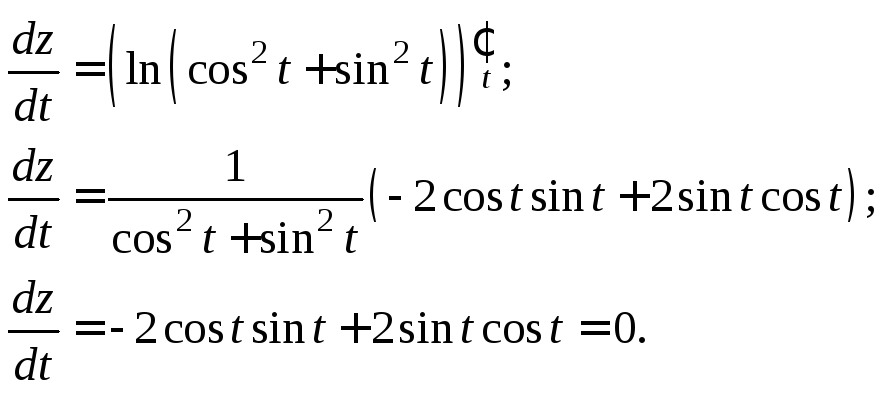
2-й способ. Найдем частные производные по x и y функции z:
Вычисляем
производные функций
и
По формуле (18.9) получаем:
Заменив x и y их выражениями через t, получим:
Пример
2. Вычислить
в точке
если
где
Решение.
Находим
частные производные заданной функции
Вычисляем
По формуле (18.9) получаем:
Делаем замену переменных:
Вычислим
значение
в точке
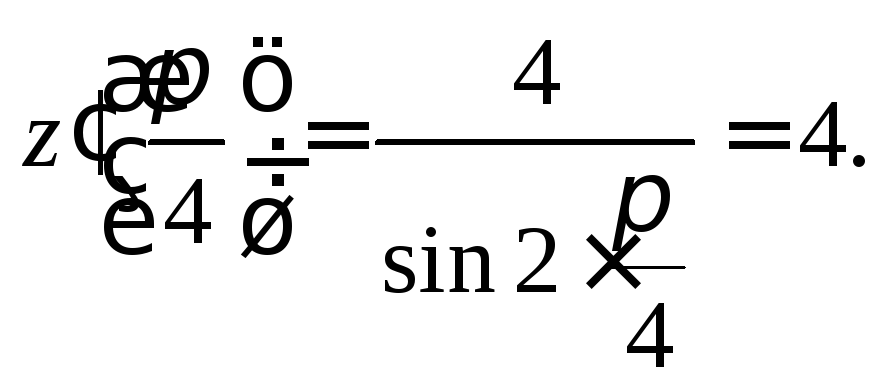
Пример
3. Вычислить
различными способами
функции
где
Решение. 1-й способ. Используем метод логарифмического дифференцирования. Прологарифмируем равенство, задающее функцию:
или
Дифференцируем
по
полученное равенство, считая
Подставляя вместо z и y заданные выражения из условия, получаем:
2-й способ. Найдем частные производные:
Вычисляем производную функции у:
Теперь по формуле (18.10) получаем:
или
Пример
4. Найти
функции
если
Решение. Используя формулу (18.11), найдем частные производные:
По формуле (18.11) получим:
или
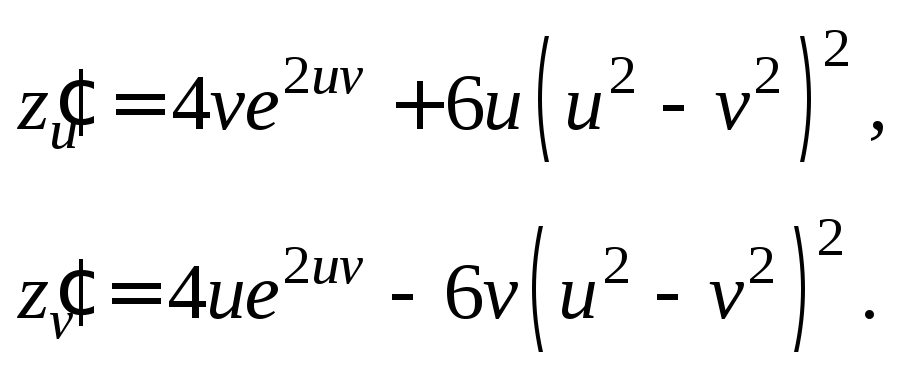
Заметим, что этот пример можно решать и вторым способом – вначале подставить вместо x, y их выражения через u, v, а затем – найти частные производные по u, v.
Пример
5. Найти
функции
где
при
Решение.
1-й способ.
Подставив в исходную функцию
получим
функцию одной переменной:
Дифференцируем по x:
2-й способ. Найдем частные производные:
а также производные:
По формуле (18.10) получаем:
После замены переменных получим:
Пришли
к такому же аналитическому выражению
для
что и в первом способе решения.
Вычислим
в точке
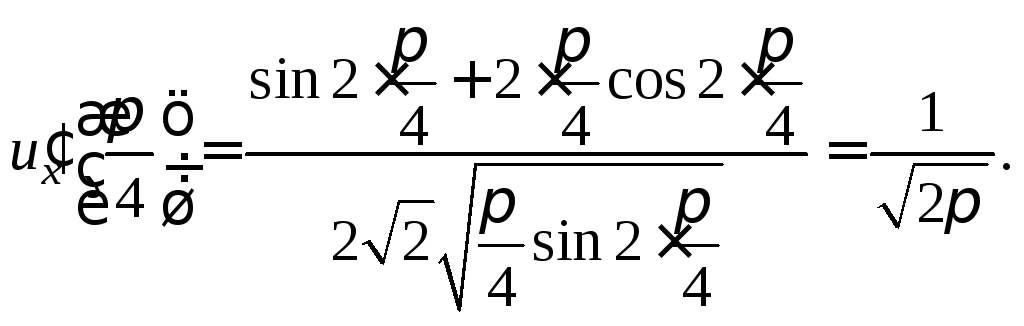
Задания