16. Предел и непрерывность функции

16.1. Предел функции в точке и на бесконечности

Определение предела функции по Гейне было дано в § 10.3.

Определение по Коши. Число А называется пределом функции f(x) в точке х₀, если функция определена в некоторой выколотой окрестности точки х₀ и если для любого сколь угодно малого числа существует такое числочто для всехх, удовлетворяющих условию

(16.1)

выполняется

(16.2)

Это записывают так:

Число А называется пределом функции на бесконечности (при или), если для любогосуществует числочто для всехх, удовлетворяющих условию

выполняется неравенство

Это записывают так:

или

Определение предела функции в точке (на бесконечности) по Гейне и Коши эквивалентны.

Функция f(x) называется бесконечно большой при если для всякого числаМ > 0 существует число что для всехх, удовлетворяющих условию

(),

выполняется неравенство

Это записывают так:

Если f(x) – бесконечно большая функция при то она не имеет предела в этой точке (на бесконечности). Символ предела в данном случае используют лишь для обозначения.

Функция f(x) называется бесконечно малой при если

Свойства предела функции в точке

1. Если функция f(x) имеет предел в точке х₀, то существует окрестность этой точки (за исключением, быть может, самой точки х₀), на которой функция ограничена.

2. Если существует предел функции f(x) в точке х₀, равный числу то существует такая окрестность точких₀, на которой функция имеет тот же знак, что и число А.

3. Если функции f(x) и g(x) имеют пределы в точке х₀, то:

где

(16.3)

(16.4)

(16.5)

где

Формулы (16.3) и (16.4) обобщаются на любое конечное количество слагаемых и множителей. В случае их бесконечного количества равенство выполняется не всегда.

Аналогичные свойства верны и для предела функции на бесконечности.

Если в результате непосредственного использования формул (16.3) – (16.5) возникают неопределенности типа то вначале необходимо тождественно преобразовать выражение, стоящее под знаком предела (то же для неопределенностей).

Свойства бесконечно малых и бесконечно больших

функций

1. Число А является пределом функции f(x) в точке х₀ тогда и только тогда, когда существует бесконечно малая функция притакая, что

2. Сумма и произведение конечного числа бесконечно малых (бесконечно больших) функций при является бесконечно малой (бесконечно большой) функцией.

3. Произведение бесконечно малой функции при на ограниченную функцию является бесконечно малой.

4. Частное при делении постоянной С, на бесконечно малую функцию приявляется бесконечно большой при

5. Частное при делении постоянной С на бесконечно большую функцию при является бесконечно малой при

При вычислении пределов функций удобно применять метод замены переменной, т. е. , где, если.

Пример 1. Пользуясь определением предела функции в точке по Коши, доказать, что

Решение. Зафиксируем произвольное значение

Согласно определению, требуется по  найти такое число чтобы из условияследовало неравенство (16.2), которое в данном случае имеет вид:

(16.6)

Упрощая последнее неравенство, получим:

Откуда, поскольку , имеем:

Получаем:

Следовательно, если принять то из неравенствабудет следовать неравенство (16.6). Это и означает, что

Пример 2. Вычислить пределы:

1) 2)3)

Решение. 1) При подстановке в выражение, стоящее под знаком предела, значения получаем

2) При подстановке в выражение, стоящее под знаком предела, значения получаем неопределенность вида, для раскрытия которой разложим числитель и знаменатель дроби на множители:

Подставив полученные выражения, получим:

3) Непосредственная подстановка значения приводит к неопределенностиЧтобы раскрыть ее, в числителе используем формулу бинома Ньютона, а многочлен в знаменателе разложим по схеме Горнера:

Пример 3. Вычислить

Решение. Представим функцию как произведение двух функцийи

Функция является суммой двух бесконечно малых функций притак какиЗначит– бесконечно малая функция при

Функция является ограниченной, так как значения этой функции будут лежать в промежутке

Получаем произведение бесконечно малой функции на ограниченную

Значит функция f(x) – есть бесконечно малая при т. е.

Пример 4. Вычислить предел функции:

1) 2)

Решение. 1) Непосредственная подстановка в выражение, стоящее под знаком предела, значения дает неопределенностьПреобразуем выражение, стоящее под знаком предела, следующим образом:

Возвращаясь к пределу, получим:

2) При непосредственном вычислении предела получим неопределенность вида . Чтобы избавиться от нее, домножим и разделим выражение на

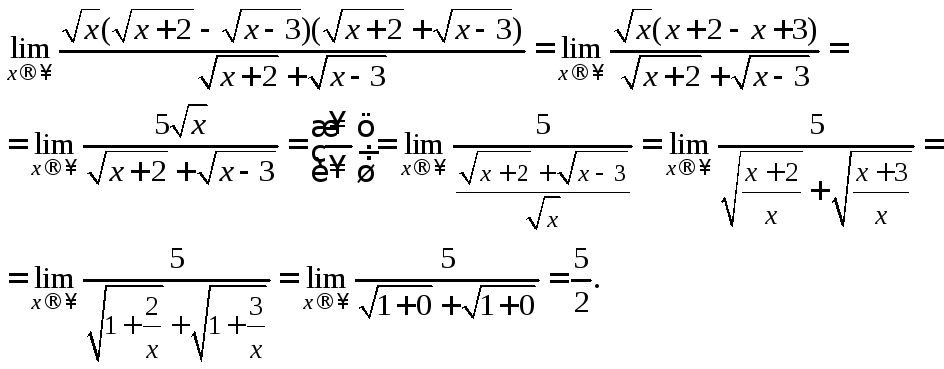
Задания