
- •16. Предел и непрерывность функции
- •16.1. Предел функции в точке и на бесконечности
- •I уровень
- •II уровень
- •III уровень
- •16.2. Замечательные пределы
- •I уровень
- •I уровень
- •II уровень
- •III уровень
- •16.4. Односторонние пределы. Асимптоты
- •I уровень
- •II уровень
- •III уровень
- •16.5. Непрерывность функции. Классификация
- •I уровень
- •II уровень
- •III уровень
I уровень
1.1. Вычислите предел функции:
1)
![]() 2)
2)![]()
3)
![]() 4)
4)![]()
5)
![]() 6)
6)
![]()
7)
![]() 8)
8)
9)
![]() 10)
10)![]()
11)
![]() 12)
12)![]()
1.2. Вычислите предел функции:
1)
![]() 2)
2)![]()
3)
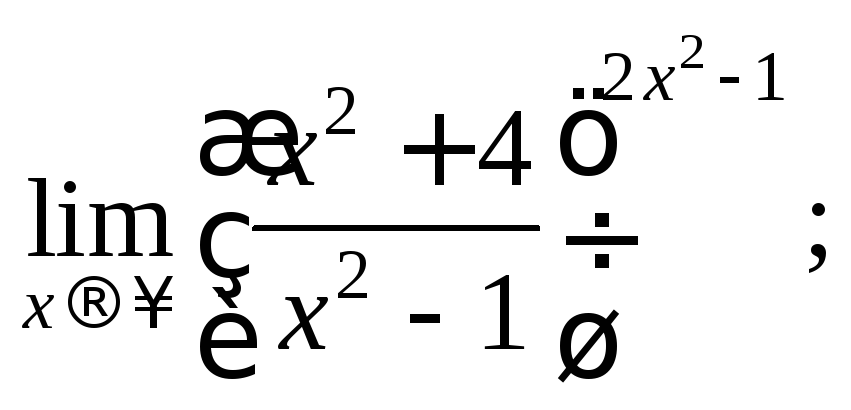 4)
4)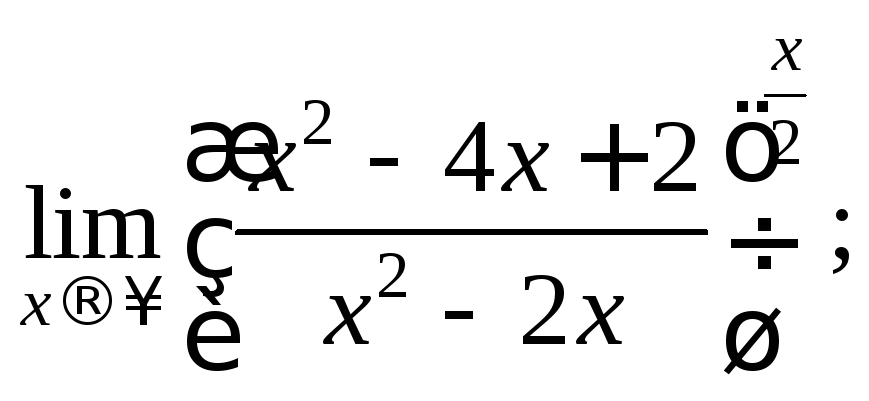
5)
![]() 6)
6)![]()
7)
![]() 8)
8)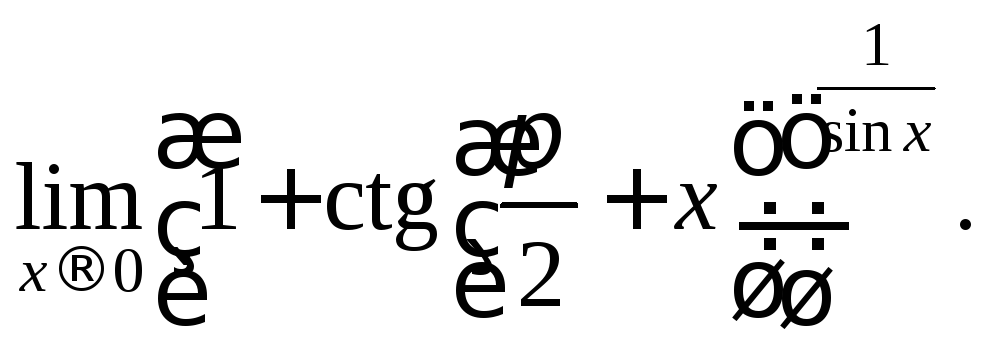
II уровень
2.1. Вычислите предел функции, используя замечательные пределы:
1)
![]() 2)
2)
3)
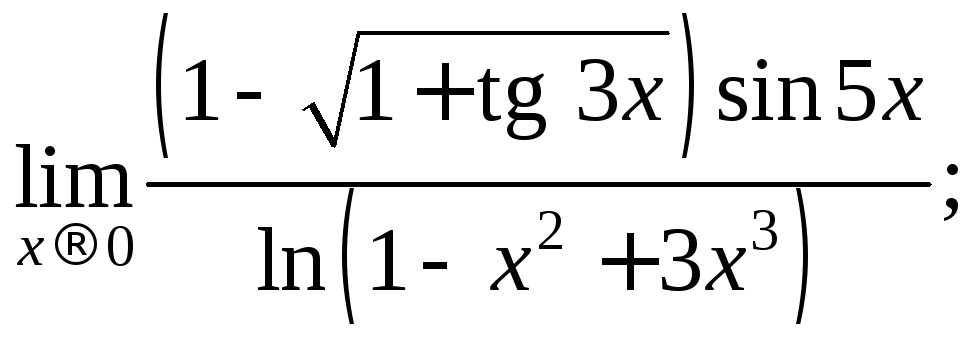 4)
4)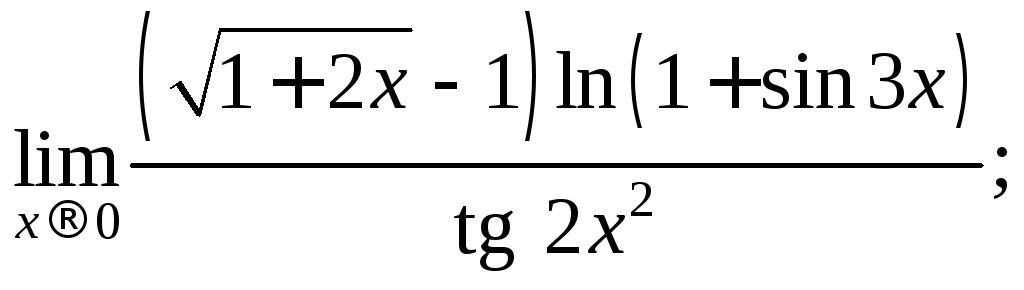
5)
![]() 6)
6)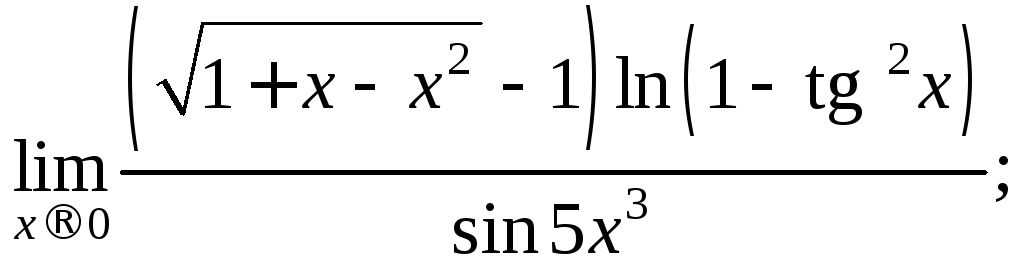
7)
![]()
8)
![]()
2.2. Вычислите пределы функций, сделав соответствующую замену переменной:
1)
![]() 2)
2)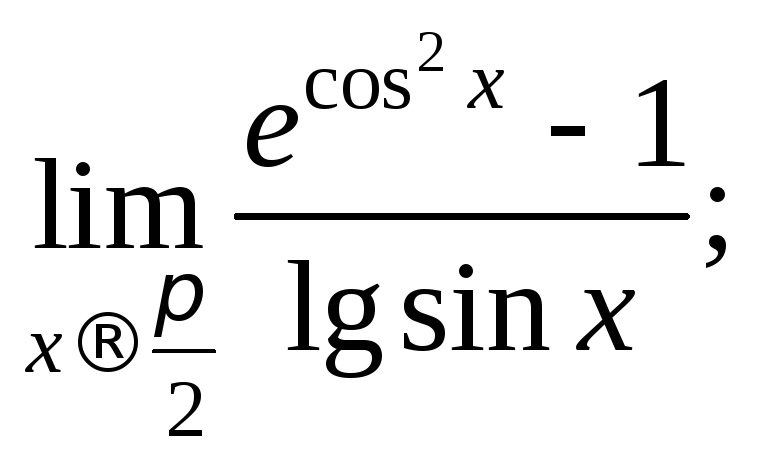
3)
![]() 4)
4)![]()
5)
![]() 6)
6)![]()
7)
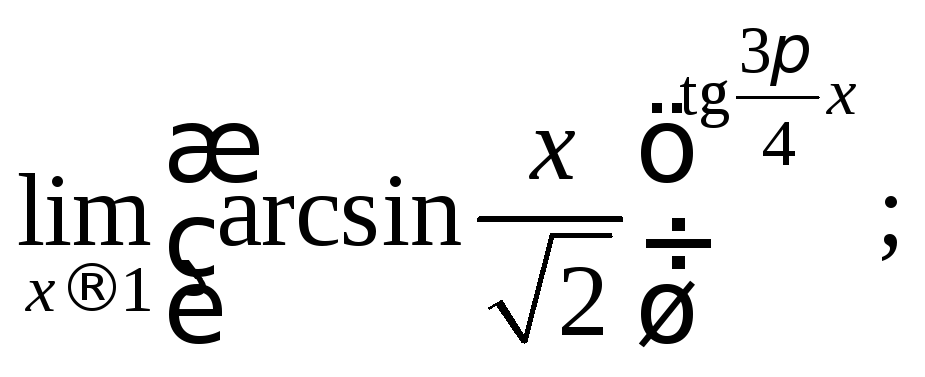 8)
8)
![]()
9)
![]() 10)
10)![]()
11)
![]() 12)
12)
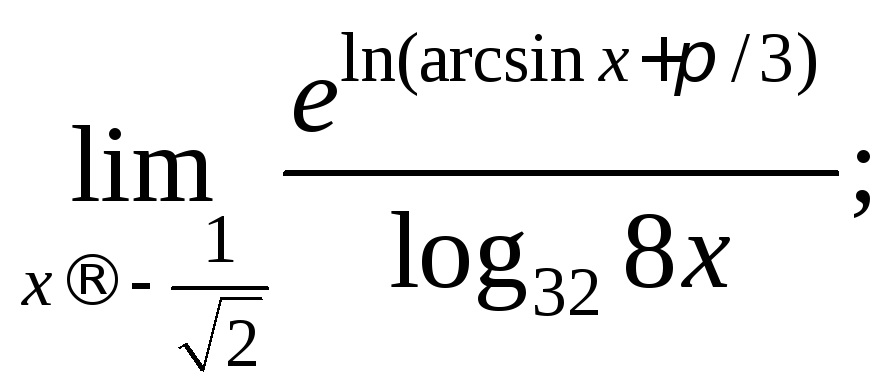
13)
![]() 14)
14)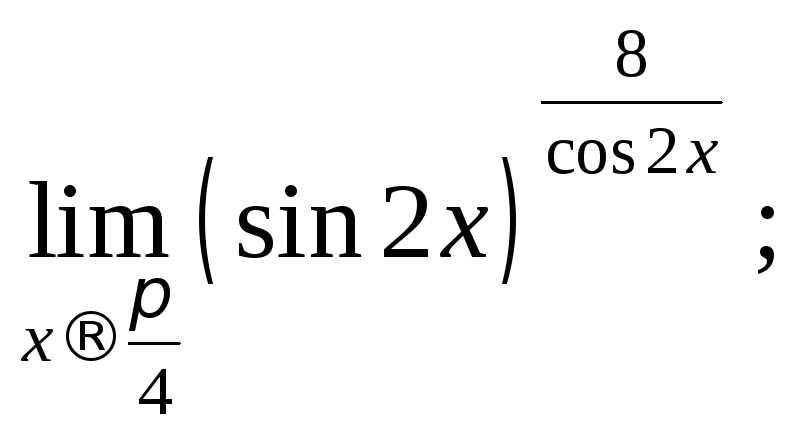
15)
![]() 16)
16)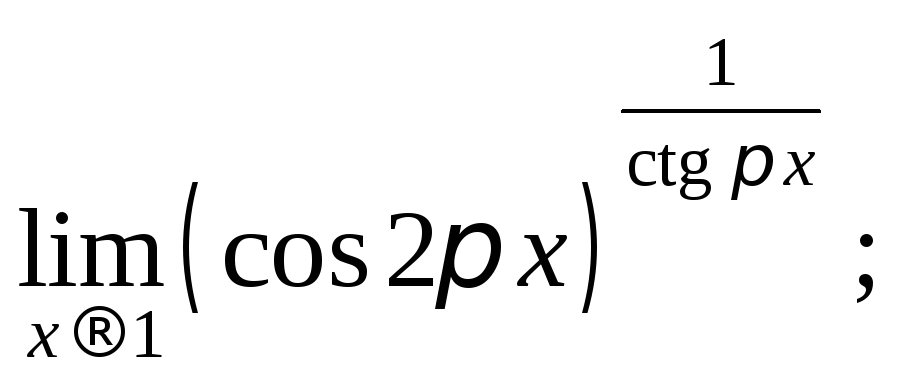
17)
![]() 18)
18)
![]()
19)
![]() 20)
20)![]()
21)
![]() 22)
22)![]()
23)
![]() 24)
24)![]()
III уровень
3.1. Вычислите предел функции:
1)
![]() 2)
2)![]()
3)
![]() 4)
4)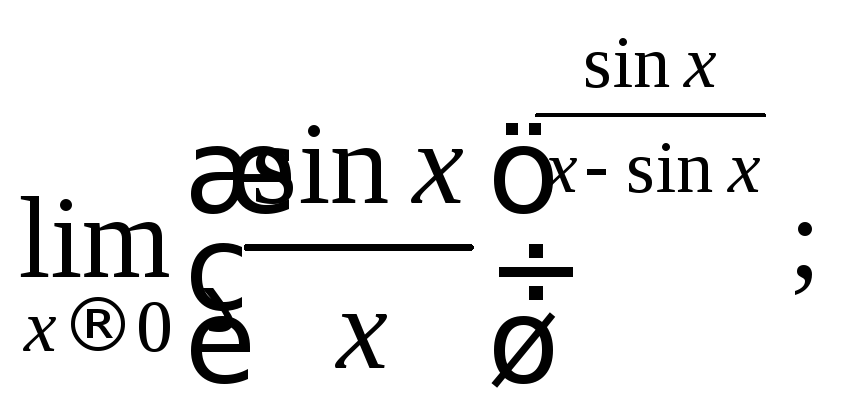
5)
![]() 6)
6)![]()
3.2. Вычислите предел функции, предварительно преобразовав выражение:
1)
![]()
2)
![]()
3)
![]()
16.3. Эквивалентность бесконечно малых функций
Две функции
![]() и
и![]() называются эквивалентными бесконечно
малыми, при
называются эквивалентными бесконечно
малыми, при![]()
![]() ,
если
,
если
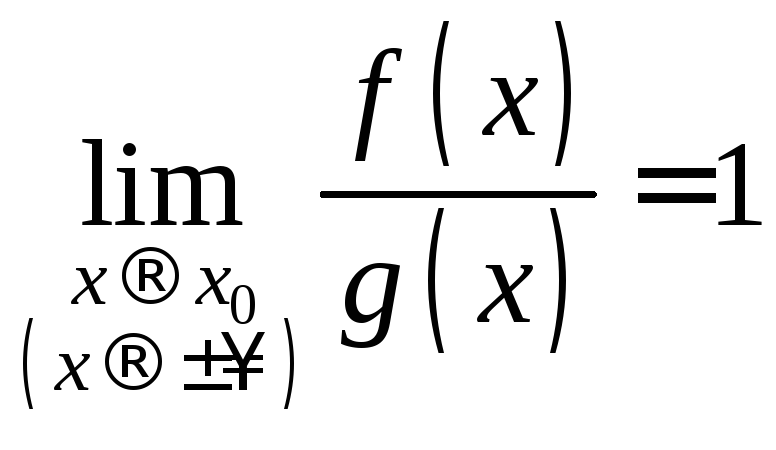 ,
,
это записывают
так:
![]() при
при![]()
![]() .
.
При вычислении пределов функций в точке и на бесконечности удобно пользоваться следующей теоремой:
Теорема.
Если h(x),
f(x)
и g(x)
– некоторые функции, определенные в
окрестности точки
![]() (на числовой полуоси) и
(на числовой полуоси) и![]() при
при![]()
![]() ,
то
,
то
![]() (16.16)
(16.16)
Формула (16.16) показывает, что в произведении можно заменять функцию-сомножитель на эквивалентную ей – более простую для вычисления предела.
Таблица эквивалентных бесконечно малых
Пусть
![]() ,
если
,
если![]()
![]() .
Тогда справедливы следующие эквивалентности:
.
Тогда справедливы следующие эквивалентности:
![]() (16.17)
(16.17)
![]() (16.18)
(16.18)
![]() (16.19)
(16.19)
![]() (16.20)
(16.20)
![]() (16.21)
(16.21)
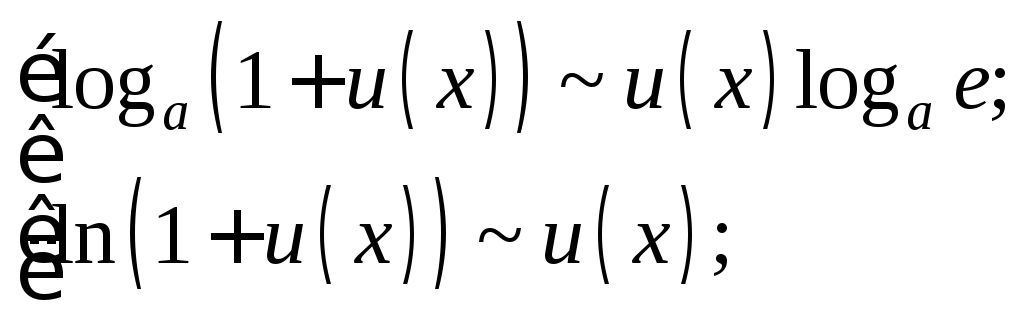 (16.22)
(16.22)
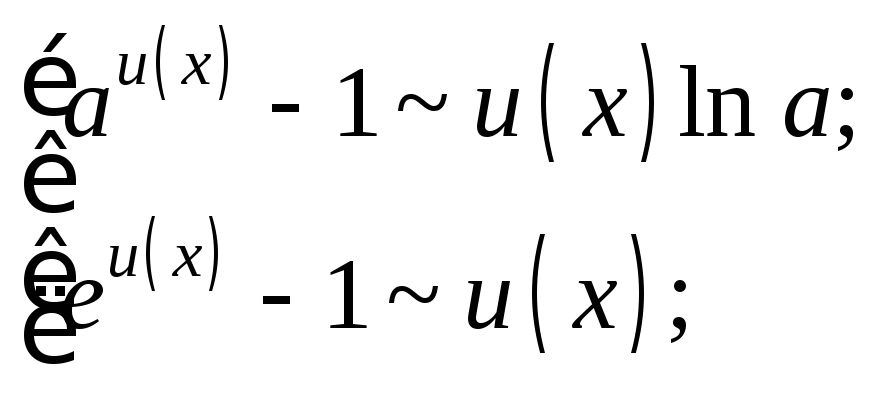 (16.23)
(16.23)
![]() (16.24)
(16.24)
Пример 1. Вычислить предел функции в точке, заменяя бесконечно малые эквивалентными им:
1)
![]() 2)
2)
3)
![]() 4)
4)![]()
Решение.
1) Непосредственное
вычисление предела приводит к
неопределенности вида
![]() .
Используем формулу (16.16), а также формулы
(16.22), (16.24), (16.17) таблицы эквивалентных
функций.
.
Используем формулу (16.16), а также формулы
(16.22), (16.24), (16.17) таблицы эквивалентных
функций.
При этом выполняются
условия
![]()
![]() если
если![]() которые являются обязательными для
перехода к эквивалентным функциям.
Тогда
которые являются обязательными для
перехода к эквивалентным функциям.
Тогда
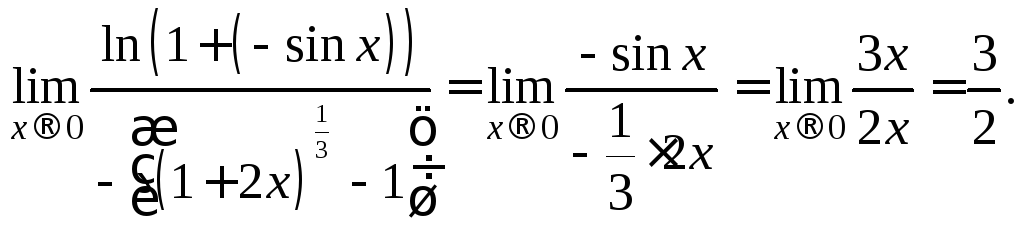
Заметим, что решение примера с таким условием уже дано выше (см. 3-е условие примера 2 из параграфа 16.2).
2) При
подстановке
![]() в выражения получаем неопределенность
вида
в выражения получаем неопределенность
вида![]() .
Чтобы от нее избавиться, воспользуемся
формулами (16.18), (16.23), (16.24) таблицы
эквивалентных бесконечно малых. Поскольку
.
Чтобы от нее избавиться, воспользуемся
формулами (16.18), (16.23), (16.24) таблицы
эквивалентных бесконечно малых. Поскольку![]() то справедливы эквивалентности:
то справедливы эквивалентности:
![]()
![]()
![]()
Подставив полученные эквивалентные функции вместо соответствующих бесконечно малых, получим:

3) Преобразуем выражение, стоящее под знаком предела, и используем формулу (16.19):
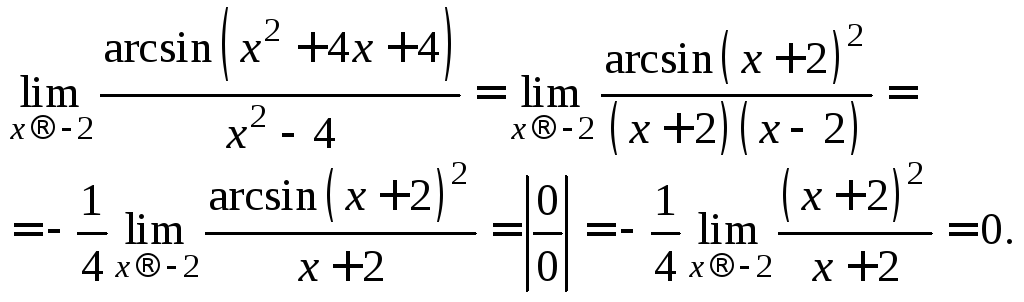
Использование
формулы (16.19) было обосновано тем, что
![]() если
если![]()
4) Замечаем, что
непосредственное вычисление предела
приводит к неопределенности вида
![]() Вместе с тем,
Вместе с тем,![]() если
если![]() а поэтому можем использовать формулу
(16.20). Тогда
а поэтому можем использовать формулу
(16.20). Тогда
![]()
Пример 2.
Вычислить предел:
![]() несколькими способами.
несколькими способами.
Решение.
1-й способ.
При
![]() получим:
получим:
![]() и
и
![]()
Следовательно,
имеем неопределенность вида
![]() .
Сделаем замену переменной. Введем такоеt,
чтобы
.
Сделаем замену переменной. Введем такоеt,
чтобы
![]() если
если
![]()

Далее заменим бесконечно малые в числителе и знаменателе на эквивалентные по формулам (16.21), (16.23), (16.22), (16.18).
Мы имеем право
сделать это, так как для соответствующей
функции u(t)
выполняется
![]() если
если![]() Получаем:
Получаем:
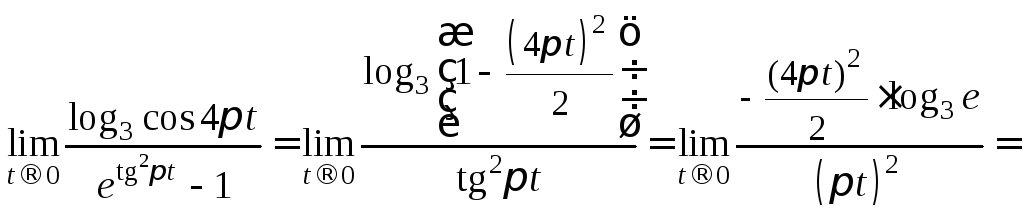
![]()
2-й способ.
Поскольку
при непосредственном вычислении предела
имеем неопределенность вида
![]() то необходимо преобразовать выражение,
стоящее под знаком предела. Однако сразу
использовать таблицу эквивалентности
бесконечно малых нельзя, поскольку
то необходимо преобразовать выражение,
стоящее под знаком предела. Однако сразу
использовать таблицу эквивалентности
бесконечно малых нельзя, поскольку![]() и
и![]() не стремятся к нулю, если
не стремятся к нулю, если![]() Используя свойство периодичности
тригонометрических функций, получаем:
Используя свойство периодичности
тригонометрических функций, получаем:
![]()
Выражение под
знаком предела преобразовано таким
образом, что
![]() и
и![]() если
если![]() Поэтому можно использовать формулы
эквивалентности (16.21), (16.23), (16.22), (16.18). В
результате получаем:
Поэтому можно использовать формулы
эквивалентности (16.21), (16.23), (16.22), (16.18). В
результате получаем:
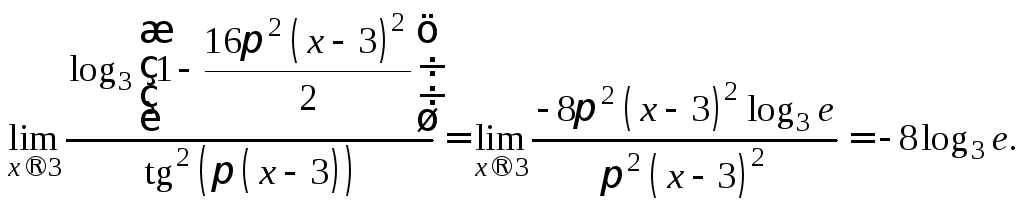
Пример 3. Вычислить предел функции, заменяя бесконечно малые эквивалентными,
![]()
Решение.
Непосредственное вычисление предела
приводит к неопределенности вида
![]() Используем формулы (16.19) и (16.22) таблицы
эквивалентных функций.
Используем формулы (16.19) и (16.22) таблицы
эквивалентных функций.
При этом выполняется
условие
![]() если
если![]() которое является обязательным для
перехода к эквивалентным функциям.
Тогда
которое является обязательным для
перехода к эквивалентным функциям.
Тогда
![]()
Используя далее вторую формулу из (16.12), получаем:
![]()
Задания
