
- •16. Предел и непрерывность функции
- •16.1. Предел функции в точке и на бесконечности
- •I уровень
- •II уровень
- •III уровень
- •16.2. Замечательные пределы
- •I уровень
- •I уровень
- •II уровень
- •III уровень
- •16.4. Односторонние пределы. Асимптоты
- •I уровень
- •II уровень
- •III уровень
- •16.5. Непрерывность функции. Классификация
- •I уровень
- •II уровень
- •III уровень
I уровень
1.1.
Докажите, что функции
![]() и
и![]() являются
эквивалентными бесконечно малыми при
являются
эквивалентными бесконечно малыми при![]()
1)
![]() 2)
2)![]()
3)
![]() 4)
4)![]()
1.2. Вычислите предел функции, заменяя бесконечно малые эквивалентными:
1)
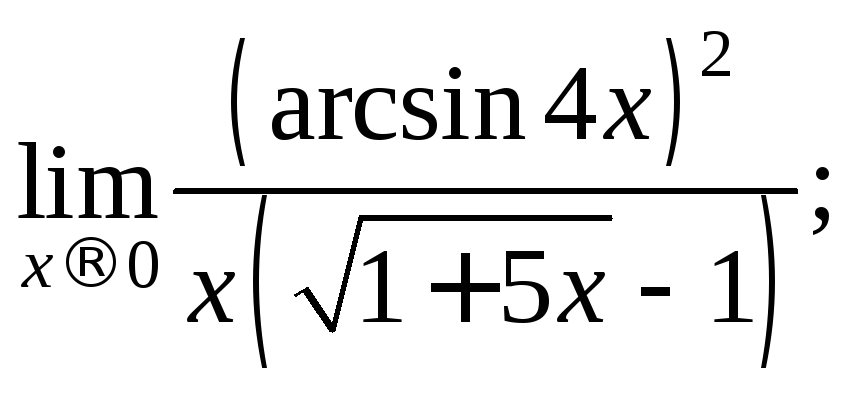 2)
2)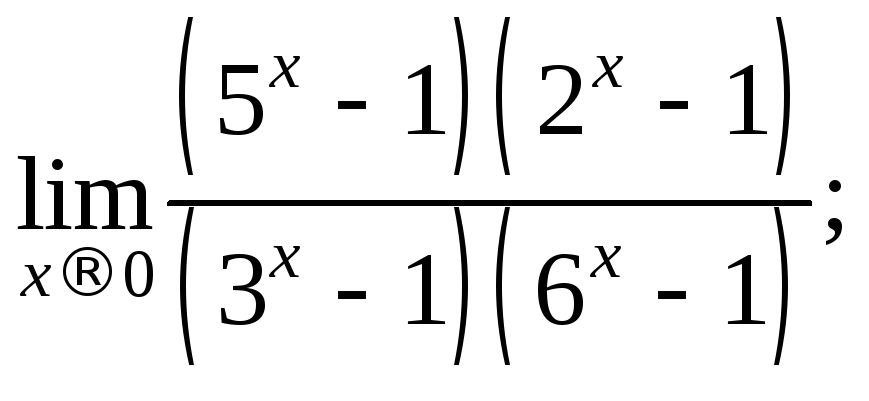
3)
![]() 4)
4)![]() ;
;
5)
![]() 6)
6)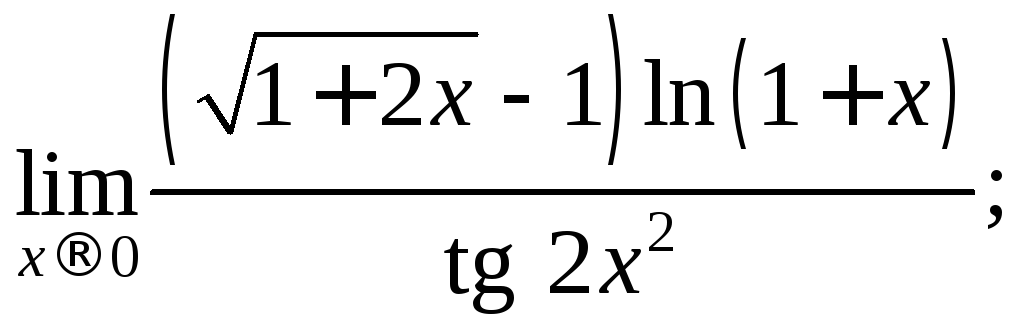
7)
![]() 8)
8)![]()
9)
![]() 10)
10)![]()
11)
![]() 12)
12)![]()
II уровень
2.1. Вычислите предел функции, используя эквивалентность бесконечно малых:
1)
![]()
 2)
2)
3)
 4)
4)![]()
5)
 6)
6)
7)
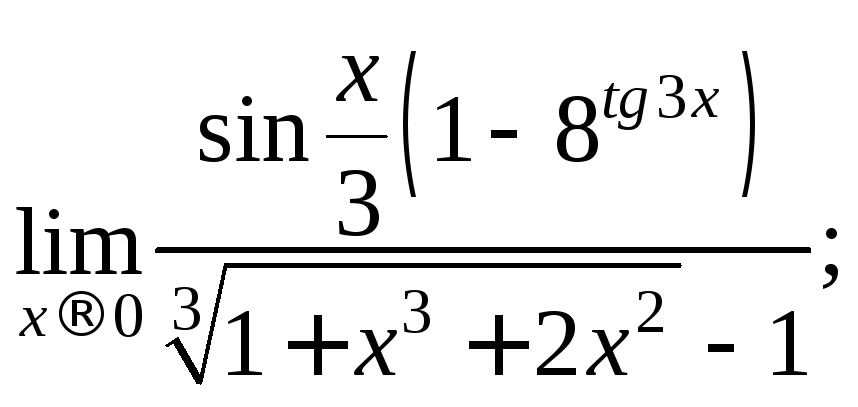 8)
8)
9)
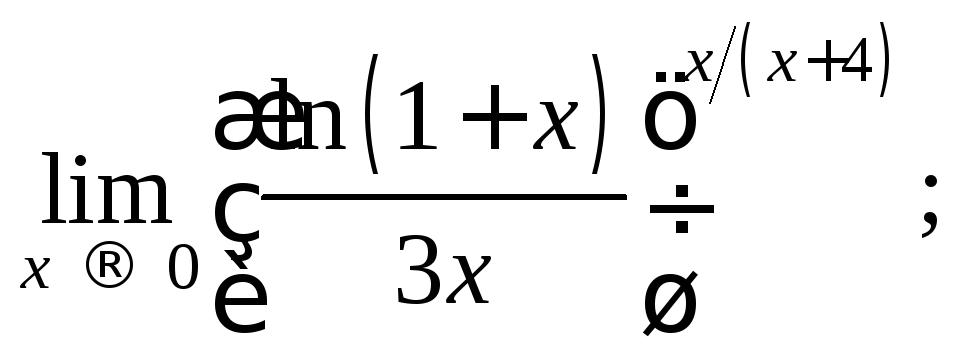 10)
10)

11)
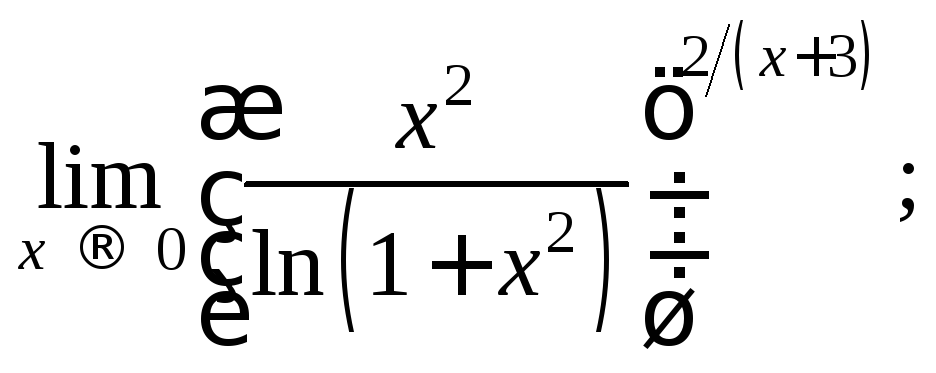 12)
12)
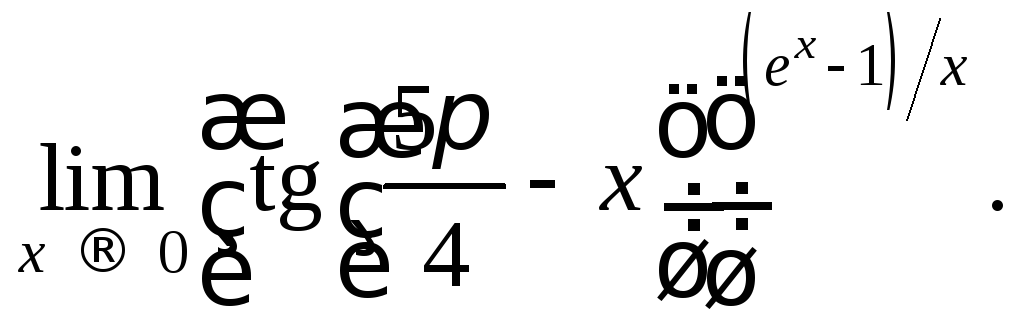
2.2. Вычислите предел функции:
1)
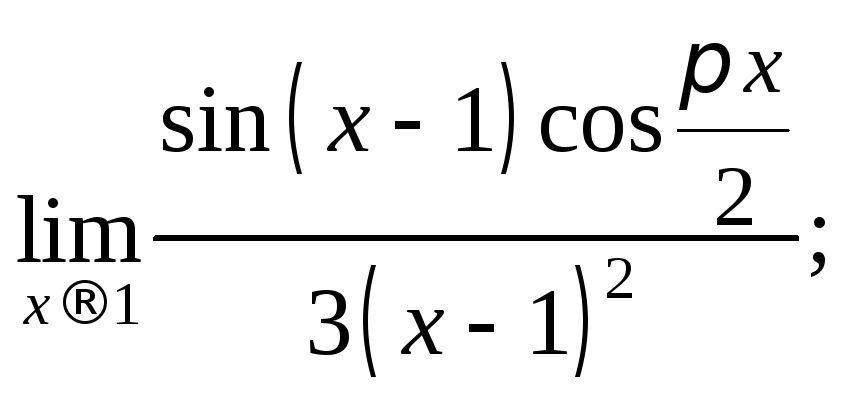 2)
2)![]()
3)
 4)
4)![]()
5)
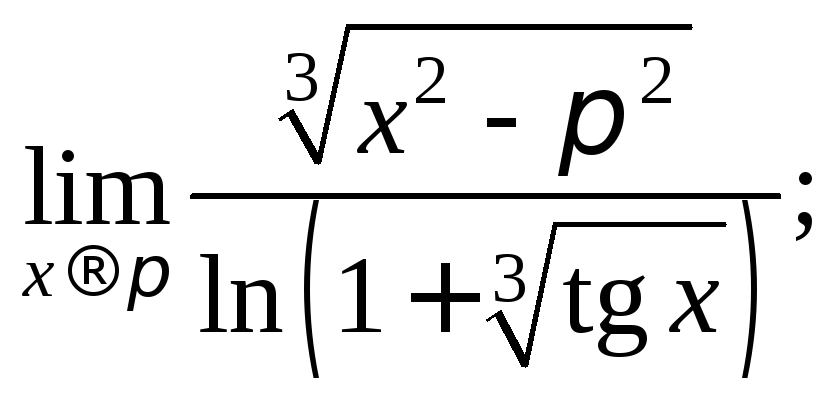 6)
6)![]()
7)
![]() 8)
8)
![]()
9)
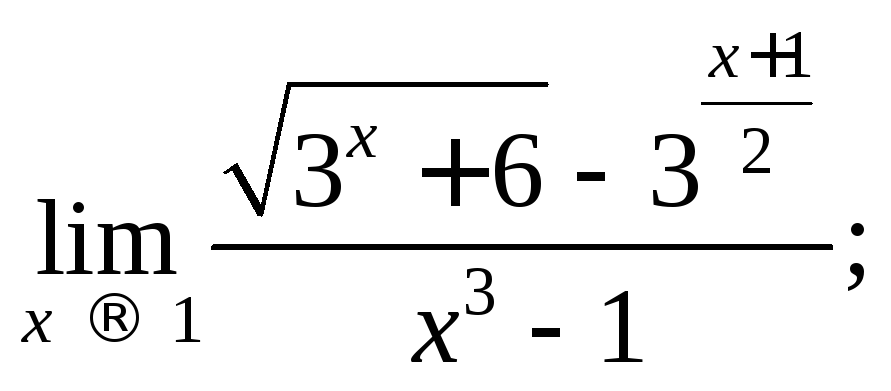 10)
10)
![]()
III уровень
3.1. Вычислите предел функции с помощью таблицы эквивалентности бесконечно малых двумя способами (производя замену переменной и без замены переменной):
1)
![]() 2)
2)![]()
3)
 4)
4)
![]()
3.2. Вычислите предел функции несколькими способами:
1)
![]()
2)
![]()
3.3. Вычислите предел функции:
1)
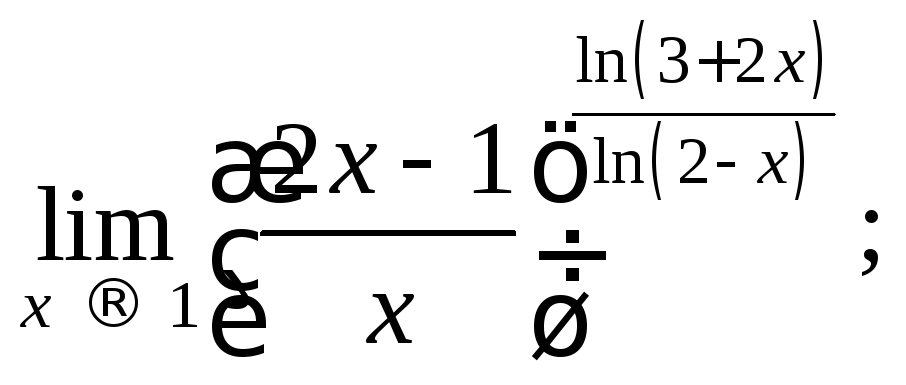 2)
2)
![]()
3)
![]() 4)
4)
![]()
16.4. Односторонние пределы. Асимптоты
графика функции
Левой (правой)
полуокрестностью точки х0
называется произвольный интервал
![]()
![]() где
где![]()
![]() слева (справа).
слева (справа).
Число А
называется
пределом
слева (справа) функции f(x)
в точке
х0,
если функция f(x)
определена в некоторой левой (правой)
полуокрестности точки
![]() и если для любого
и если для любого![]() существует
существует![]() такое, что для всехx,
удовлетворяющих условию
такое, что для всехx,
удовлетворяющих условию
![]() выполняется неравенство
выполняется неравенство
![]()
В этом случае
пишут:
![]()
Пределы слева и
справа называются односторонними
пределами.
Если
![]() то односторонние пределы обозначают
то односторонние пределы обозначают![]()
![]()
Функция f(x)
имеет предел в точке
![]() тогда
и только тогда, когда в этой точке
существуют оба односторонних предела,
равных между собой.
тогда
и только тогда, когда в этой точке
существуют оба односторонних предела,
равных между собой.
В этом случае их
общее значение является пределом функции
f(x)
в точке
![]()
![]()
Асимптота
графика
функции
![]() – это прямая линия, к которой неограниченно
приближается график данной функции,
когда его точка неограниченно удаляется
от начала координат.
– это прямая линия, к которой неограниченно
приближается график данной функции,
когда его точка неограниченно удаляется
от начала координат.
Различают горизонтальную, вертикальную и наклонную асимптоты.
Прямая
![]() называетсявертикальной
асимптотой
графика функции
называетсявертикальной
асимптотой
графика функции
![]() если
если![]() или
или![]()
В случае вертикальной
асимптоты
![]() функция является бесконечно большой в
точке
функция является бесконечно большой в
точке![]()
Прямая y
= b
называется горизонтальной
асимптотой
графика функции
![]() если
если![]()
Вертикальные асимптоты могут существовать у функций, которые определены не на всей числовой прямой, т. е. имеют разрыв второго рода.
Если областью определения функции является вся числовая прямая, то у функции нет вертикальных асимптот.
Прямая
![]() называетсянаклонной
асимптотой
графика функции
называетсянаклонной
асимптотой
графика функции
![]() при
при![]() если
если
![]()
Для нахождения коэффициентов k и b применяют следующие формулы:
![]() (16.25)
(16.25)
![]() (16.26)
(16.26)
Если хотя бы один
из пределов (16.25), (16.26) равен
![]() или не существует, то у функции наклонных
асимптот нет.
или не существует, то у функции наклонных
асимптот нет.
Если
![]()
![]() то прямая
то прямая![]() является горизонтальной асимптотой.
Заметим, что наклонных асимптот у функции
может быть не больше двух, а вертикальных
может быть сколько угодно.
является горизонтальной асимптотой.
Заметим, что наклонных асимптот у функции
может быть не больше двух, а вертикальных
может быть сколько угодно.
Пример 1. Найти односторонние пределы функции f(x) в точке х0:
1)
![]()
![]() 2)
2)![]()
![]()
Решение.
1) Вычислим
пределы функции в точке
![]() слева и справа, т. е.
слева и справа, т. е.![]() и
и![]()
Если
![]() то
то![]() значит
значит![]() Получаем
Получаем![]()
Если
![]() то
то![]() значит
значит![]() Получаем
Получаем![]()
2) При
![]() функция
задана формулой
функция
задана формулой![]() Поэтому
Поэтому
![]()
При
![]() функция задана формулой
функция задана формулой![]() т. е.
т. е.
![]()
Значит
![]()
Пример 2. С
помощью односторонних пределов показать,
что функция
![]() не имеет предела в точке
не имеет предела в точке![]()
Решение. При
![]() имеем
имеем![]() и функция принимает вид:
и функция принимает вид:
![]()
Поэтому
![]()
При
![]() имеем
имеем![]() и функцию
и функцию![]()
Поэтому
![]()
Получим, что оба
односторонних предела функции в точке
![]() существуют, однако они различны, поэтому
существуют, однако они различны, поэтому![]() не существует.
не существует.
Пример 3. Найти асимптоты графика функции:
1)
![]() 2)
2)![]()
Решение.
1) Вертикальных
асимптот данная функция не имеет, потому
что она определена для любых
![]() Для того чтобы найти горизонтальные
асимптоты, надо рассмотреть пределы
функции на бесконечности:
Для того чтобы найти горизонтальные
асимптоты, надо рассмотреть пределы
функции на бесконечности:
![]()
Получили, что
![]() – горизонтальная асимптота (ось0x).
– горизонтальная асимптота (ось0x).
Будем искать
наклонные асимптоты в виде функции
![]()
Согласно формулам (16.25) и (16.26), вычисляем:
![]()
Так как
![]() значит наклонных асимптот у графика
нет.
значит наклонных асимптот у графика
нет.
2) Так как при
![]() функция не определена, рассмотрим
функция не определена, рассмотрим
![]() и
и
![]()
Вычисляем:
![]()
![]()
Поэтому прямая
![]() является вертикальной асимптотой
графика функции.
является вертикальной асимптотой
графика функции.
Ищем горизонтальную асимптоту.
Вычисляем
![]()
это означает, что горизонтальных асимптот нет.
Выясним наличие наклонных асимптот. По формулам (16.25) и (16.26) находим:
![]()
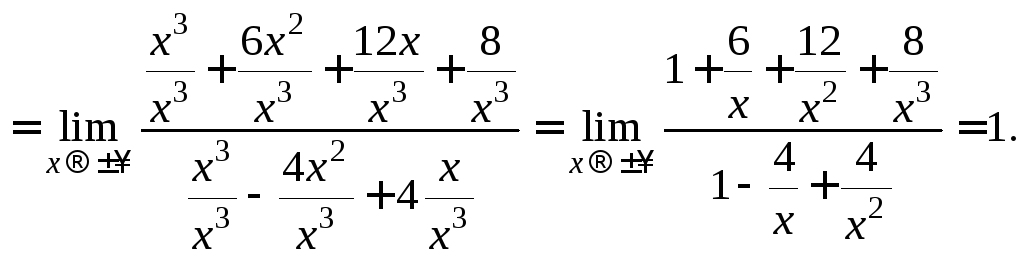


Приходим к выводу,
что
![]() – наклонная асимптота.
– наклонная асимптота.
Пример 4. Найти асимптоты графика функции:
1)
![]() 2)
2)![]()
Решение.
1) Областью определения D(y)
функции является то множество, на котором
выполняется неравенство
![]() Решив последнее неравенство, получим
что
Решив последнее неравенство, получим
что![]()
Определим
вертикальные асимптоты графика функции.
Рассмотрим поведение функции в окрестности
точки
![]() Функция определена только в левой
полуокрестности этой точки, поэтому
вычисляем левосторонний предел:
Функция определена только в левой
полуокрестности этой точки, поэтому
вычисляем левосторонний предел:
![]()
В окрестности
точки
![]() функция определена только справа,
поэтому в этой точке можем рассмотреть
правосторонний предел:
функция определена только справа,
поэтому в этой точке можем рассмотреть
правосторонний предел:
![]() .
.
Приходим к
заключению, что прямые
![]() и
и![]() являютсявертикальными
асимптотами графика функции. Горизонтальных
асимптот
нет, так как
являютсявертикальными
асимптотами графика функции. Горизонтальных
асимптот
нет, так как
![]()
Найдем наклонные асимптоты:
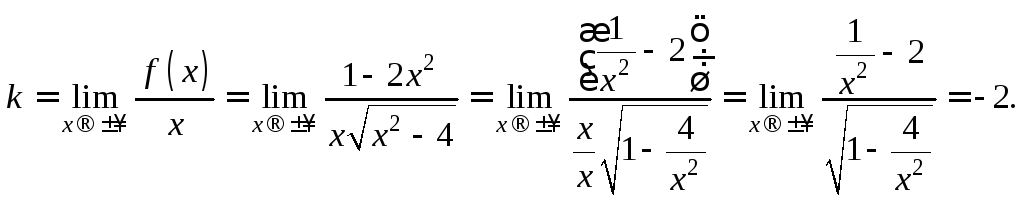
![]()
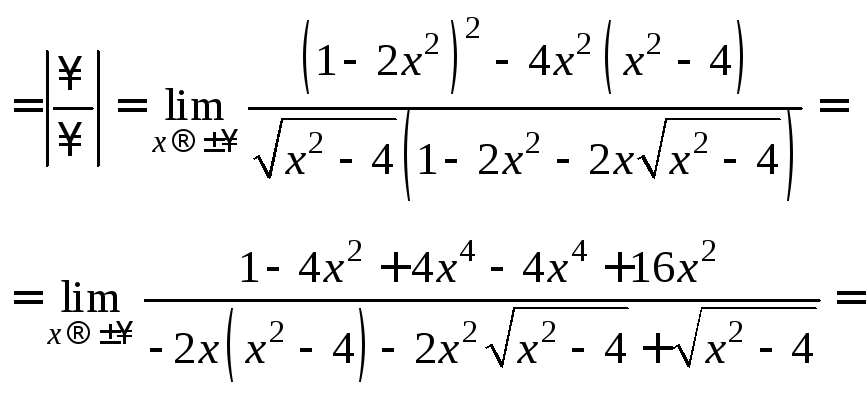
![]()
Таким образом,
![]() – наклонная асимптота.
– наклонная асимптота.
2) Функция определена
всюду на числовой прямой, кроме точки
![]() т. е.
т. е.![]() Рассмотрим
Рассмотрим
![]()
![]()
Прямая
![]() – вертикальная асимптота.
– вертикальная асимптота.
Найдем горизонтальные асимптоты:
![]()
![]()
Получаем, что
прямая
![]() является горизонтальной асимптотой
при
является горизонтальной асимптотой
при![]() а прямая
а прямая![]() – горизонтальная асимптота при
– горизонтальная асимптота при![]()
Ищем наклонные асимптоты:

Наклонных асимптот нет.
Задания
