18.6. Частные производные и дифференциалы

высших порядков

Частными производными второго порядкафункцииназываются частные производные от ее частных производных первого порядка:

(18.21)

(18.22)

(18.23)

(18.24)

Частные производные (18.21–18.24) обозначают также (соответственно)

Аналогично определяются частные производные третьего, четвертого и высших порядков.

В частности,

Подобным образом определяются производные высшего порядка функции трех и более переменных.

Частная производная второго порядка и выше, взятая по различным переменным, называется смешаннойчастнойпроизводной.

Если частные производные высшего порядка непрерывны, то смешанные производные одного порядка не зависят от порядка дифференцирования, например,

Дифференциал второго порядкафункцииопределяется формулой

(18.25)

Аналогично определяются дифференциалы третьего и высших порядков.

Справедлива формула

(18.26)

Если функция имеет непрерывные частные производные, и переменныехиуявляются независимыми, то дифференциалы второго и третьего порядков вычисляются по формулам:

(18.27)

(18.28)

Для всякого формула вычисления дифференциала порядкапо форме записи аналогична формуле бинома Ньютона:

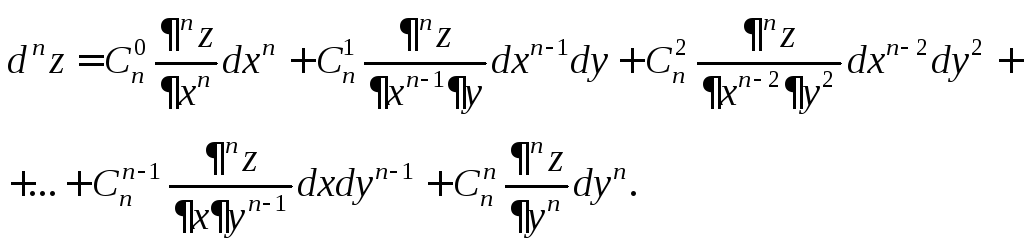(18.29)

Пример 1. Вычислить частные производные второго порядка функции:

1) 2)в точке

Решение. 1) Найдем частные производные первого порядка:

Далее дифференцируем полученные производные по x и по y каждую:

2) Находим частные производные первого порядка:

Полученные равенства дифференцируем еще раз по x и по y:

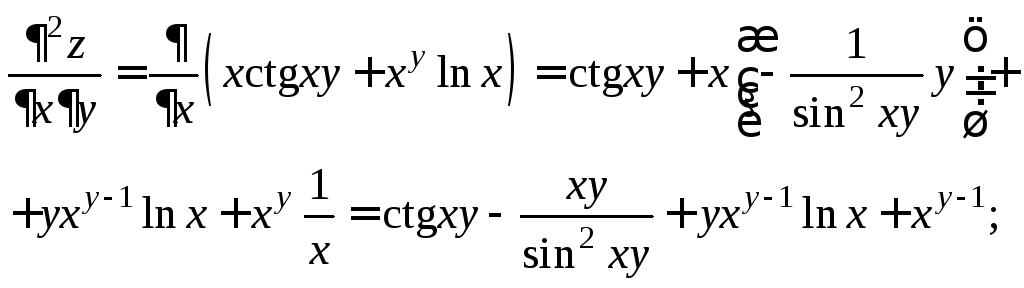
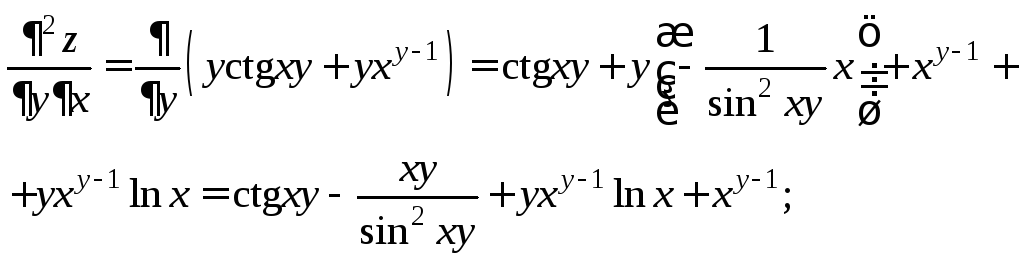
Найдем значения частных производных в точке

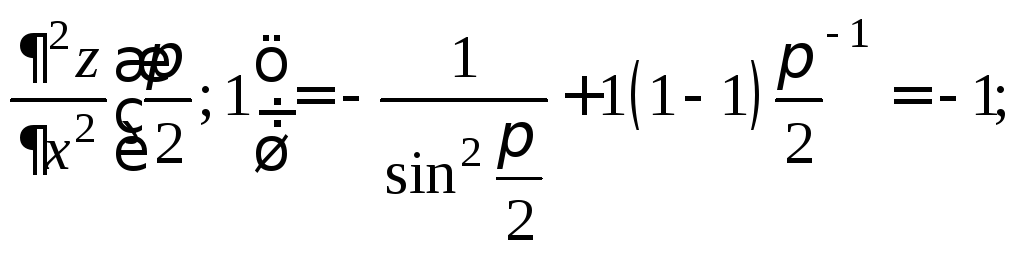
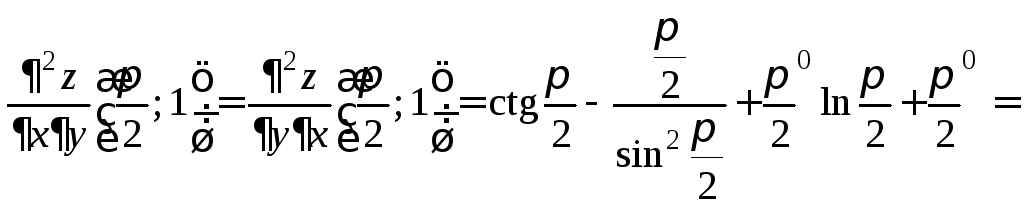
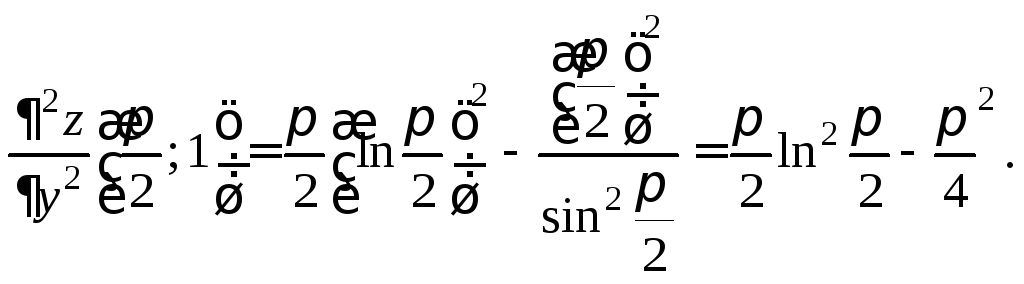
Пример 2. Найти частную производную функции

Решение. Найдем частную производную 1-го порядка

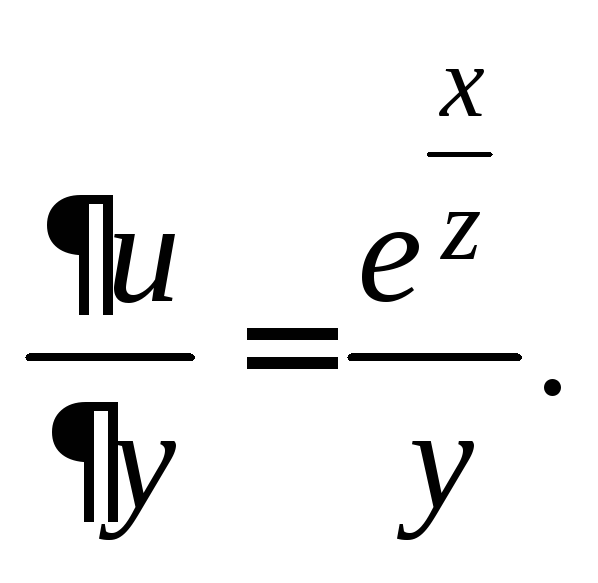
Продифференцировав полученное равенство дважды по z, получим:

Дифференцируем последнее равенство дважды по х:

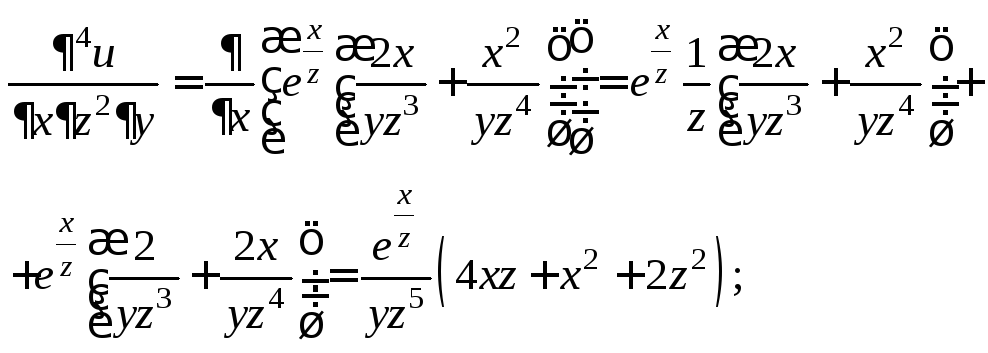
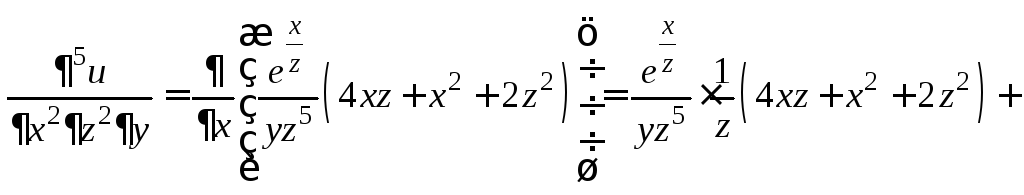
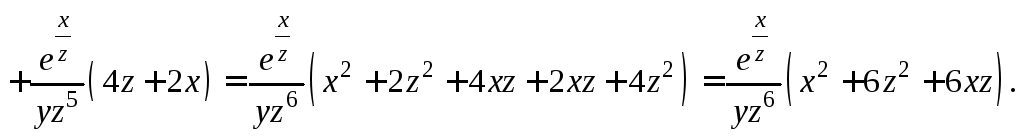
Пример 3. Найти дифференциал четвертого порядка функции в точке

Решение. По формуле (18.29) имеем:

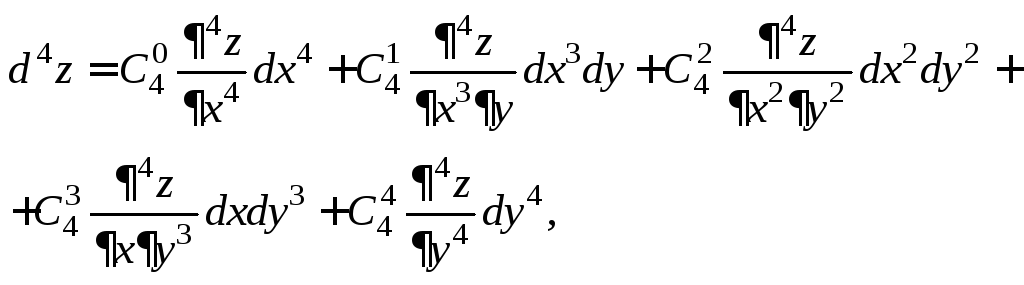
где – биномиальные коэффициенты, которые найдем по формуле

или по треугольнику Паскаля.

Формула вычисления принимает вид:

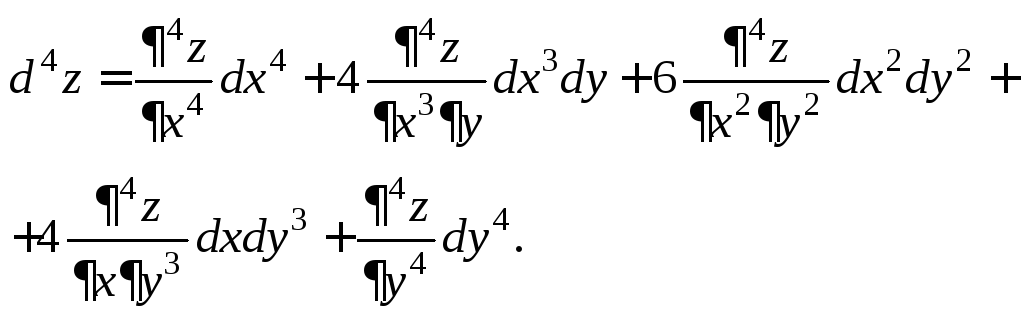(18.30)

Найдем частные производные:

Вычислим значения частных производных в точке

Подставляя все значения в формулу (18.30), получим:

Задания

I уровень

1.1. Вычислите частные производные второго порядка функции:

1) 2)

3) 4)

5) в точке

6) в точке

1.2.Найдите производнуюфункции

1.3.Найдите производнуюфункции

1.4.Вычислите дифференциалы третьего порядка функциив точкеМ₀:

1)

2)

II уровень

2.1.Найдите частные производные указанного порядка:

1) если

2) если

3) если

4) если

5) если

6) если

2.2.Найдите дифференциалы второго порядка функцииzв точке

1) 2)

2.3.Найдите дифференциалы указанного порядка функции:

1) если2)если

3) если4)если

2.4.Докажите, что для функциисправедливо равенствоесли

III уровень

3.1.Докажите, что указанная функцияимеет в точкесмешанные частные производные второго порядка, но при этом

1)

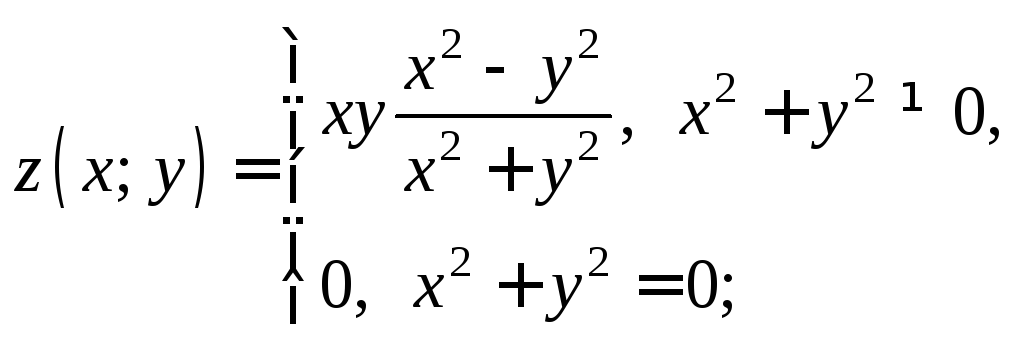
2)

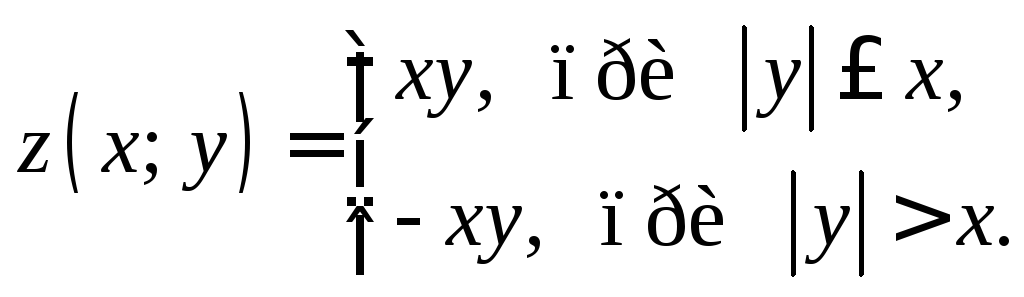
3.2.Найдите второй дифференциал функциив точкеесли– дифференцируемые функции:

1)

2)

3)

3.3.Докажите, что функция(а,х₀– числа) удовлетворяет уравнению теплопроводности

3.4.Докажите, что произвольные дважды дифференцируемые функцииfиgудовлетворяют уравнениям:

1)

2)

3)

3.5.Найдите решениеуравнения:

1) удовлетворяющее условиям

2) удовлетворяющее условиям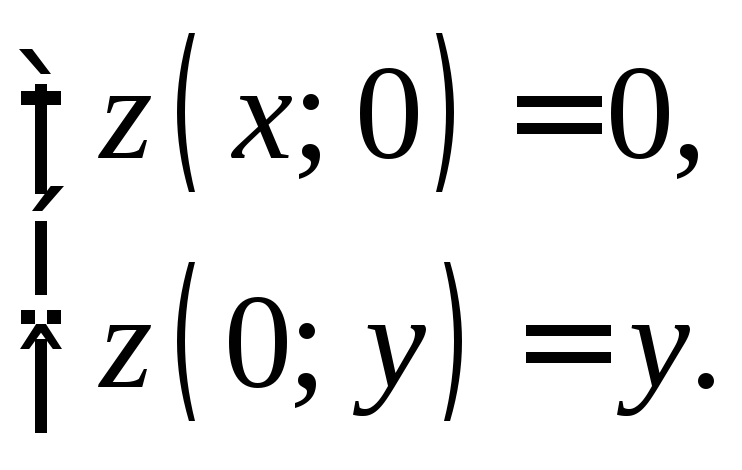

3.6.Проверьте равенства:

1) 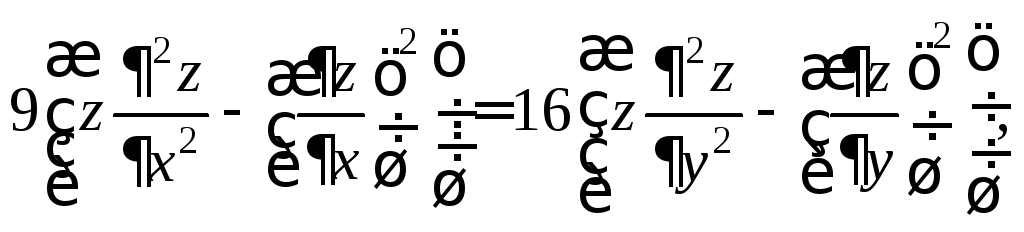если

2) если