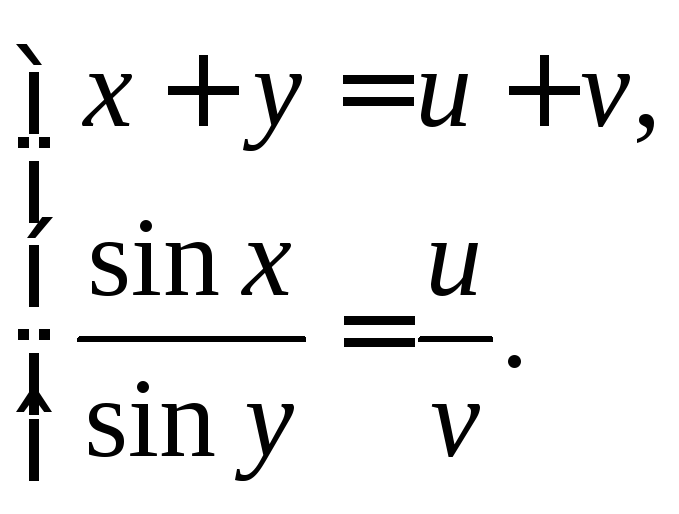I уровень

1.1.Найдитефункции, при

1) где

2) где

1.2.Найдитефункциигде

1.3.Найдите частные производныеи

1) где

2) где

3) где

1.4.Найдите производнуюфункции:

1) где

2) где

II уровень

2.1.Найдите двумя способамиифункции:

1) где

2) где

3) где

2.2.Найдитефункцииuв точке

1) где

2) где

3) где

2.3. Найдите частные производные ифункции:

1) где

2) где

2.4.Покажите, что функцияудовлетворяет уравнению

III уровень

3.1.Найдите частные производныеифункции в точке

1) гдеN₀(1; 1; 1);

2) где

3.2.Вычислите определитель:

1) 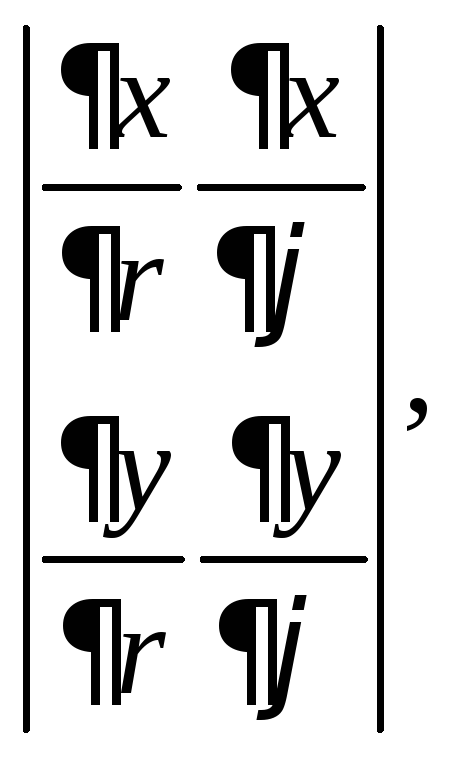если

2) если

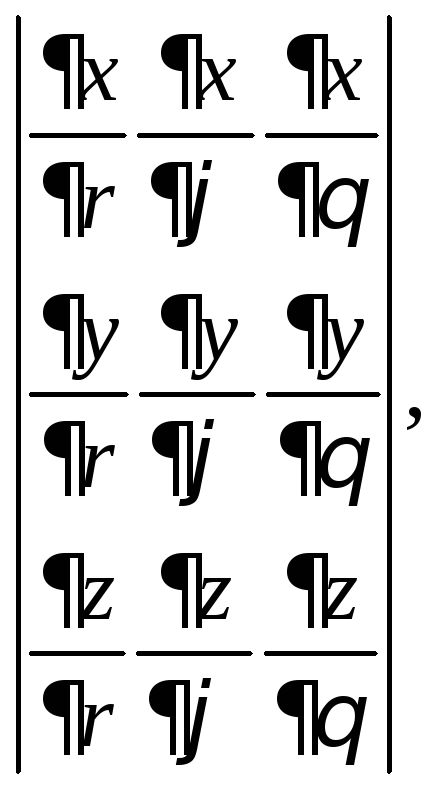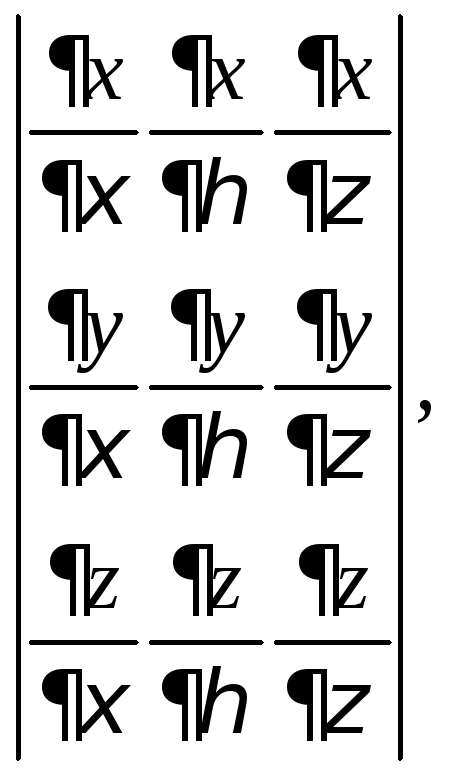3) если

3.3.Проверьте равенства:

1) если

2) если

3) если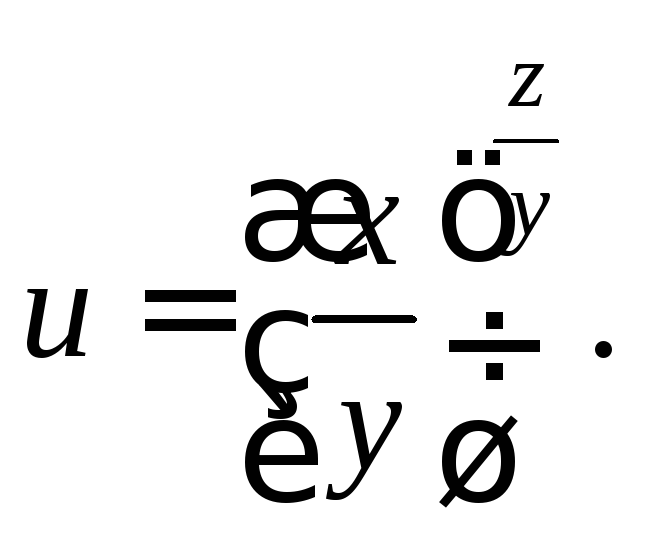

18.4. Дифференцирование неявных функций

Допустим, что функция задана неявно уравнением

(18.12)

и требуется найти

1-й способ. Если практически возможно, из (18.12) выражают явночерези дифференцируют.

2-й способ.Дифференцируют уравнение (18.12), считаяи выражают затем

3-й способ.Используют формулу

(18.13)

если

Способы 1–2 были рассмотрены в теории дифференцирования функции одной переменной и не всегда являются рациональными.

Производные неявной функции порядка выше первого находят последовательным дифференцированием формулы (18.13), учитывая, чтоy– функция отx.

Для нахождения частных производных функции заданной неявно уравнением

(18.14)

используют формулы

(18.15)

при условии, что эти производные существуют и

Пример 1. Для функции заданной неявно уравнениемнайтивсеми возможными способами.

Решение. Используем 1-й способ. Выражаем y через x и дифференцируем по x:

Таким образом,

Используем 2-й способ. Продифференцируем по x заданное уравнение, считая

Отсюда выражаем

или

Используем 3-й способ. Применим формулу (18.13):

По формуле (18.13) получаем:

или

Вывод: способы 2 и 3 оказались наиболее рациональными.

Пример 2. Найти функциизаданной неявно уравнением

Решение. Используем 3-й способ.

По формуле (18.13) получаем:

Таким образом,

Пример 3. Найти в точкефункциизаданной неявно уравнением

Решение. Вычислим по формуле (18.13):

Пусть Вычислимподставивв исходное уравнение:

Тогда

Пример 4. Найти функциизаданной неявно уравнениемесли

Решение. Воспользуемся формулой (18.15) для функции

Вычисляем:

Тогда по формуле (18.15) имеем:

Для заданной точки найдем соответствующее значениеДля этого подставимв уравнение, которое задает неявно функциюz: ПолучаемПодставив значенияв выраженияиполучим

Задания

I уровень

1.1.Найдитефункции:

1) 2)

3) 4)

5) 6)

7) 8)

1.2.Найдитефункцииz, заданной неявно уравнением:

1) 2)

3) 4)

II уровень

2.1.Найдитефункции, если:

1) 2)

3) 4)

2.2.Дано уравнениеНайдитедвумя способами.

2.3.Дано уравнение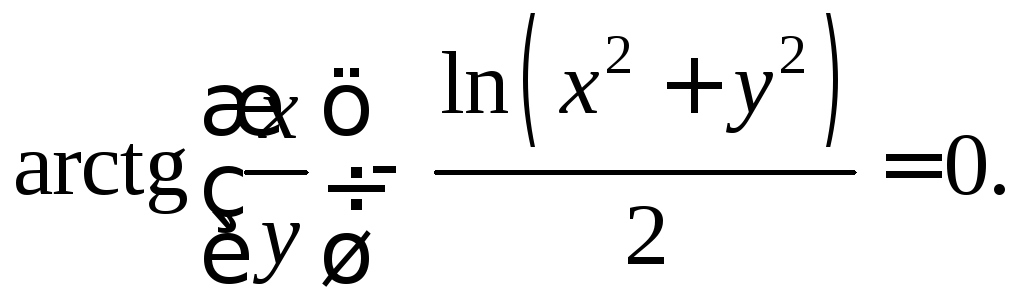Найдитеесли

2.4.Найдите частные производныеифункции:

1)

2)

3)

2.5.Найдите частные производные функции:

1) 2)

3) 4)

III уровень

3.1.Найдите производные функцийв точкеесли функции заданы системой уравнений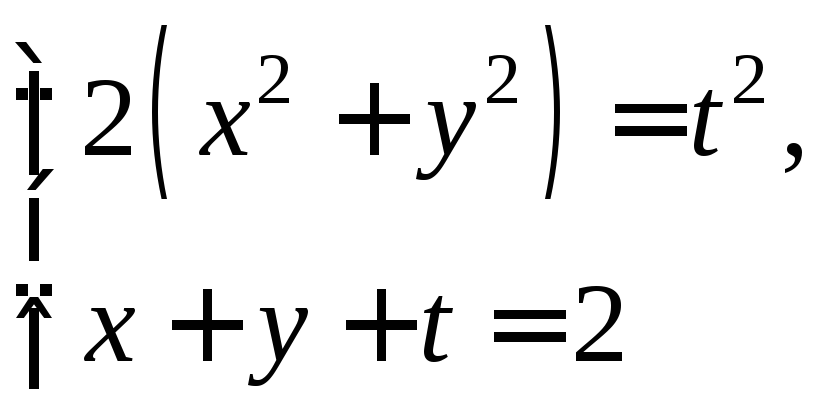и удовлетворяют условиям

3.2.Найдите производныенеявных функцийудовлетворяющих условиями заданных системой уравнений:

1) 2)

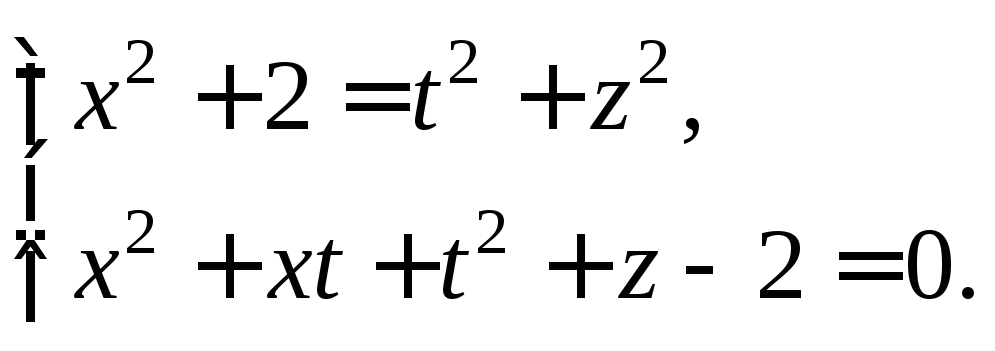
3.3.Докажите, что неявная функцияопределяемая уравнениемудовлетворяет уравнению

3.4.Докажите, что неявная функцияопределяемая уравнениемявляется решением уравнения

3.5.Докажите, что неявная функциязаданная уравнениемудовлетворяет уравнению

3.6.Найдите дифференциал функциизаданной уравнениемв точкеи удовлетворяющей условию

3.7.Найдите дифференциалы функцийизаданных системой уравнений