I уровень

1.1.Найдите точку пересечения прямойс плоскостьюили установите их параллельность:

1)

2)

3)

4)

5)

1.2.Найдите угол между прямой и плоскостью:

1) и

2) и

3) и

1.3.Составьте уравнение плоскости, проходящей через начало координат и прямую

II уровень

2.1.Определите, при каком значенииmпрямая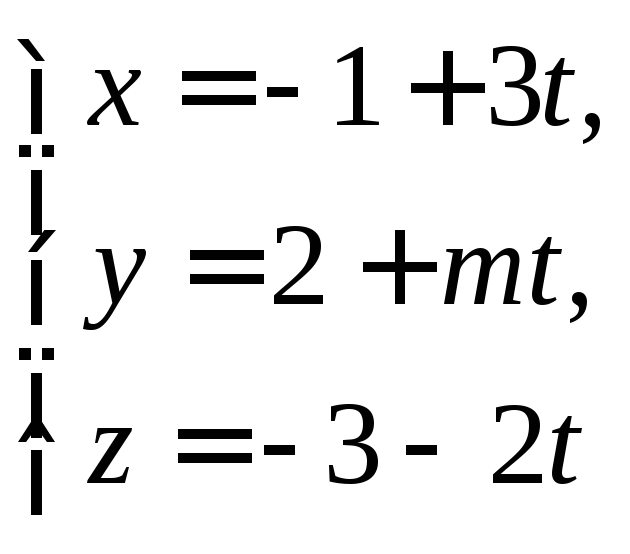не имеет с плоскостьюобщих точек.

2.2.Найдите, при каких значенияхmиnпрямаялежит в плоскости

2.3.Найдите, при каких значенияхmиnпрямая перпендикулярна плоскости

2.4.Составьте уравнение плоскости, проходящей через прямуюпараллельно прямой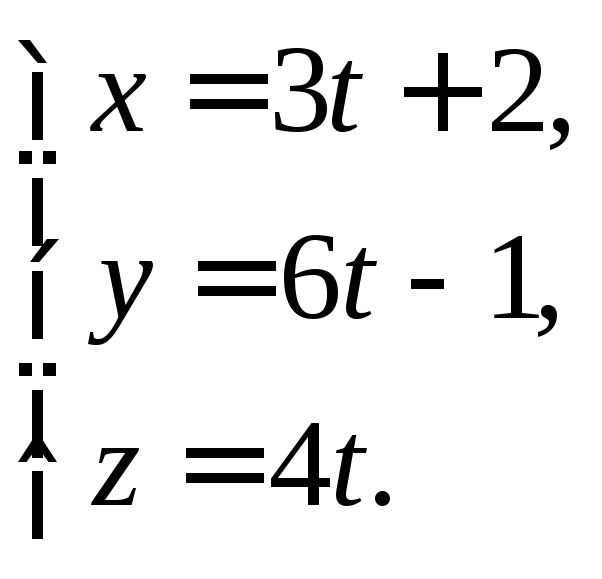

2.5.Составьте уравнение плоскости, проходящей через осьOzпараллельно прямой

2.6.Составьте уравнение прямой, проходящей через точкуи перпендикулярной плоскости

2.7.Найдите проекцию точкина плоскость

2.8.Найдите точку, симметричную точкеотносительно плоскости

2.9.Напишите уравнение плоскости, проходящей через точкуперпендикулярно прямой

2.10.Составьте уравнение плоскости, проходящей через прямуюпараллельно вектору

III уровень

3.1.Составьте параметрические уравнения прямой, которая проходит через точкупараллельно плоскостии пересекает прямую

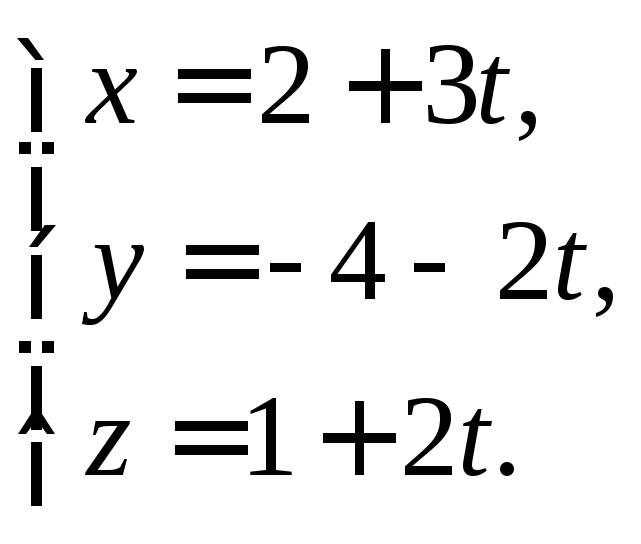
3.2.Найдите проекцию прямойLна плоскостьесли она задана уравнениями:

1) 2)

3.3.Найдите основание перпендикуляра, проведенного из точкик прямой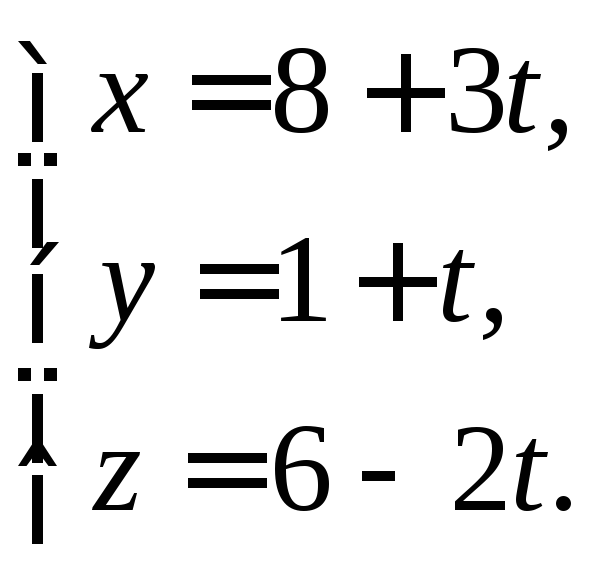

3.4. Найдите точку, симметричную точкеотносительно прямой

3.5.Составьте уравнение плоскости, перпендикулярной плоскостии:

1) пересекающей ее по прямой, лежащей в плоскости Oxy;

2) проходящей через прямую

3.6.Составьте уравнение прямой, проходящей через точку пересечения плоскостис прямой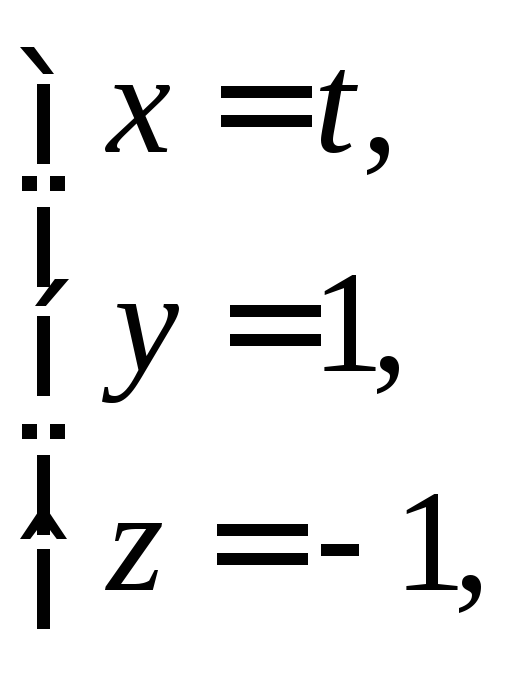при условии, что искомая прямая принадлежит заданной плоскости и перпендикулярна заданной прямой.

15.4. Поверхности второго порядка

Поверхностью второго порядканазывается поверхностьS, общее уравнение которой в декартовой прямоугольной системе координат имеет вид:

(15.22)

где коэффициенты при одночленах второй степени одновременно не равны нулю.

Существует девять типов невырожденных поверхностей, уравнения которых с помощью преобразования координат могут быть приведены к одному из следующих видов. Эти уравнения определяют тип поверхности и называются каноническими уравнениями.

1. Эллипсоид:(рис. 15.1).

Рис. 15.1

2. Конус второго порядка:(рис. 15.2).

Рис. 15.2

3. Гиперболоиды

1) однополостный: (рис. 15.3);

2) двуполостный: (рис. 15.4).

Рис. 15.3 Рис. 15.4

4. Параболоиды

1) эллиптический: (рис. 15.5);

2) гиперболический: (рис.15.6).

Рис. 15.5 Рис. 15.6

5. Цилиндры

1) эллиптический: (рис. 15.7);

2) гиперболический: (рис. 15.8);

Рис. 15.7 Рис. 15.8

3) параболический:(рис. 15.9).

Рис. 15.9

Основным методом исследования формы поверхности является метод параллельных сечений, который состоит в следующем. Поверхность пересекается координатными плоскостями и им параллельными, а затем на основании вида полученных в сечениях линий делается вывод о типе поверхности. Таким образом можно изучать основные геометрические свойства невырожденных поверхностей второго порядка на основе их канонических уравнений.

При этом, когда в общем уравнении поверхности коэффициенты приведение к каноническому виду осуществляется с помощью метода выделения полных квадратов.

В определенных случаях уравнение (15.22) поверхности может быть приведено к уравнениям, задающим, так называемые, вырожденные поверхности. Приведем примеры таких случаев:

–пустое множество точек (мнимый эллипсоид);

–точка (0, 0, 0);

–пустое множество точек (мнимый эллиптический цилиндр);

–прямая (ось Oz);

–пара пересекающихся плоскостей;

–пара параллельных плоскостей;

–пустое множество точек;

–плоскость (пара совпадающих плоскостей).

Пример 1. Привести уравнение к каноническому виду и определить тип поверхности, которую оно задает:

1)

2)

3)

4)

Решение. 1) Воспользуемся методом выделения полных квадратов.

Преобразуем левую часть уравнения:

Значит, заданное уравнение равносильно уравнению

или

Имеем уравнение однополостного гиперболоида, центр которого находится в точке (–1, 1, 2). Его ось симметрии – прямая, параллельная оси Oz и проходящая через точку (–1, 1, 2).

2) Поскольку

то заданное уравнение равносильно уравнению

или что приводит окончательно к уравнению гиперболического параболоидасмещенного в точку (–1, 0, 1).

3) Выделяем полные квадраты в выражении, стоящем в левой части уравнения:

Поэтому заданное уравнение принимает вид:

или (после деления на 36)

Это уравнение эллипсоида с центром в точке (3, – 1, 2).

4. Методом выделения полных квадратов уравнение приводится к уравнению

т. е.

Почленное деление на 36 дает:

Это уравнение эллиптического цилиндра, смещенного в точку (–2, 5, 0).

Пример 2. Исследовать поверхность методом сечений и построить ее:

Решение. Для исследования геометрических свойств и формы поверхности используем метод сечений.

Определим сечение поверхности плоскостями гдепараллельными координатной плоскостиOxy:

Очевидно, что это кривые, проекции которых на ось Oxy задаются уравнением

(15.23)

Уравнение (15.23) при не имеет решений относительноЭто означает, что соответствующее сечение есть пустое множество точек, а значит, рассматриваемая поверхность целиком расположена ниже плоскостиПриуравнение (15.23) определяет эллипс

с полуосями ивырождающийся в точку (0, 0, 1) приЗаметим, что все эллипсы, которые получаются в сечениях поверхности плоскостямиподобны между собой, причем с уменьшениемh их полуоси неограниченно монотонно возрастают.

Дальнейшее уточнение формы можно получить, рассматривая сечения координатными плоскостями Oxz и Oyz:

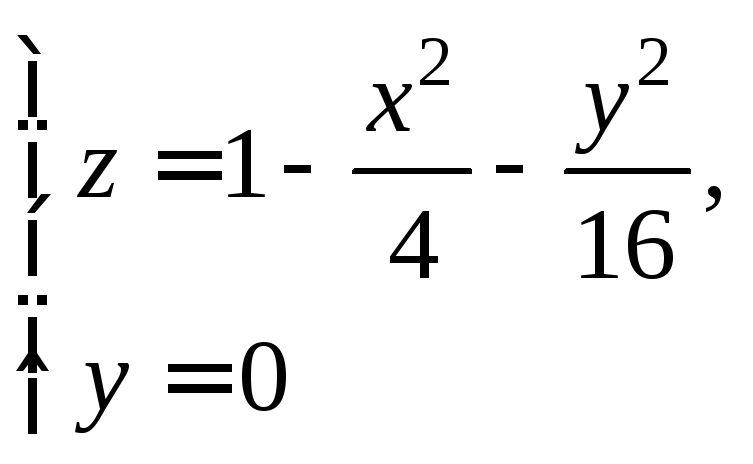и

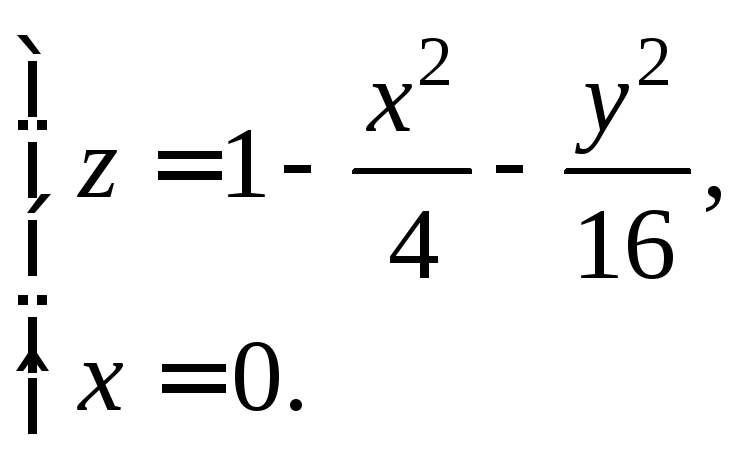
В первом случае имеем кривую т. е. параболу с параметромвершиной в точкеи ветвями, направленными в отрицательную сторону осиOz. Во втором – параболу с параметромвершиной в точкеи аналогичным направлением ветвей.

Выполненное исследование позволяет построить заданную поверхность (рис. 15.10). Это эллиптический параболоид с вершиной в точке (0, 0, 1), направленный в сторону убывания значенийz с осью симметрии Oz.

Рис. 15.10

Пример 3. Построить тело, ограниченное поверхностями

Решение. Уравнение задает плоскость. Перейдя к уравнению плоскости «в отрезках», получим:

т. е. плоскость пересекает координатные оси в точках (3, 0, 0), (0, 3, 0) и (0, 0, 3) соответственно.

Уравнение задает круговой цилиндр, осью которого служитOz. Уравнение определяет координатную плоскостьOxy.

Сделаем рисунок тела (рис. 15.11, 15.12), ограниченного заданными поверхностями.

Рис. 15.11 Рис. 15.12

Задания