SMMiF_bsuir

11

www.studhelp.info

считается очень легко.

пº4. Для матриц A = (aij ) и B = (bij )

порядка m × n можно было бы ввести

расстояние в евклидовой метрике:

fo

m

n

r(A, B) = åå(aij - bij )2 .

n

i=1 j=1

смотреть более простые метрики, например, метрику Чебышёва:

r (

,

) = max

| a

- b | .

i

x

y

ij

1

1≤i≤m

ij

.

1≤ j≤n

L

Для анализа линейных систем часто оперируют нормами матриц. Их можно

определить так:

E

P

æ

n

ö

æ m

ö

A

ç

÷

,

= max

ç

å| aij |

÷

.

1 = maxç

å| aij |÷

A

2

UDH

÷

1≤i≤mè j=1

ø

1≤ j≤mç

A

A

è i=1

ø

1

и

2 – это соответственно максимум среди сумм абсолютных величин

элементов строк или столбцов матрицы А. Например,

A

=

æ1

2

ö

= max{3,8} = 8 ;

A

=

æ1

2

ö

= max{4,7} = 7 .

ç

÷

ç

÷

ç

÷

ç

÷

1

è- 3 5

ø

T

2

è- 3 5

ø

.пº5. На множестве C[a,b] непрерывных на отрезке [a,b] функций расстоя-

ние ρ между элементами f (x) и ϕ(x) вычисляется так:

S

ρ( f ,ϕ) = max

.

.

x[a,b]

уклонение АВ – самый большой зазор между графиками функций f и ϕ на

[a,b] .

А

пº6. C n [a, b] – это множество

ϕ(x)

ρ( f ,ϕ)

функций, имеющих на отрезке [a,b]

В

непрерывные производные

f (x)

до n -го порядка включительно.

а

x0

b

n

Рис. 1.1.

wwwНа C [a, b] метрическая функция

ного компьютера

на другой,

обычно

записывается в виде

вектора

(x1, x2,...,xn) , где

xi равно либо 0, либо 1. Рассмотрим линейное пространство

x

Ln векторов

над полем F2 (0;1)

двух чисел – 0 и 1. Операции Å и Ä в этом

x

поле таковы:

1 Å 0 = 1,

0 Ä1 = 0,

fo

0 Å 0 = 0,

0 Ä 0 = 0,

in

0 Å1 = 1,

1 Ä 0 = 0,

1 Å1 = 0,

1 Ä1 =1.

В роли числа, противоположного к 1, выступает 1.

.

L

Например,

x

(0,1,0,0,0,0,0,1)

– вектор из L8 , а

x

(1,0,1,1) – вектор из L4 .

E

Расстояние между

x

и y обозначается

dist(x, y) (сокращенноP

от англ. dis-

tance), равно числу различий в координатах векторов

и

и называется мет-

x

y

рикой Хэмминга.

UDH

Пусть, например,

=(1,0,1,1),

=(0,1,1,0). У этих векторов третьи координа-

x

y

ты одинаковы,

а

остальные

различны.

Поэтому

dist(

,

) = 3 .

Если же

x

y

=(1,0,0,0,0,0,1,0),

=(0,1,1,0,0,1,0,1), то dist(

,

) = 5 .

x

y

x

y

Можно убедиться в том, что аксиомы 1º - 3º метрического пространства вы-

полняются для множества Ln и метрики Хэмминга.

Выясним, чему равна норма

x

вектора

x

.

x

– это, фактически, норма раз-

S

ности вектора

x

и нулевого вектора или,

другими словами, это расстояние от

.

вектора

x

до нулевогоTвектора. Поэтому

x

равна числу ненулевых координат

www

вектора x . Например,

x(0,1,0,1,1,1,0,0,0)

= 4 .

пº8. Пусть V ={

(xn),

(xn),...} – множество ограниченных последовательно-

x

y

стей:

(xn ) = x1, x2,..., xn,...;

|≤ X , i = 1,2,..., X R;

| xi

x

( yn ) = y1, y2 ,..., yn ,....;| yi |≤ Y,i = 1,2,...,Y R.

y

На V метрическая функция вводится так:

ρ(

,

) = max

| xn - yn |,

,

ÎV .

x

y

x

y

n=1,2,...

13

www.studhelp.info

ляющемуся элементом этого пространства.

fo

Рассмотрим простой пример.

Пусть X = (a,b) – это интервал, а метрика

x

y

ρ(x, y) =| x − y |

– обычное расстояние

b

а

между точками

x и y на прямой.

Рассмотрим какую-нибудь последовательность x1, x2

,..., xn ,

, сходящуюся к

n

i

.

пространство, надо дополнить X концами интервала, т.е. точками а и b. Итак,

если X = [a,b], то (X , ρ)

– полное метрическое пространствоP.

L

1.6. Пространство Гильберта

E

В параграфе 1.3 была введена операция скалярного произведения в действи-

*

*

UDH

стве

H задана

операция скалярного произведения, если каждой паре векторов

T

x

и

y из H сопоставляется комплексное число

(x, y) так, что

"x, y, x1, x2 Î H

и α С выполняются аксиомы:

S

1º. (x, y) = (y, x) (знак означает комплексное сопряжение);

.

, y) + (x2 , y);

2º. (x1 Å x2 , y) = (x1

www

= α(x, y) ;

3º. (α Ä x, y)

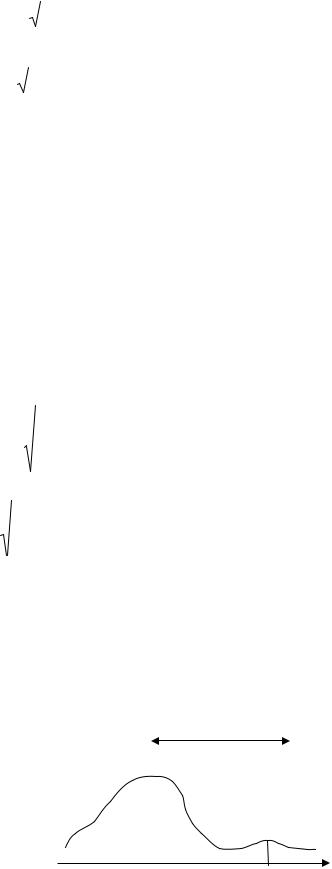
14

www.studhelp.info

=

(

,

) ;

x

x

x

2) расстояние между векторами

и

:

x

y

r(

,

) =

-

=

(

-

,

-

) .

(1.2)

x

y

x

y

x

y

x

y

Метрика, задаваемая формулой (1.2), называется метрикой, порожденной

скалярным произведением.

Определение 1.12. Комплексное линейное пространство H называется про-

fo

странством Гильберта, если выполнены следующие условия: 1) на H задано

скалярное произведение; 2)

H – полное метрическое пространство относитель-

но метрики, порожденной скалярным произведением.

n

Многие сигналы, возникающие в радиотехнике, принадлежат пространству

.

L2 (−∞, ∞) . Через L2 (−∞, ∞) в математике принято обозначать множество

функций,

интегрируемых

с

квадратом

на интервалеi(−∞, ∞) , т.е.

L2 (−∞, ∞) = {f (x), g(x),...} такое множество,

что для

f (x) L2 (−∞, ∞) спра-

ведливо условие ò−∞∞ f 2 (x)dx <¥ .

L

ò

E

P

Если s(t) L2 (−∞, ∞), то

UDH

+∞

s(t)

=

s2(t)dt

в случае вещественного сигнала и

−∞

+∞

s(t)

=

ò s(t) × s * (t) dt ,

где s *(t)

T

−∞

s(t) , в случае комплексного

– комплексно-сопряженное значение к

сигнала s(t) .

S

s

Квадрат нормы сигнала s(t)

носит название «энергии» сигнала и обознача-

ется Es :

.

www

E

=

s(t)

2.

R =1 см

Именно такая энергия выделяется в

резисторе с сопротивлением 1 ом,

s(t)

если на его зажимы подано напряжение s(t) .