Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Институт информационных технологий БГУИР

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

SMMiF_bsuir

.pdf

Скачиваний:

Добавлен:

24.02.2016

Размер:

956.88 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 125 6 7 8 9 10 11 12 > Следующая >>>

41	www.studhelp.info

Напомним, что для абсолютно интегрируемых функций существуют прямое и обратное преобразования Фурье. Прямое преобразование Фурье F(ω) функ-

ции f (t) задается формулой

∞

F(ω) = ò f (t)e−i2πωt dt

(4.1)

−∞

и иногда еще называется спектральной функцией интеграла Фурье.

Зная функцию F(ω) , можно восстановить сигнал

f (t) с помощью обратного

преобразования Фурье:

∞

f (t) = ò F(ω)ei2πωt dω .

(4.2)

−∞

В дальнейшем будем использовать запись f (t) ↔ F(ω) , означающую, что

функция F(ω) является прямым преобразованием Фурье сигналаif (t) .

Легко заметить, что операторы (4.1) и (4.2) линейны:

если

f1(t) ↔ F1(ω) ,

то

f 2 (t) ↔ F2 (ω),

UDH

+ c2F2 (ω) ,

c1 f1

(t) + c2 f

2 (t) ↔ c1F1(ω)

где c1,c2 – произвольные числа.

Задача 1. Дано:

f (t) ↔ F(ω) .

Найти спектральную функцию сигнала F(t).

D По определению спектральной функции для сигнала F(t) имеем:

+ ¥

F(t) e- i2pwt dt =

введем

замену

w = -w1

- ¥

(4.2)

- ¥

+ ¥

www

ò F(t) ei2pw1t dt = f (w ) = f (-w).

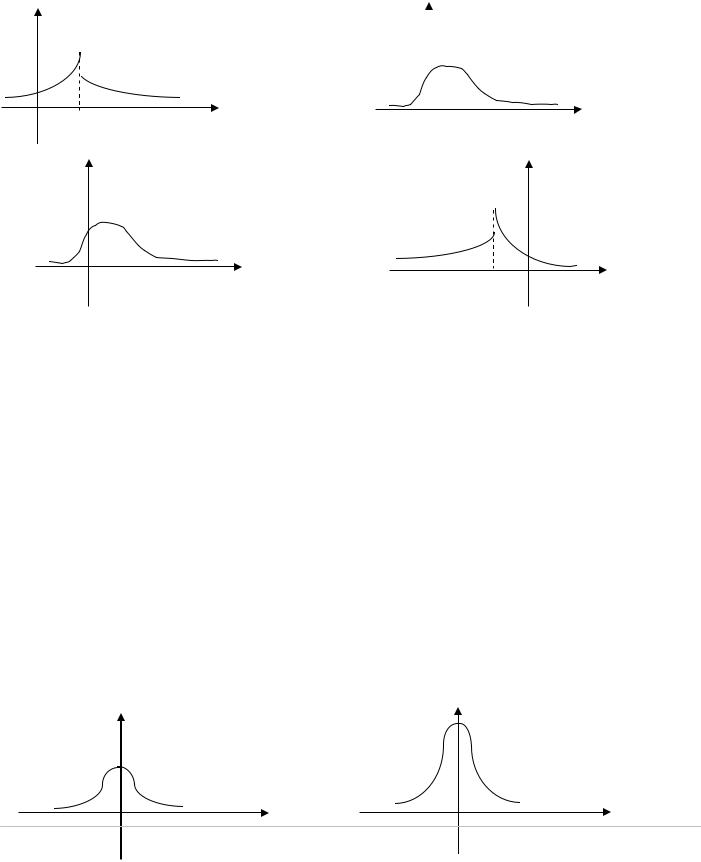
Итак, мы вывели очень важное свойство дуальности соответствия: если

f (t) ↔ F(ω) ,

то

F(t) ↔ f (−ω) .

Рассмотрим геометрический смысл этого свойства:

42	www.studhelp.info

если

f(t)

F(ω)

↔

0	t0		t			0			ω
то	F(t)								fo
то	F(t)							(−ω)
								n
			↔				i
			↔				.0
	0		t				.0
	0		t				-t	0	ω
						L			▲
Задача 2. Доказать:					E		P
а) если f (−t) ≡ f (t), то F(−ω) = F(ω);					E
а) если f (−t) ≡ f (t), то F(−ω) = F(ω);
б) если f (−t) ≡ − f (t) , то F(−ω) = −F(ω) .
			UDH
Из (4.1) с учетом формулы Эйлера следует, что
		+∞		+∞
	F(ω) = ò f (t) cos 2πωt dt − i ò f (t) sin 2πωt dt = a(ω) − ib(ω) .
		−∞		−∞
		144424443		144424443
			a(ω)		b(ω)
Заметим, что F(−ω) = a(ω) + ib(ω).
		T				∞
а)	Пусть f(t)	– четная функция. Тогда a(ω) = 2ò f (t) cos 2πωt dt как интеграл
		S				0
						0

от четной функции по симметричному интервалу интегрирования и b(ω) = 0

	.			▲
Утверждение пункта б) доказывается аналогично.				▲
Если говорить образно, то справедливы такие картины соответствия:
а)		f		F
www		f(t)		F(ω)
www		0	t	0	ω

как интеграл от нечетной функции по симметричному интервалу. Следователь-

но, F(−ω) = F(ω)

www.studhelp.info

б)

f(t)

F(ω)

▲

Задача 3. Доказать справедливость утверждения:

если

f (t) ↔ F(ω) ,

то

f '(t) ↔ i2πωF(ω) .

интегрируем

по

частям :

∞

∞ +

u = e−i2πωt ;

dv = f '(t)dt;

= f (t)e−i2πωt

f ' (t) ↔ ò f '(t)e−i2πωt dt =

−∞

du = −i2πωe−i2πωt dt; v = fP(t)

−∞

первое

слагаемое

суммы равно нулю,

так

как

∞

f (−∞) = f (∞) = 0

из− за

∞

+ i2πω ò f (t)e−i2πωtdt =

= i2πωF(ω).

−∞

условия

ò|

f (t) | dt = Q < +∞,

а второе

−∞

слагаемое

преобразуем

по

формуле (4.1)

▲

Так как операция интегрирования обратна операции дифференцирования, то

легко доказать, что справедливо соответствие

UDHt

f (t)dt ↔

F(ω)

i2πω

Задача 4. Доказать, что

f (t − τ)

↔ e−i2πωτ F(ω), τ – число.

∞

введем

замену

∞

u = t − τ

f (t − τ) ↔ ò f (t − τ)e−i2πωt dt =

ò f (u)e−i2πω(u+τ) du =

t = u + τ

−∞

dt = du

−∞

∞

−i2πωτ

−i2πωu

−i2πωτ

www

du =e

F(ω). ▲

= e

ò f (u)e

−∞

Заметим, что | e−i2πω |=1. Поэтому операция запаздывания временного аргумента никак не отразится на модуле спектральной функции F(ω) .

44	www.studhelp.info

Задача 5. Обосновать формулу Рэлея

(u(t), v(t)) = (U (ω),V (ω)) (4.3)

– скалярное произведение сигналов u(t) и v(t) равно скалярному произведению их спектральных характеристик U (ω) и V (ω) .

Пусть u(t) и v(t) – комплексные сигналы, а U (ω) и V (ω) – соответственно их спектральные характеристики:

v(t) ↔ V (ω) =

∞

òv(t)e−i2πωt dt.

u(t) ↔ U (ω)

òu(t)e−i2πωt dt,

−∞

∞

−∞

Зная V (ω) , можно восстановить

−∞

v(t)

∞

v(t) = òV (t)ei2πωt dt.

Тогда для v * (t)

– комплексно сопряженной к

v(t)

функции – получаем

∞

UDH

v * (t)

òV * (t)ei2πωt dt .

−∞

Скалярное произведение функций u(t) и v(t) вычисляется так:

∞

используя

представление

(u, v) = òu(t)v * (t)dt =

формуле

−∞

v * (t)

по

предыдущей

∞

u(t)dt

V * (ω)e−i2πωt dω =

поменяем

двойном интеграле

порядок

интегрирования

−∞

∞

V * (ω)dω

u(t)e−i2πωt dt =

V * (ω)U (ω)dω = (U ,V ).

−∞

1442443

U (ω)

▲

Если формулу Рэлея (4.3) рассмотреть для случая v(t) = u(t) , то получим

(u,u) = (U ,U )

|| u(t) ||2 =|| U (ω) ||2 .

(4.4)

www

Формула (4.4) называется формулой Парсеваля-Планшеренеля. Оеа. говорит о

том, что нормы временной u(t) и

спектральной характеристик U (ω) сигнала

совпадают. Другими словами, если

f (t) ↔ F(ω) , то

f (t) ||=|| F(ω) ||,

45	www.studhelp.info

∞∞

||f (t) ||2 = ò f 2 (t)dt = ò F(w)F * (w)dw = || F(w) ||2 .

−∞ −∞

Здесь мы полагали функцию f (t) – временную характеристику сигнала –

вещественной.

Запишем в таблицу 1 сводку формул, теорем и правил соответствия временных f (t) и спектральных характеристик F(ω) .

Таблица 1. Свойства преобразования Фурье

f (t)

F(ω)

+∞

i2πωt

+∞

− 2πωt

f (t) =

F(w) e

F(w) =

f (t) e

ndt

−∞

−∞ .

Если

f * (t) = f (t),

то F(ω) = F * (−ω) | F(ω) |=| F(−ω) |

Четная симметрия:

f (−t) ≡ f (t)

F(−ω) = F(ω)

Нечетная симметрия:

f (−t) ≡ − f (t)

F(−ω) = −F(ω)

Линейность:

c1 f1(t) + c2 f2 (t)

c1F1(ω) + c2 F2 (ω)

Дуальность:

F(t)

f (−ω)

Изменение масштаба:

æ wö

f (kt)

Fç ÷

| k |

è k ø

Задержка во времени:

−i2πωτ

F(w)

f (t − τ)

UDH

Умножение на ei2πω0t :

F (ω − ω0 )

i2πω0t

f (t)

∞

Свертка:

ò f (u)g(t - u)du = f * g

F(ω)G(ω)

−∞

Произведение:

∞

f (t)g(t)

òF(w)G(w - u)du

www

−∞

Дифференцирование:

f ' (t)

i2πωF(ω)

Интегрирование:

F(ω)

i2pw

www.studhelp.info

ò f (t)dt

Формула Рэлея:

∞

ò f (t)g * (t)dt = ( f , g)

(F,G) = òF(w)G * (w)dw

−∞

Формула Парсеваля:

∞

ò| f (t) |2 dt

ò| F(w) |2 dt

−∞

4.2. Функция Дирака δ(t)

Физиком Дираком был рассмотрен

следующий пример. Материальная точка А

(шарик) до начального момента покоилась.

В момент t = 0 по ней ударили молоточком, после чего

она мгновенно перескочила в положение B ,

пройдя единичный путь А B , и

опять остановилась.

UDH0

Рассуждая как физик, Дирак предложил ввести функцию δ(t) :

ì0,

если

t ¹ 0,

d(t) = í

если

t = 0.

î¥,

При этом предполагается, что выполняются условия:

ì0,

если

t < 0,

d(t) = í

если

t ³ 0.

î1,

Теперь эту функцию называют дельта-функцией Дирака.

.ò

Обратимся теперь к удивительным свойствам этой функции:

www

∞ f (t)δ (t)dtS= ε f (t)δ (t)dt =

здесь

ε - скoль угодно

1º. −∞

−ε

малое

число > 0

= f (0) òδ (t)dt = f (0);

−ε

∞

2º. ò f (t)d(t - t0 )dt = f (t0 ).

−∞

Итак, дельта-функция обладает фильтрующим свойством: под знаком опре- деленного интеграла она выхватывает значение перемножаемой с ней функции при определенном значении аргумента t0 .

47	www.studhelp.info

Есть еще много удивительных свойств у дельта-функции (например, оказывается, что ее можно сколько угодно раз дифференцировать), но мы пока рассматривать их не будем.

Попробуем включить δ(t) -функцию в число сигналов и займемся ее спек-

тральным изображением. А попутно мир сигналов пополним еще кое-какими функциями.

4.3. Спектральная плотность постоянного сигнала

	n
Напомним, какие ограничения нужно наложить на функцию f (t)		для того,
чтобы ее можно было представить интегралом Фурье.	i	fo
Теорема 4.1. Если функция f (t)	.

1) кусочно-непрерывная на всей числовой оси R, имеет конечное число точек разрыва 1-го рода и конечное число точек экстремума на любом отрезке [−l,l]

(условие Дирихле);					L
					+∞
2) абсолютно интегрируема на всей числовой оси: ò\| Pf (t) \| dt = Q < +∞ ,
то для нее существует интеграл Фурье					−∞
то для нее существует интеграл Фурье
	+∞	UDH
			f (t − 0)	+ t(t + 0)
	ò F(ω)ei2πωt dω =		E			,
	−∞			2
который сходится при любом t к среднему значению левого и правого преде-
лов функции f (t) в точке t .
Заметим, что второе условие этой теоремы дает жесткое ограничение на
	T
класс функций f (t) , представимых интегралом Фурье. В дальнейшем мы будем
S
обсуждать, как можно изменить оператор Фурье, чтобы класс функций f (t)
мог быть значительно расширен.
.
Пусть f (t) = A – число. Этот сигнал,
wwwΦ(ω):					А	f (t) = A
вообще говоря, запрещен теоремой 4.1,					А	f (t) = A
+∞
так как условие 2) ò\| f (t) \| dt = Q < +∞				0			t
−∞				f (t) = A и осью t здесь беско-
здесь не выполнено. Площадь между графиком				f (t) = A и осью t здесь беско-

нечна. Но мы все-таки попробуем применить преобразование (4.1) чисто формально.

Пусть ϕ(t) – благопристойный сигнал, имеющий спектральную плотность

∞
Φ(ω) = òϕ(t)e−i2πωtdt .	(4.5)

−∞

Воспользуемся теперь формулой Рэлея:

www.studhelp.info

∞

( f , j) = (F(w), F(w)) Û ( f , j) = ò f (t)j * (t)dt = ò F(w)F * (w)dw = (F, F) .

−∞

(4.6)

В нашем случае левая часть формулы (4.6) в силу (4.5) дает

∞

(a)

−∞

A òj * (t)dt = AF(0) ,

а правая часть есть интеграл

−∞

∞

ò F(w)F * (w)dw = AF(0) .

Замечаем, что F(ω)

проявляет свойство 1º дельта-функции:

F(ω) = Aδ(ω).

Итак,

f (t) = A ↔ F(ω) = Aδ(ω) ,

а по принципу двойственности

Aδ(t) ↔ A.

Математики

UDH

договорились

δ(t) -функцию обозначать вектором единичной

длины, исходящим вертикально из начала координатE

Ý d(t)

Ý d(t - t0 )

t, тогда

t .

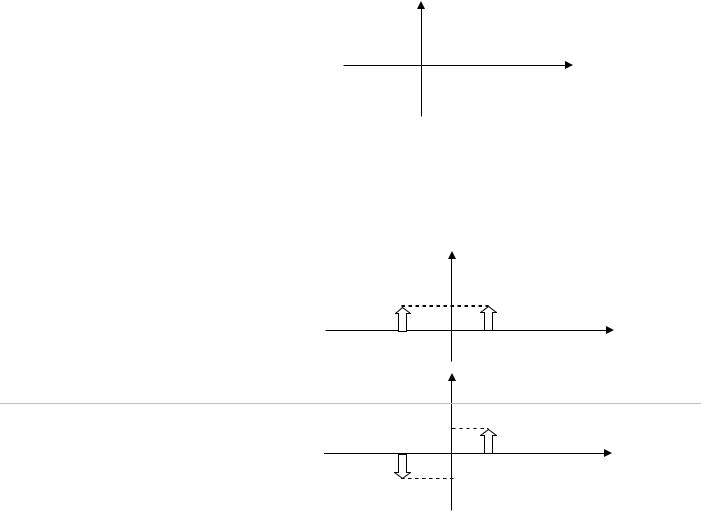
Поэтому образно в картинках наши последние выводы выглядят так:

Ad(w)

↔

Ad(t)

4.4. Спектральная плотность комплексного сигнала

www

Рассмотрим комплексное колебание

u(t) = ei2πωt

49	www.studhelp.info

с частотой ω в Герцах. Этот сигнал также не обладает свойством абсолютной интегрируемости на всей числовой прямой. Но оказывается, что для него спектральная плотность существует.

Задача 6. Доказать, что если

f (t) ↔ F(ω) ,

то

+∞

ei2πω0t f (t) « F(w - w0 ) .

D f (t) « F(w) = ò f (t) e−i2πωt dt;

−∞

+∞

ei2πω0t f (t) « ò

f (t) ei2πω0t × e−i2πωt dt = ò f (t) e−i2π(ω−ω0)t dt = F(w - w0 ).

−∞

▲

Возьмем теперь

f (t) =1. Тогда

f (t) ↔ δ (t) и, согласно итогу задачи 6,

ei2πω0t ×1 « d(w - w

)

Û ei2πω0t « δ (ωP- ω ) .

Заметим, что для вещественных сигналов f (t) модуль спектральной плотно-

сти есть четная функция от ω :

| F(−ω) |=| F(ω) |.

А теперь рассмотрим в качестве

сигнала ei2πω0t – комплексное

Ý d(w - w0 )

колебание, для которого

ω0

спектральная функция δ(ω − ω0 )

имеет

несимметрический модуль относительно вертикальной оси.

UDH

4.5. Спектральная плотность гармонических колебаний

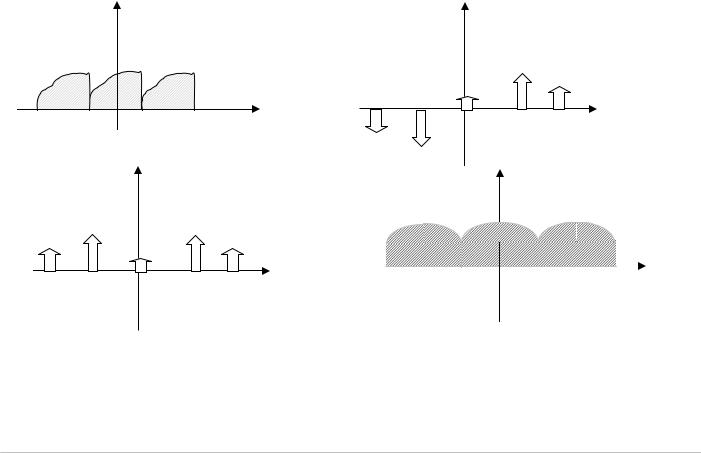
Вычислим спектральные характеристики простейших гармонических коле-

баний cos 2πω

t,sin 2πω

t . Для этого воспользуемся формулами Эйлера:

ei2πω0t + e−i2πω0t

δ(ω + ω )

δ(ω − ω )

1) cos 2πω0t =

d( - 0 ) + d(w + w0 )

;

-ω0

ω0

wwwei2πω0t - e−i2πω0t

δ(ω − ω0 )

sin 2πω0t =

-ω0

δ(ω − ω0 ) − δ(ω + ω0 )

δ(ω+ ω0 )

- 1

ω0

50	www.studhelp.info

4.6. Спектральная плотность произвольного периодического сигнала

Пусть дан периодический сигнал f (t) = f (t + 2l) . Представим его в виде ряда Фурье в комплексной форме и найдем его спектральную функцию:

∞	i	πnt
f (t) = åcn e		l	«

n=−∞

∞

F(ω) = å

n=−∞

æ		n ö
cnδ ç	ω -		÷ ,

è		2l ø

где

f (t)e−i

πn

an + ibn

− ibn

t dt , c =

−n

2l −l

Функция F(ω)

называется импульсной функцией.

Итак, преобразование Фурье для периодической функции времени представ-

ляет собой импульсную последовательность в частотной области, причем пло-

щади импульсов равны коэффициентам cn ряда Фурье.

В соответствии со

P свойством дуальности преобразование Фурье импульснойLпоследовательности

во временной области будет давать периодическую функцию частоты. Геометрически это выглядит так:

f (t)

F(ω)

↔

− l

UDH

f (t)

F(ω)

↔

- w

−

- 2

В аналитической форме рассмотренное выше соответствие имеет вид:

∞

n ö

∞

−i

πn

n ö

f (t) = å f [n]δ çt -

« F(ω) =

f [n]e

δ çt -

÷ ,

www

n=−∞

2w ø

n=−∞

2ω ø

πn

ω dω .

f [n] =

−òwF(ω)ei l

Тот факт, что преобразование Фурье периодической функции

f (t)

времени

t , заданной в виде периодической или импульсной последовательности, соответственно дает импульсную или периодическую последовательности в частотной области, фактически означает, что интегральные операторы прямого и об-

<<< < Предыдущая 1 2 3 45 / 125 6 7 8 9 10 11 12 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
24.02.20163.66 Mб9Lc2_2015_ПДС.pdf
#
24.02.2016824.37 Кб34metodichka_fizika_2_semestr.pdf
#
24.02.2016911.42 Кб8montag.pdf
#
24.02.201638.81 Кб36ozi_gavrilenkov481971_6.docx
#
24.02.20164.6 Mб12PADS_Eval_Guide.pdf
#
24.02.2016956.88 Кб11SMMiF_bsuir.pdf
#
24.02.20161.7 Mб10TM_Kontrol.pdf
#
24.02.20166.53 Mб143TM_Lectures.pdf
#
24.02.2016394.59 Кб10TM_Work_Plan.pdf
#
24.02.201647.62 Кб38Topics(вечерники).doc
#
24.02.2016540.29 Кб32tx_29 ТКС.docx