Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Институт информационных технологий БГУИР

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

SMMiF_bsuir

.pdf

Скачиваний:

Добавлен:

24.02.2016

Размер:

956.88 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 129 10 11 12 > Следующая >>>

81	www.studhelp.info

§ 7. Вариационное исчисление

Вариационное исчисление

зародилось в 1696 г., когда

Иоганн Бернулли поставил

задачу об отыскании кривой

«наибыстрейшего спуска» –

«брахистохроне». Эта задача

формулируется так:

Рис 7 1

из точки А в точку В (рис. 7.1) под действием силы тяжести безiначальной

скорости движется точка M(x,y(x)). Какой должна быть кривая АВ:

y = y * (x), x [a, b],

чтобы время спуска по ней было минимальным?

UDH

По закону сохранения энергии имеем

mv2

= mgy ,

откуда

v =

2gy

Тогда время пробега отрезка ds кривой АВ находится так:

Tds

dx2 + d 2 y(x)

1 + [ y'(x)]2

dx ,

2gy(x)

www

dt = v

а время спуска вдоль всей кривой АВ определится интегралом

1 + [ y'(x)]

dx .

2gy(x)

К концу 20 века вариационное исчисление, получившее свое обоснование в

работах Л. Эйлера, Ж. Л. Лагранжа, А.М. Лежандра и К. Вейерштрасса,

пере-

росло в математическую теорию оптимального управления, основателями которой явились Л.С. Понтрягин (Россия) и Р.Э. Беллман (США).

Простейшая задача вариационного исчисления

Дан функционал

J[ y(x)] = òF(x, y(x), y'(x))dx , a

www.studhelp.info

Задача 1.

(7.1)

сопоставляющий каждой кривой AB

y = y(x), x Î[a,b],

некоторое число J[ y(x)] .

Функция F(x, y, y' ) предполагается гладкой, т.е. ее частные производные до
второго порядка включительно по всем аргументам							fo
второго порядка включительно по всем аргументам				x, y, y' непрерывны в об-
						n
ласти					i
ласти					.
ìa £ x £ b		ü			P
ï		ï
D : í- ¥ < y < +¥		ý .
ï		ï
ï		ï	L
î- ¥ < y'< +¥þ

Среди функций y(x) ÎC 2 [a, b], удовлетворяющих краевым условиям
	E
y(a) = y A , y(b) = yB ,							(7.2)
UDH

требуется найти функцию y * (x) , на которой функционал (7.1) достигает экс-

тремума, т.е.

максимума

		T	J[ y * (x)] > J[ y(x)]
или
минимума			J[ y * (x)] < J[ y(x)],
			J[ y * (x)] < J[ y(x)],
где "y(x) ¹ y * (x)
где "y(x) ¹ y * (x)
Кривая AB : y = y * (x), x Î[a, b], в этом случае называется экстремалью.
	S
.
www

Для поиска решений этой задачи воспользуемся блестящей идеей Лагранжа. Примечательно, что к какой бы задаче Лагранж не приступал, он всегда нахо-

дил самое изящное (чисто во французском стиле) решение.

Пусть y * (x) – экстремаль для функционала (7.1), а dy(x) – зафиксированная

произвольная вариация, т.е. непрерывно-дифференцируемая функция, удовлетворяющая нулевым краевым условиям

dy(a) = dy(b) = 0.

(7.3)

Вариацию dy(x) будем добавлять к функции y * (x) , чтобы получить множест-

во функций y(x) , отличных от функции y * (x) .
Итак, рассмотрим множество функций
y(x) = y * (x) + t × dy(x),	(7.4)

83	www.studhelp.info

где параметр t изменяется так, что | t |<1.

Геометрически множество функций y(x) представить так:

A	y(x)
	y * (x)
	B

Рис. 7.2

Если в функционал (7.1) вставить

y(x)

в виде (7.4), то он превращается в

функцию j(t) :

J[ y(x)] = J[ y * (x) + t × dy(x)] = j(t),

которая достигает экстремума при t =0. Поэтому j'(0) = 0.

Найдем ϕ' (0) :

j'(t)

F(x, y * +t × dy, y * +t × dy')dx

t =0

¶t

t =0

(7.5)

b æ ¶F

¶F

dy +

UDH

dy')÷dx

= 0

¶y

¶y'

t=0

В выражении (7.5) преобразуем второе слагаемое:

интегрируем

по

частям

¶F

¶y' δy' dx = u =

¶y'

, dv = δy'(x)dx

¶y'

× δy(x)

¶F

= δy(x)

du =

÷dx, v

www

dx è

¶y' ø

¶F ö

æ ¶F ö

.d æ

(7.3)

÷δydx

a dx

÷δydx = -

a dx

÷δydx.

a dx è

¶y' ø

è ¶y' ø

¶y' ø

Итак, второе слагаемое в (7.5) имеет вид

b ¶F

b d

¶F ö

dy' dx = -

÷ × dydx ,

¶y'

ò dx è

¶y' ø

формулу (7.5) можно переписать так:

bæ

¶F

öö

(7.6)

òç

¶y

÷÷

dx è

¶y' øø

www.studhelp.info

Заметим, что (7.6) должно выполняться для любой функции δy(x) . Каков же

¶F

d æ

¶F ö

тогда множитель

ç ÷

? Ответ на этот вопрос дает лемма, доказанная

¶y

Эйлером:

dx è

¶y' ø

Лемма 7.1 (Эйлера). Если интеграл

òF(x) × dy(x)dx = 0

равен нулю для любой функции δy(x) , то функция Φ(x)

непременно должна

быть тождественно равна нулю:

Φ(x) ≡ 0 для x [a,b] .

Итак, согласно лемме Эйлера, экстремальная кривая y = y * (x) должна удов-

летворять уравнению Эйлера

¶F

d æ

¶F

= 0 .

(7.7)

¶y

¶y'

dx è

Таким образом, решение простейшей задачи вариационного исчисления све-

лось к решению уравнения (7.7) Эйлера при краевыхLусловиях (7.2). Заметим,

что Эйлер пришел к уравнению (7.7) первым, но путь его решения был более

сложным. Поэтому уравнение (7.7) называется уравнением Эйлера-Лагранжа.

А теперь обратимся к примерам.

пº1. Найти экстремаль функционала

J[ y(x)] = ò(y'2 -12xy)dx

при краевых условиях y(0) = 0, y(1) = 1.

D Приступая к решению нашейUDHзадачи, замечаем, что

¶F

d æ ¶F ö

F = y'

-12xy,

= -12x,

= 2y',

= 2y'' .

¶y

¶y'

www

¶y' ø

Поэтому уравнениеSЭйлера-Лагранжа (7.7) здесь выглядит так:

2y''−12x = 0 или y'' = 6x .

Интегрируя его, находим общее решение:

y(x) = x3 + c x + c

. Выделим те-

перь интересующее нас частное решение, потребовав, чтобы выполнялись

краевые условия:

ìy(0) = c2 = 0,

íy(1) =1 + c

+ c

=1.

Из последней системы находим: c1 = 0,c2 = 0. Следовательно,

y = x – иско-

мая экстремаль.

▲

пº2. Найти экстремаль функционала

						85	www.studhelp.info
						2
				J[ y(x)] = ò(2x - y 2 )dx
						1
при краевых условиях y(1) =1, y(2) = 3.
D Здесь F = 2x - y	2	,	∂F	= -2y,	∂F	= 0. Поэтому уравнение Эйлера-Лагранжа
D Здесь F = 2x - y		,	¶y	= -2y,	¶y'	= 0. Поэтому уравнение Эйлера-Лагранжа
			¶y		¶y'

имеет вид

− 2y = 0 или y = 0

и задает единственную экстремаль данного функционала, которая не удовлетворяет данным краевым условиям. Следовательно, у исходной задачи нет

гладкого решения.

▲

Отметим теперь некоторые частные случаи уравнения Эйлера-Лагранжа.

I случай. Пусть функция F = F(x, y)

не зависит от

y'. Тогдаiуравнение Эй-

лера-Лагранжа выглядит так:

∂F

= 0

или

¶y

ψ(x, y) =

0 .

(7.8)

Уравнение (7.8) определяет некоторую кривую, которая будет единственной

экстремалью для данного функционала (7.1). Для произвольных краевых усло-

вий (7.2) непрерывного решения, вообще говоря, нет.

II случай. Пусть F = F(y')

не зависит ни от х, ни от у. Тогда (7.7) имеет вид:

y'' = 0 .

Из общего решения

y = c1x + c2 находится единственное решение при крае-

вых условиях (7.2).

не зависит от y . Тогда уравнение (7.7)

III случай. Пусть F = F(x, y')

UDH

¶F

= 0

¶y'

∂F

= c1.

имеет промежуточный.

интеграл

¶y'

IV случай. Пусть F = F(y, y')

не зависит от x . Распишем подробнее уравне-

ние (7.7).

www

¶F

¶2 F

y'-

2 F

y'' = 0.

(7.9)

¶y

¶y'

¶y

¶y'2

F( y, y') - y' ∂F(y, y') = c .

(7.10)

Покажем, что уравнение (7.9) имеет первый интеграл

¶y' 1

Действительно, продифференцировав (7.10) по х, получим:

					86						www.studhelp.info
¶F		¶F		¶F	æ	¶2 F		¶2 F		ö
	y'+		y''-y''		- y'ç		y'+		2	y''÷	= 0
	y'+		y''-y''		- y'ç		y'+			y''÷	= 0
¶y		¶y'		¶y'	ç	¶y'¶y		¶y'		÷
¶y		¶y'		¶y'	è	¶y'¶y		¶y'		ø

или
æ	¶F		¶2 F		¶2 F		ö
ç		-		y'-		2	y''÷ y' = 0
ç		-		y'-			y''÷ y' = 0
ç	¶y		¶y'¶y		¶y'		÷
è	¶y		¶y'¶y		¶y'		ø

b=1

1 + y'2

Если последнее уравнение сократить на y', то получим в точности уравнение

(7.9).

▲

пº3. Обратимся теперь к задаче Бернулли о брахистохроне.

Дан функционал

T[ y(x)] =

2g a=0

и краевые условия y(a) = y A , y(b) = yB . Надо найти экстремаль.

D Приступая к обсуждению поиска решения этой задачи, замечаем, что по-

дынтегральная функция здесь не зависит от х, т.е. мы находимсяP

в условиях IV

случая. Поэтому должны воспользоваться формулой (7.10). Найдем

∂F

UDH

2 ,

y 1 + yE'

тогда

F - y' ¶F =

1 + y'2

y'2

= c .

¶y'

1 + y'

Упрощая левую часть последнего выражения, получаем

= c

1 + y'2

или

(7.11)

y(1+ y'2 ) = c .

Попробуем решить уравнение (7.11), введя замену

wwwТогда из уравнения (7.11)

y' = ctg t .

(7.12)

sin2 t

y =

= c

1+ y'2

1 + ctg2 t

или

y =

(1 - cos2t)

Мы нашли у как функцию от t . Теперь нам надо отыскать х как функцию от параметра t . Из (7.12) следует, что

www.studhelp.info

1 sin 2tdt

2 c1 sin t cos tdt

dx =

= 2 c1 sin

tdt

ctg t

cos t

или

sin t

dx = c1(1- cos2t)dt .

Отсюда, интегрируя по t , будем иметь

sin 2t ö

x = c1

çt

+ c 2

или

x =

(2t - sin 2t)+ c2 .

Полагая теперь 2t = ϕ, получим

x =

(j - sin j)

+ c

(7.13)

ïy =

(1 - cos j).

Система (7.13) задает кривую, называемую циклоидой.

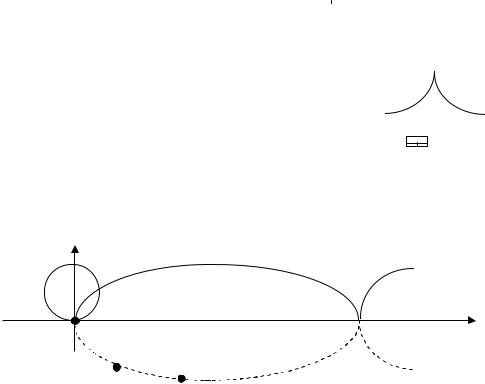
Заметим, что японцы, китайцы, вьетнамцы испокон веков строят крыши так, что их профиль есть циклоиды, с которых быстрее всего стекает вода (рис. 7.3).

	Несколько слов о том, что такое циклоида. Возьмем окружность радиуса R.
		T
Пусть она касается в начале координат оси Ox.
Будем теперь катить окружность как колесо
		S
вдоль оси Ox без скольженияUDHи наблюдать при
вдоль оси Ox без скольженияUDHи наблюдать при
этом за отмеченной точкой. Эта точка и
опишет циклоиду (рис. 7.4). Для решения
www		В
задачи о брахистохроне нам придется
циклоиду зеркально.отобразить относительно			Рис. 7.3
оси Ox и взять какой-то ее кусок AB .
		0		х
		А

Рис. 7.4

Мы не будем останавливаться на поисках значений постоянных c1 и c2 , при которых кривая (7.13) удовлетворяет краевым условиям y(a) = y A , y(b) = yB .▲

88 www.studhelp.info

пº4. (Задача о минимальной площади поверхности вращения).

Определить вид кривой

y = y * (x), x [a, b],

при вращении которой вокруг оси Ox образуется поверхность минимальной

площади.

D Приступая к решению

этой задачи, рассмотрим

вначале элементарную

площадь поверхности на

участке [x, x + dx] оси Ox.

Это усеченный конус.

ds(x) = 2πydl = 2πy

dx .

1+ y'2

Здесь dl – длина дуги кривой

AB над участком [x, x + dx].

Тогда вся площадь поверхности получается как интеграл

S[ y(x)] = 2pò y 1+ y'2 dx .

Краевые условия имеют вид

y(a) = y A , y(b) = yB .

Здесь подынтегральная функция F( y, y')

неEзависит от x . Поэтому восполь-

зуемся выражением

∂F

F - y'

= c .

¶y'

В нашем случае оно выглядит так:

+ y'

1 + y'2

= c

UDH1 + y'2

или, после упрощения,

y = c

1 + y'2 .

(7.14)

(7.14) – это.дифференциальноеS

уравнение первого порядка, неразрешенное

относительно производной. Чтобы разобраться, каковы здесь интегральные

кривые, введем замену y' = sh t . Тогда

1 + y'2 = ch2 t , y = c ch t, dx =

dy = y' dx

c1 sh tdt

= c dt, x = c t + c

sh t

Поэтому

www

ìx = c1t + c2

íy = c sht

– параметрические уравнения семейства интегральных кривых. Исключая

па-

раметр t , получаем семейство цепных линий

y = c1 sh x - c2 c1

y(a) = y A , y(b) = yB .

y = y(x), x [a, b], и краевые условия

J[ y(x)] = ò F(x, y, x')dz ,

89	www.studhelp.info

Цепная линия – это линия, по которой прогибается цепь, натянутая на точки А и В, по действием силы тяжести. Поверхность, получаемая вращением цепной линии вокруг оси Ox, называется катеноидом.

пº5. Дано: J[ y(x)] = ò( y2 − 2xy)dx , y(a) = y A , y(b) = yB . Найти экстремаль. a

Замечаем, что F = y 2 − 2xy не
зависит от y' и потому уравнение
зависит от y' и потому уравнение				С	fo
Эйлера-Лагранжа				площадь
∂F = 2y − 2x = 0				площадь
∂F = 2y − 2x = 0				Дидоны
∂y
имеет единственную экстремаль			A	in		B
y = x . Так что в общем случае				in

				О
непрерывного решения, удовлетворяющего				.
непрерывного решения, удовлетворяющего				P
произвольным краевым условиям,		море
вообще говоря, нет.	▲	море
вообще говоря, нет.	▲
пº6. (Изопериметрическая задача
пº6. (Изопериметрическая задача				L
Дидоны ).				L

E Существует легенда, согласноUDHкоторой Дидона – финикийская царица, – спа-

саясь от преследователей, на корабле приплыла в Северную Африку и попросила у местного царя кусок земли, который можно «окружить бычьей шкурой».

Царь, восхищенный молодостью и красотой Дидоны, немедленно дал согласие. Каково же было его удивление, когда Дидона у него на глазах разрезала шкуру вола на тесемки, связала их в длинную веревку, а потом, выбрав берег с боль-

T	2/3 своей веревки расстояние между точками А и
шим полуостровом, отмерила

В, нашла середину О отрезка AB и 1/ 3 веревки как радиусом описала полуок-

ружность с центром в точке О. Разложив свою веревку,Дидона отхватила у ме-

стного царя довольно большой кусок земли. Сначала она основала здесь крепость для себя., а потом на этом месте был построен город Карфаген (об этом

Рассмотрим общуюSзадачу. Дан функционал

можно прочитать в «Энеиде» римского поэта Публиа Вергилия Мероне). www

(7.15)

рассматриваемый на кривых AB :

(7.16)

Требуется найти экстремаль для функционала (7.15) такую, чтобы наряду с условиями (7.16) выполнялось дополнительное условие

G[y(x)] = òG(x, y(x), y'(x))dx = l = const ,

называемое изопериметрическим.

90	www.studhelp.info

Эта задача была поставлена Эйлером. Ж.Л. Лагранж дал для нее следующую изящную схему решения.

1 шаг. Составляем вспомогательную функцию Лагранжа:

L = F + λG ,

здесь λ – число, подлежащее определению.

2 шаг. Находим экстремали для уравнения Эйлера-Лагранжа, определяемого функцией L :

¶L -

¶L

÷ = 0 ,

¶y

¶y'

которые удовлетворяют краевым условиям (7.16).

Это и будет решением данной изопериметрической вариационной задачи.

Обратимся теперь к задаче Дидоны.

На математическом языке этуfoзадачу

можно сформулировать так: найти максимум площади S =

y(x)dx , ограни-

.ò 123

−a

ченной осью абсцисс и графиком функции

y = y(x) ,

x [−a,a] . Точкам А и В

оси Ox соответствуют координаты – а и а.

Функция

y(x) должна быть такой,

что:

1) ее график AB проходит через точки А и В, т.е. выполняются краевые усло-

вия y(−a) = y(a) = 0;

2) длина AB ограничена числом l = πa ≈ 3a , т.е. функционал

G[y(x)] =

1 + [ y'(x)]2 dx = pa .

1442443

Приступая к решению задачи Дидоны по схеме Лагранжа, составляем функ-

цию Лагранжа:

UDH

1 + y'

L = F + λG = y + λ

Замечаем, что L не зависитTот x , поэтому для нее вместо уравнения Эйлера-

Лагранжа выписываем первый интеграл

.Sæ

¶L ö

L - y'ç ÷

= c Û y - y'l

= c

1 + y'2

¶y'ø

www

y = c1 +

(7.17)

1 + y'2

де: y' = tg ϕ . Тогда

(7.17) – это дифференциальное уравнение первого порядка, не разрешенное относительно производной y'. Поэтому решение ищем в параметрическом ви-

y = c1 - λ cosϕ Þ y' = λ sin ϕ ddxϕ ; tgϕ = dydx Þ dx = tgdyϕ Þ .

Þ dx = λ cosϕdϕ Þ x = c2 + λ sin ϕ.

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 129 10 11 12 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
24.02.20163.66 Mб9Lc2_2015_ПДС.pdf
#
24.02.2016824.37 Кб34metodichka_fizika_2_semestr.pdf
#
24.02.2016911.42 Кб8montag.pdf
#
24.02.201638.81 Кб36ozi_gavrilenkov481971_6.docx
#
24.02.20164.6 Mб12PADS_Eval_Guide.pdf
#
24.02.2016956.88 Кб11SMMiF_bsuir.pdf
#
24.02.20161.7 Mб10TM_Kontrol.pdf
#
24.02.20166.53 Mб143TM_Lectures.pdf
#
24.02.2016394.59 Кб10TM_Work_Plan.pdf
#
24.02.201647.62 Кб38Topics(вечерники).doc
#
24.02.2016540.29 Кб32tx_29 ТКС.docx