Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Институт информационных технологий БГУИР

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

SMMiF_bsuir

.pdf

Скачиваний:

Добавлен:

24.02.2016

Размер:

956.88 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1210 11 12 > Следующая >>>

				91	www.studhelp.info
Но		ìy = c1	- lcosj	– это параметрические уравнения	окружности
Но		í	+ lsin j	– это параметрические уравнения	окружности
		îx = c2	+ lsin j
(x - c	2	)2 + (y - c )2 = l2		. При наших краевых условиях получим
	2		1

x2 + y2 = a2

– уравнение окружности Дидоны. ▲

Задачи для самостоятельного решения

Задача 1. Найти допустимые экстремали функционала

. .

J (x) = ò(12tx + x x+ (x)

)dt при условиях x(0) =1, x(1) = 4

Отв.: x = t

+ 2t

+ 1.

Задача 2. Найти экстремали функционала J (x) = et

1 + x

dt .

arccos(c e−t

Отв.: x = x(t) = c

Отв.: x = 0.

UDH

Задача 3. Среди кривых, соединяющих две точки A = (ch a, x1)

B = (ch b, x2 )

найти ту, которая при вращении вокруг оси t образует поверх-

ность наименьшей площади.

Отв.: x = ch t.

Задача 4. Найти экстремали функционалa:

. .

J (x) = ò(x + 2x x+ (x)2 )dt, x(0) = 0, x(1) = 0;

и B(1,0) и ми-

Задача 5. Найти кривую, которая проходит через точки A(0,1)

www

. 2

1 + x

нимизирует функционал.

J (x) = ò

dt.

§ 8. Приложения матриц к системам связи

Часто возникает необходимость использования матриц, разбитых (разложенных) на прямоугольные части или блоки. Например, m × n -матрицу

92 www.studhelp.info

æa

K a

A =

ça21

a22

K a2n

çKKKKKKKK

èam1

am2 K amn ø

можно разбить на 4 блока следующим образом:

æa

K a

ç 11

1k +1

ça

a22 K a2k

a2k +1

K a2n

çKKKKKKKKKK

KKKKKKKKK÷

A = ça

K a

lk +1

K a

= ç

çal +11 al + 22 K al +kn

al +1k +1 K al +1n ÷

çKKKKKKKKKK

KKKKKKKKK÷

èam1

am2 K amk

amk +1

K amn ø

где матрицы-блоки

PK a

æa

K a

æa

1n ÷

A =

K a

, A

L2k +1

çKKKKKKKKKK

çKKKKKKK

K a

ln ø

æa

l +11

l +

K a

l +kn

æa

l +1k +1

K a

A21 =

l +1n ÷

çKKKKKKKKKK

÷,

= çKKKKKKKKK÷

am2 K

èam1

amk ø

èamk +1

K amn ø

имеют соответственноTразмерностиUDHl × k,l × (n − k),(m − l) × k,(m − l) × (n − k) . Таким образом, с помощью горизонтальных и вертикальных линий m × n -

матрицу A можно рассечь на прямоугольные блоки.

Действия над блочными матрицами производятся по тем же формальным

правилам, что и в случае матриц с числовыми элементами. При этом, естест-
www						и B	= (B ) матрицы A и B и соответст-
венно, при сложенииSматриц A = (A )						и B	= (B ) матрицы A и B и соответст-
.					ij		ij
вующие блоки Aij и Bij				должны быть одинаковой размерности. При проведе-
нии операции умножения AB = C = (Cij ) матриц
		æ	A	A K A		ö	æ B11	K B1p	ö
	A =	ç	11	12	1l	÷	ç		÷
	A =	çKKKKKKKK ÷ и B = çKKKKKKKK÷
		ç	A	A	K A	÷	ç	K B	÷
		ç	A	A	K A	÷	ç B	K B	÷
		è	k1	k2	kl ø		è l1	lp	ø
необходимо, чтобы блоки Aik					и Bki были согласованными. Тогда
						æ	l	ö
						ç		÷
				AB = C = (Cij ) = ç			åaik bkj ÷.
						è k =1		ø

93	www.studhelp.info

Многочлен от матрицы. Пусть A – n × n-матрица с постоянными коэффициентами, а

a0λn + a1λn−1 + ... + an−1λ + an = Pn (λ)

– некоторый многочлен. Тогда

P (A) = a

An + a An−1 + ... + a

n−1

A + a

E ,

где E – единичная матрица, называется многочленом от матрицы A. Всякая

n × n-матрица A называется корнем многочлена Pn (λ) , если Pn (A) = 0, где 0 –

нулевая n × n-матрица.

Теорема 8.1 (Кели-Гамильтона). Всякая матрица является корнем своего

характеристического многочлена.

При построении обратнойfo

Пусть

λn + a λn−1 + ... + a

−1

λ + a

=| λE − A |.

матрицы A

−1

находится так называемая присоединенная или iсоюзная матрица

B , (i, j) -ый элемент

которой равен алгебраическому дополнению.

элемента

(a ji ) , причем матрица B удовлетворяет условию AB =| A | E . Это соотношение

верно для любой матрицы, а, следовательно, и для матрицыP(λE − A) . Присое-

диненной для матрицы (λE − A)

является матрица B(λ) , каждый элемент кото-

рой есть многочлен степени не выше n −1, так как он является минором ( n −1)- го порядка матрицы (λE − A) , т.е. имеет вид

где Bi

B(λ) = Bn−1λn−1 + Bn−2λn−2 + ... + B1λ + B0 ,

– матрицы n -го порядка с постоянными элементами. Тогда

(λE − A)B(λ) =| λE − A |,

или в подробной записи

(λE − A)(B

n−1

λn−1

+ B

n−2

λn−2 + ... + B λ + B ) = λn B

n−1

+ λn−1

n−2

− AB

n−1

) +

n−2

UDH

−2

+ λ

(Bn−3

− ABn−2 ) +

(−AB) = (λ

+ a1λ

+ a2λ

+ ... + an−1λ + an )E.

Приравнивая коэффициентыTпри одинаковых степенях λ, получим равенства

www

Bn−1 = E,

▲

0 = An + a1An−1

+ ... + an−1A + anE.

n−2

− AB

−1

= a E,

Bn−3 − ABn−2 = a2E,

KKKKKKKK

− AB = an E.

An , An−1,...,E ,

Умножая эти равенства последовательно на

и складывая, бу-

дем иметь

Передача дискретной информации. Сообщение

– это последовательность

дискретных

символов

(s1,s2,...,sr ) , выбираемых

из конечного

алфавита

(s1, s2 ,...,sk )

с вероятностями p1, p2,..., pk , p1 + p2 + ... + pk = 1. Так что источ-

94 www.studhelp.info

ник информации уподобляется случайной величине S , принимающей значения s j с вероятностями p j , j = 1,2,...,k.

При кодировании каждый символ источника заменяется последовательностью букв некоторого другого алфавита X = (x1, x2,...,xn ) , каждая из которых

предназначена для непосредственной передачи информации по линии связи. Очевидно, что каждой x j можно приписать некоторую вероятность π j .

Последовательность букв, соответствующая некоторому символу источника, называется кодовым словом. При декодировании осуществляется обратная операция с целью восстановления информации.

Для правильной передачи информации необходимо, чтобы значения физиче-

того, что на выходе принята выборка (β1,β2 ,...,β j ,...,βr ), если на вход подава-

ского явления, соответствующие буквам алфавита, отличались достаточно хо-
			fo
рошо одно от другого, иначе увеличивается риск получить искаженное сообще-
			n
ние. Колебание сигнала вокруг его среднего значения вызываетсяi«шумом», ко-
торый можно охарактеризовать вероятностью смещения двух.разных букв ал-
фавита.		,...,αi ,...,αr ) , а на вы-
Пусть на вход линии подается r -выборка A = (α1,α2
ходе принимается r -выборка B = (β1,β2		P
	,...,β j ,...,βr ) выходного алфавита. Ли-
	L
ния характеризуется множеством вероятностей перехода, т.е. вероятностей то-
го, что поданная на вход r -выборка (α1	,α2 ,...,αi ,...,αr ) принимается на выхо-
	E
де как r -выборка (β1,β2 ,...,β j ,...,βr ). Это условная вероятность
p(β1,β2 ,...,β j ,...,βr \| α1,α2 ,...,αi ,...,αr )
UDH

лась выборка (α1,α2	,...,αi ,...,αr ) .	i
	Ti	i

В этом случае говорят о линии передачи с памятью, в противном случае речь идет о линии передач без памяти.

В общем случае линия характеризуется случайной величиной X на входе,

принимающей значение x ,i =1,2,...,n. с вероятностями p , случайной величи-

ной Y на выходе, принимающей значения y j

с вероятностями π j , j = 1,2,...,n,

и матрицей перехода.SП, составленной из условных вероятностей

pij = p(Y = y j | X = xi ) .

Отсюда по формуле полной вероятности находим, что

æ p

K p

ç 11

(p , p

,...,p

) = ( p , p

,..., p

)ç p21

p22

K p2m ÷ .

(8.1)

www

çKKKKKKKK

è pn1

pn2 K pnm ø

Тогда по формуле Байеса можно вычислить условную вероятность

www.studhelp.info

pij = p(X = xi |Y = y j ) =

pij

(8.2)

å pi pij

i=1

пº1. Рассмотрим двоичную симметрическую линию, описываемую соотно-

шением

X {x1 = 0, x2 =1},

Y {y1 = 0, y2 =1},

т.е. на вход X и выход Y посылаются два значения 0 и 1 с вероятностями пе-

рехода

p00 = p(Y = 0 | X = 0) = p,

p01 = p(Y = 1| X = 0) = 1- p,

p10 = p(Y = 0 | X = 1) = 1- p,

p11

= p(Y = 1| X = 1) = p.

Матрица перехода П имеет вид

æ p

1- pö

(8.3)

П = ç

÷ .

è1- p

pø

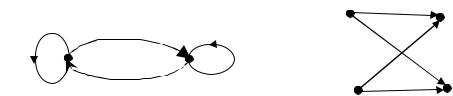
Граф перехода изображен на рис 8.1а, а сама линия перехода – на рис 8.1б.

а)

б)

1-p

1-p 1-p

Рис. 8.1

Основной проблемой при передаче информации является ограничение дейст-

вия шума на линии. Очевидно, что влияние шума будет тем меньше, чем боль-

наблюдая r -выборку на выходеUDH, можно было бы принять ее или отвергнуть в зависимости от того, подвергалось ли сообщение изменению в процессе пере-

ше вероятности πij , которые вычисляются по формуле (8.2). Практически задача водится к тому, чтобы определить правило принятия решения, по которому,

дачи. Другими словами, надо найти правило, которое позволяло бы обнаружи-
			T
вать ошибки и дало бы возможность их исправлять. Вероятность p , характери-
зующая шум на линии, обозначается p(l) .
		S
.
	пº2. Пусть линия передачи определяется случайной величиной X на входе,
принимающей значения x1, x2, x3, x4 с вероятностями
			p(X = x1) = 0.1,			p(X = x2 ) = 0.2,
			p(X = x3 ) = 0.3,			p(X = x4 ) = 0.4.
	Пусть число значений y j			случайной величины Y на выходе равно трем, а
матрица П имеет вид
	www
				æ	0.50	0	0.50	ö
				ç	0.20	0.40	0.40	÷
				ç	0.20	0.40	0.40	÷
				П = ç	0.50	0.25	0.25	÷.
				ç	0.50	0.25	0.25	÷
				ç	0	0.50	0.50	÷
				è	0	0.50	0.50	ø

														96				www.studhelp.info
Вычислим вероятности π j										= p(Y = y j ), j =1,2,3,						по формуле (8.1):
													æ	0.50	0	0.50	ö
				æ	1		2		3			4	ç	0.20	0.40	0.40	÷
				æ	1		2		3			4	öç	0.20	0.40	0.40	÷	= (0.24;0.355;0.405),
(p , p	2	, p	3	) = ç		,		,			,		÷	0.50	0.25	0.25	÷
(p , p		, p		) = ç	10	,	10	,	10		,	10	÷
1				è	10		10		10			10	øç
													ç				÷
													ç	0	0.50	0.50	÷
													è	0	0.50	0.50	ø

т.е π1 = p( y = y1) = 0.24, π2 = p(y = y2) = 0.355, π3 = p(y = y3) = 0.455 .
Расстояние Хэмминга. Пусть получен код, в котором каждая	fo
	r -выборка за-

кодирована словом, состоящим из n символов. Предполагается, что символы

взяты из конечного множества, обладающего тем свойством, что символы мож-
но складывать и перемножать (по определенным законам).					i
i	j				.
Расстояние Хэмминга – это расстояние между двумя кодовыми словами. Оно
определяется как число мест, в которых символы этих слов не совпадаютn.
пº3. Пусть кодовые слова c и c	имеют вид (в двоичном коде {0,1}):
ci = (1,0,1,1,0,0,0,1,1,0,1),			L
		c j = (0,1,1,0,1,1,0,1,0,0,0) .
		E		P
Для них расстояние Хэмминга d(ci , c j ) = 7 .

Расстояние Хэмминга тесно связано с вероятностью ошибки при передаче

информации или сообщения. Действительно, пусть передано слово αi , которое
	UDH	d(αi ,β j ) = δ.
принято как β j , причем расстояние Хэмминга			Тогда условная
вероятность	p(αi \| β j ) = pδ (1 − p)n−δ .
			(8.4)

В самом деле, при передаче символа из двоичной симметрической линии (матрица перехода (8.3)) вероятность ошибки равна p , а по линии передано

n − δ символов правильно, а δ символов неверно. В силу независимости передачи символов вероятность ошибки при передаче сообщения выражается фор-

мулой (8.4).	.				i
Так как на практикеTвероятность		αk			αo
p всегда меньше 0 5 (если линия		αk			αo
www				α
делает больше 50%Sошибок, то				α
вряд ли такой линией стоит
пользоваться), то p(αi \|β j )					δi
увеличивается, когда δ уменьшается.			δk		δo
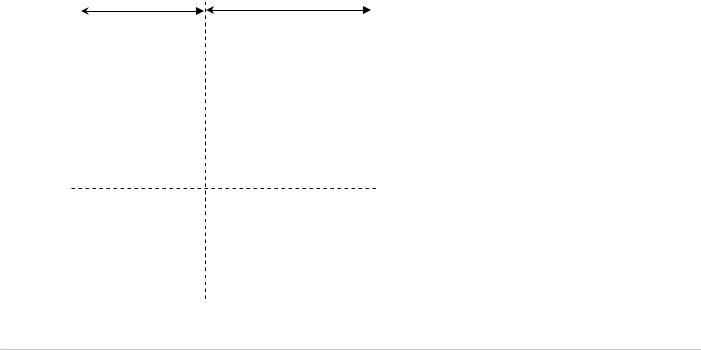
Отсюда получается следующее правило:					β j
при получении на выходе кодового слова					β j
β j следует в качестве кодового слова на					Рис.8.2
входе брать слово с наименьшим расстоянием от β j			(рис. 8.2). Если δi < δo и
δi < δk , то сигнал подается по линии δi .

Легко проверить, что расстояние Хэмминга удовлетворяет всем обычным аксиомам функции расстояния:

www.studhelp.info

а) d(ci , c j ) ³ 0, причем равенство d(ci ,c j ) = 0

выполняется тогда и только

тогда, когда ci = c j ;

б) d(ci , c j ) = d(c j , ci );

в) неравенство треугольника d(ci ,c j ) £ d(ci ,ck ) + d(ck ,c j ) .

Двоичные линейные коды. Пусть ei

= (0,0,...,0,1,0,...,0) – n -вектор, все ко-

ординаты которого, кроме i -ой, равны нулю, а i -ая координата равна единице.

Как известно, эти векторы в совокупности линейно независимы и образуют ба-

зис линейного пространства R n . В композиции они составляют единичную

матрицу E :

æ1

K 0

E = çKKKKKKKK÷ .

Пусть вектор ( n -выборка)

1ø

ai = (a ,a

,...,a

) ,

где ai – элементы поля алфавита. Матрицей E он преобразуется в вектор

aiE = (a ,a

,...,a

) ,

т.е. преобразование с матрицей E не искажает входной сигнал. Если взять дру-

гие n линейно независимых векторов и записать их как строки, то при умноже-

нии вектора а на матрицу М с этими строками,

в общем случае aM ¹ a . По-

скольку строки матрицы М независимы, то матрица М невырожденная и, следо-

вательно, умножением на соответствующий

a j (aiM = a j Û ai = a jM −1) по-

UDH

лучаются все векторы из R n .

Точно так же можно определить матрицу М, строки которой представляют

собой m линейно независимых векторов (их ранг равен m ). С помощью этой

, элементами которого

матрицы можно.получить все векторы пространства R

являются все выборки поля векторов ai

= (a , a

,...,a

) .

Напомним, что элементарные операции над матрицами (перестановка строк

местами; умножение любой строки матрицы на ненулевой элемент; прибавле-

ние к строке матрицы другой строки, умноженной на элемент поля чисел) не

меняют ранга матрицы и с их помощью любую m × n -матрицу ранга m можно

привести к следующему каноническому виду:

www

æ1

K 0

a1m+1

K a1n

ç0

2m+1

= (EM A).

B = ç

çKKKKKKKKKKKK

1 amm+1

è0 0 K

amn ø

(8.5)

простран-

ответствующими координатами выборки а, т.е. ai = bi ,i =1,2,...,m,

При таком преобразовании первые m координат вектора

98	www.studhelp.info

При этом строки матрицы В, как векторы, определяют то же линейное пространство, что и векторы-строки исходной матрицы. Матрица В преобразует m -выборку a = (a1, a2 ,..., am ) в n -выборку b = (b1, b2 ,...,bn ) :

b = (b1,b2,...,bn ) = aB .

b совпадают с со-

а последние k = n − m координат являются их линейными комбинациямиfo. Таким образом, мы приходим к кодам, которые называются систематическими. При переходе кодового слова первые m мест называются информационнымиn , а последние k = n − m – проверочными, так как эти линейные комбинацииi позволяют обнаружить и даже исправить ошибки при передаче информационных

символов. Такой код обозначается (n,m). Если использовать линейные про-
	P
странства над полем из двух элементов, то, как известно из.комбинаторики, с
его помощью можно передать 2m сообщений.
Линейный код общего вида состоит из всех векторов некоторого подпро-
E
странства линейного n -мерного пространства.
Двойственный код. Исходя из кода (n,m), можноLнепосредственно образо-
UDH

вать так называемый двойственный код (m,n). Действительно, если R m -

подпространство, порожденное строками матрицы В, то его базис можно следующим образом дополнить до базиса всего пространства R n :

æ1

K 0

0 0 1 K 0

aij

B → ç

çKKKKKK

i =1,2,..., m; j =1,2,..., j.

K 1

0 ÷

H → ç

b ji = -aij

KKKKKK

wwwn

Последние k = n − r векторов образуют базис подпространства R k

ства R . Пусть A = (aij ) – m × k -матрица с элементами aij . Тогда в соответст-

вии с записью (8.5):

B = (Em×m MA), H = (- AT MEk×k ).

При этом имеет место следующее матричное соотношение

100

z = HwT

Обнаружение ошибок. Для вектора v из подпространства R m , порожденного строками матрицы В, имеет место равенство (8.8). Если теперь на выходе получается некоторый n -мерный вектор w , для которого выполнено соотноше-

www.studhelp.info

BH T = (HBT )T = 0 .

(8.6)

В самом деле, записывая сомножители с помощью блоков, получаем

æ- A

(Em×m M A)ççKK

÷÷ = (- A)- (A) = 0.

è Ek×k

Пространство, порожденное векторами-строками матрицы В, называется ну-

левым пространством матрицы H , и наоборот. Если v – n -мерный вектор,

полученный из m -выборки а с помощью матрицы В, т.е.

то в силу равенства (8.6) имеем

v = aB ,

= aBH

= 0 .

(8.7)`

Таким образом, H

переводит в нулевой вектор любой векторiv

из R

Транспонируя равенство (8.7):

HvT = 0T ,

(8.8)

где vT и 0T – k -векторы-столбцы. Уравнение (8.8) представляетP

собой систему

k линейных однородных уравнений

с неизвестными v1,v2,...,vk . Векторы

v =(v1,v2,...,vk ), координаты которых являются символами кодовых слов на

контрольных листах, – это решение системы (8.8). Ввиду этого матрица H на-

зывается проверочной матрицей.

UDH

ние		T			HwT ¹ 0 ,
		T
	S
то w не принадлежит R			m	и, следовательно, обнаружена ошибка. Заметим, что,
то w не принадлежит R				и, следовательно, обнаружена ошибка. Заметим, что,
	.

очевидно, при выполнении равенства(8.8) можно лишь утверждать, что при передаче по линии не произошло ошибки какого-то определенного типа, но нет

wwwгарантии, что отсутствуют ошибки других типов. В самом деле, вектор

имеет k координат и поэтому не дает возможности выявить больше, чем pk -1 типов ошибок, где p – число элементов поля. Поэтому необходимо с самого начала установить, какие ошибки желательно обнаруживать. В частности, в двухкодовом поле {0,1} можно выявить не более 2k -1 типов ошибок.

§ 9. Эйлеровы функции Γ(x) и B(x, y)

Гамма функция Γ(x) . Интегральное представление гамма-функции Γ(x) определяется равенством

101

100	www.studhelp.info

∞

G(x) = òt x−1e−t dt, x > 0.

(9.1)

Этот интеграл сходится при x > 0, так как при t → ∞ он сходится из-за нали-

чия множителя e−t ,

а при t → 0 выполняется

e−ttx−1 ~ t x−1. Отсюда следует,

что интеграл (9.1) существует при x −1 > −1, т.е. при x > 0.

Производная Г-функции (9.1)

∞

G'(x) = òt x−1e−t ln t dt, x > 0.

Аналогично получаем

∞

x−1 −t

G''(x) =

> 0.

(ln t)

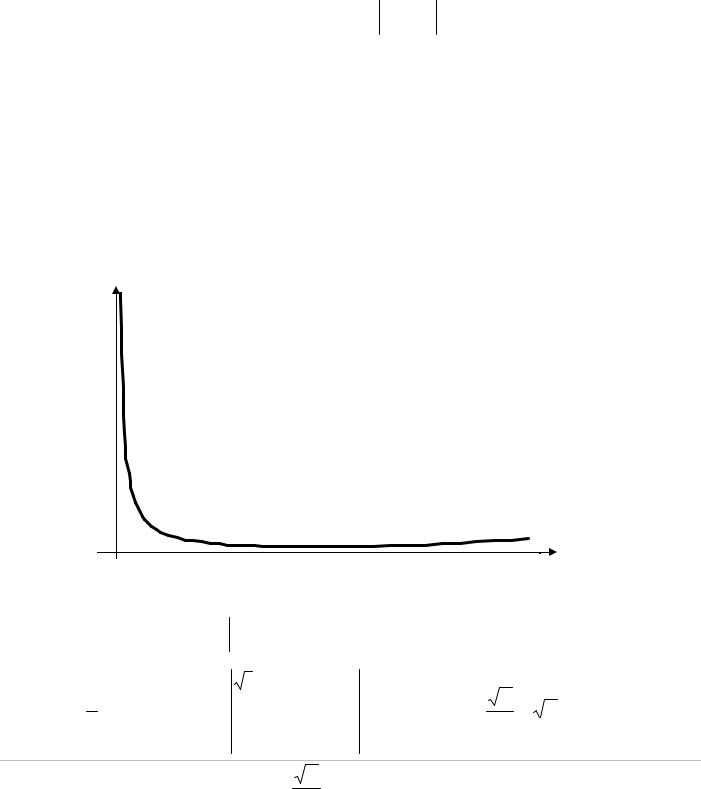
Отсюда следует, что гамма-функция является выпуклой функцией, имеющей

единственный положительной минимум (рис. 9.1).

Г(х)

UDH

Рис. 9.1

∞ =1;

пº1. а) G(1) = òe−t dt = - e

−t

1 ö

t = s, dt = 2s ds

∞

= òe−tt−1/ 2dt = t = 0 Þ s = 0

ò2e−s

ds =

2 ×

π ,

б) Gç

2 ø

t = ¥ Þ s = ¥

www

∞

ds =

π .

так как интеграл Пуассона

òe

−s

Формула приведения. Интегрируя по частям в равенстве (9.1), получаем

102

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1210 11 12 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
24.02.20163.66 Mб9Lc2_2015_ПДС.pdf
#
24.02.2016824.37 Кб34metodichka_fizika_2_semestr.pdf
#
24.02.2016911.42 Кб8montag.pdf
#
24.02.201638.81 Кб36ozi_gavrilenkov481971_6.docx
#
24.02.20164.6 Mб12PADS_Eval_Guide.pdf
#
24.02.2016956.88 Кб11SMMiF_bsuir.pdf
#
24.02.20161.7 Mб10TM_Kontrol.pdf
#
24.02.20166.53 Mб142TM_Lectures.pdf
#
24.02.2016394.59 Кб9TM_Work_Plan.pdf
#
24.02.201647.62 Кб38Topics(вечерники).doc
#
24.02.2016540.29 Кб32tx_29 ТКС.docx