
SMMiF_bsuir
.pdf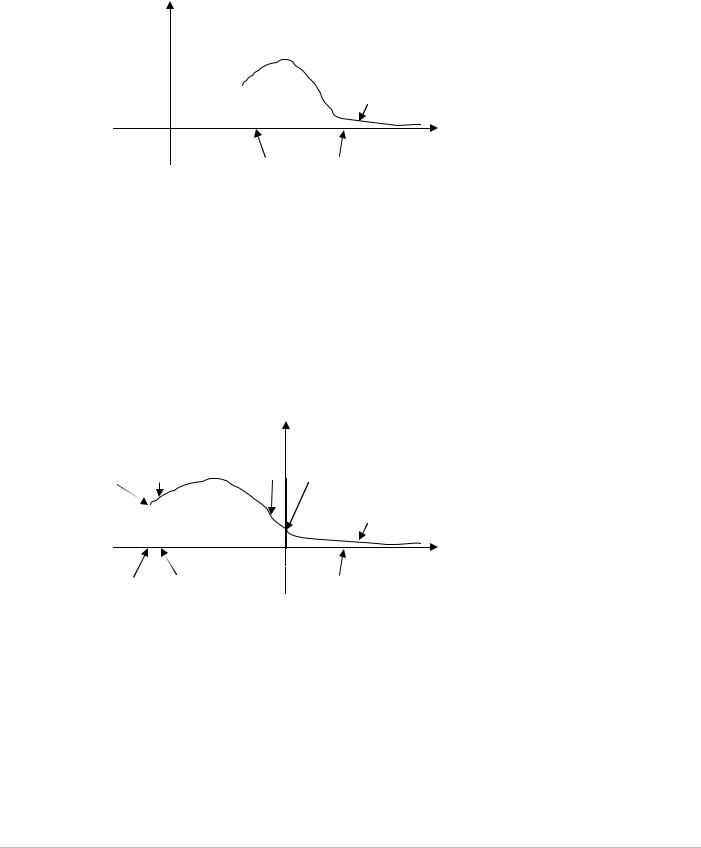
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
71 |
|
|
|
|
|
|
|
|
|
|
|
|
|
www.studhelp.info |
|||
|
|
f(n-k) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
f(1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
f(0) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f(n) |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
fo |
||||||
Тогда f (n - k) « f (0) + |
|
f (1) |
+ ... + f (n) + ... = F(z) . ▲ |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k+1 |
|
|
|
|
|
k+n |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 6.4 |
|
|
|
|
n |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
||
|
|
|
|
|
|
|
z k |
z k+1 |
|
|
|
|
|
|
z n+k |
z k |
. |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
Теорема 6.3 (опережения аргумента). Если f (n) ↔ F(z) , то |
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
é |
|
æ |
|
|
|
|
|
f (1) |
|
|
|
|
|
|
|
f (k -1) |
L |
|
|
|
|
||||||||||||||||
f (n + k) « zk |
ê |
F(z) - ç f (0) + |
|
|
|
+ ... + |
|
|
|
|
|
|
÷ |
. |
|
|
|
|
|
||||||||||||||||||||
|
|
|
ç |
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
zk −1 |
÷ú |
|
|
|
|
|
|
||||||||||||||
|
|
ë |
|
è |
|
|
|
|
|
|
|
|
|
|
|
|
|
øû |
|
|
|
|
|
|
|||||||||||||||
D Действительно, график функции |
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
||||||||||||||||||||||||
|
f (n + k) – это график функции f (n) , |
||||||||||||||||||||||||||||||||||||||
сдвинутый на k шагов влево по оси t |
как твердое тело (см. рис. 6.5). |
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
UDH |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f(n+k) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
f(0) |
|
f(1) |
|
|
|
|
f(k-1) f(k) |
|
|
f(n-k) |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
T |
|
|
-1 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
||||||||
|
|
-k |
|
|
|
–k+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 6.5
Все, что расположено левее оси ординат, зануляется. Мы должны использо- |
|||||||||||
вать только ту часть решетки, которая имеется справа от оси ординат, т.е. учи- |
|||||||||||
www |
|
|
|
|
|
|
|
|
|
|
|
тывать только.значенияSf (k),..., f (n − k),.... |
|
|
|
|
|
|
|||||
Итак, имеем: |
|
|
|
f (k + 1) |
|
f (k + n) |
|
|
|||
|
f (n + k) « f (k) + |
|
+ |
+ ... = |
|||||||
|
|
|
|
||||||||
|
|
|
|
|
z |
|
|
|
z n |
|
|
|
k é |
æ |
|
|
f (1) |
|
|
|
f (k - 1) öù |
||
|
|
ç |
+ |
|
+ ... + |
|
|
÷ |
|||
|
|
|
|
|
|||||||
|
= z êF(z) - ç f (0) |
z |
z k−1 |
÷ú. |
|||||||
|
ë |
è |
|
|
|
|
|
øû |
|||
|
|
|
|
|
|
f (n) |
|
▲ |
|
Теорема 6.4 (подобия). Если |
f (n) ↔ F(z) , то |
|
« F(az) . |
||||||
|
an |
||||||||
|
|
|
|
|
|
|
|||
D Если f (n) « F(z) º f (0) + |
f (1) |
+ |
f (2) |
+ ... + |
f (n) |
+ ..., то |
|||
z |
z 2 |
z n |
|||||||
|
|
|
|
|
|||||
73

|
|
|
|
|
|
72 |
|
|
|
|
|
|
|
|
www.studhelp.info |
|
f (n) |
↔ F(z) ≡ f (0) + |
f (1) |
+ |
|
f (2) |
+ ... + |
f (n) |
|
+ ... = F(az) . |
▲ |
||||
|
|
|
(az)2 |
|
|||||||||||
|
an |
az |
|
|
|
(az)n |
|
||||||||
Теорема 6.5 (о дифференцировании Z -изображения). Если |
f (n) ↔ F(z) , |
||||||||||||||
то nf (n) ↔ −zF'(z) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
По определению F(z) ≡ f (0) + |
|
f (1) |
+ |
f (2) |
+ ... + |
f (n) |
+ .... Продифферен- |
||||||||
|
|
z 2 |
|
||||||||||||
|
|
|
|
|
|
z |
|
|
|
|
z n |
|
|||
цируем по z это тождество (это можно сделать, так как ряд Лорана равномерно
сходится к F(z) ): F'(z) ≡ − |
f (1) |
− 2 |
f (2) |
− ... − n |
f (n) |
+ .... А теперь умножим на |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z2 |
|
|
|
z3 |
|
|
|
|
|
zn+1 |
|
|
|
|
|
|
|
n |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (1) |
|
|
f (2) |
i |
f ( ) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
fo+ .... |
|||||
(- z ) обе части последнего равенства: |
− zF'(z) ≡ |
|
z |
+ 2 |
z |
|
2 |
+ |
+ |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
||||||
Всмотревшись в коэффициенты последнего ряда Лорана, замечаем, что спра- |
|||||||||||||||||||||||||||||||||||||||||||||||
ведливо соответствие nf (n) ↔ −zF'(z) . |
|
▲ |
|
|
|
|
L |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
Теорема 6.6 (о свертке). Если |
f (n) ↔ F(z),ϕ(n) ↔ Φ(z) , то |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
f (n) * ϕ(n) = |
å f (k)ϕ(n − k) |
↔ F(z)Φ(z). |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Обозначим через g(n) |
UDH |
|
|
|
|
|
|
|
|
|
|
|
|
f (n) и ϕ(n) : |
||||||||||||||||||||||||||||||||
|
свертку двух решетчатых функций |
||||||||||||||||||||||||||||||||||||||||||||||
g(n) = å f (k)ϕ(n − k) , а через G(z) – |
|
Z -изображение для g(n). По определе- |
|||||||||||||||||||||||||||||||||||||||||||||
|
k =0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
нию |
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− k) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
∞ |
g(n) |
∞ |
å f (k)ϕ(n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
G(z) = å |
|
|
= å |
k=0 |
|
|
|
|
|
|
|
|
|
|
|
|
= |
изменим |
|
порядок суммирования |
= |
|||||||||||||||||||||||||
z |
n |
|
|
|
|
|
|
z |
n |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
n=0 |
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
n=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
∞ |
|
|
∞ |
ϕ(n − k)Tвведем |
замену |
|
∞ |
|
|
|
|
∞ ϕ(m) |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
. |
|
|
= m = n − k |
|
|
|
|
|
|
|
= å f (k) å |
|
|
= |
|
|
|
|
|||||||||||||||||||||||||
|
= å f (k) å |
|
z n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
k=0 |
n=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k=0 |
|
|
m=0z m+k |
|
|
|
|
|
|
|
|
|||||||||||
www |
|
|
|
|
|
|
n = m + k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
∞ |
f (k) |
∞ |
ϕ(m) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
= å |
|
|
å |
|
= F(z)Φ(z). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
z k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
k=0 |
m=0 z m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1424314243 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
F (z) |
|
Φ(z) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
▲ |
|
Итак, необходимые нам в дальнейшем теоремы мы обсудили. Теперь соста- |
||||||||||||||||||||||||||||||||||||||||||||||
вим для дальнейшего |
|
использования |
|
на |
практике таблицу |
соответствия |
|||||||||||||||||||||||||||||||||||||||||
f (n) ↔ F(z) . |
|
|
∞ |
|
a |
n |
|
|
|
|
a |
|
a |
2 |
|
|
|
|
|
|
a |
n |
|
|
|
|
|
1 |
|
|
|
|
|
z |
|
|
|
||||||||||
|
|
f (n) = an |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
пº1. |
↔ å |
|
|
=1 + |
+ |
|
|
|
+ ... + |
|
|
+ ... = |
|
|
= |
|
|
. |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
n=0 zn |
|
|
|
|
|
z |
|
|
z2 |
|
|
|
|
|
zn |
|
|
|
1 − |
|
|
|
z |
− a |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
74

73 www.studhelp.info
|
пº2. f (n) = e jβn « |
|
|
|
|
z |
|
. Тогда для f (n) = e− jβn |
« |
z |
|
. |
|
|
|||||||||||||||||||||||||||||||||
z |
- e jβ |
z - e− jβ |
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
пº3. cosbn = |
e |
jβn |
+ e |
− jβn |
|
« |
|
1 |
|
é |
|
|
|
|
z |
|
|
|
+ |
|
z |
|
|
ù |
= |
|
z(z - cos bn) |
. |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
ê |
|
|
|
|
|
|
|
|
|
|
ú |
|
|||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
z - e− jβ |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ë z - e jβ |
|
|
û |
|
|
z 2 - 2z cosb + 1 |
|||||||||||||||||||||||||
|
пº4. sinbn = |
|
|
z sinβ |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
z2 - 2z cosb +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
fo |
|||||||||||||||||
|
пº6. f (n) = (-1)n « z + 1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
пº5. f (n) =1=1n « |
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
z -1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
|
|
|
z |
ö' |
|
|
|
|
|
z |
|
|
|
|
|
P |
|
|
|
|||||||||
|
пº7. j(n) = nf (n) = n ×1n « (-z)ç |
|
|
|
|
|
|
÷ = |
(z -1)2 |
|
. |
|
|
|
|
|
|
in |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è z -1ø |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|||||||||||||||
|
|
|
|
|
æ |
|
|
z |
|
|
|
|
ö' |
|
|
|
|
|
z(z +1) |
|
|
|
|
L |
|
|
|
|
|||||||||||||||||||
|
пº8. n2 = nj(n) « -zç |
|
|
|
|
|
|
÷ = |
. |
E |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
ç |
(z - |
1) |
2 |
÷ |
|
|
|
|
|
(z -1) |
3 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
è |
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (n) по ее Z - |
||||||||||||||||||
|
Рассмотрим теперь |
вопрос |
|
о |
|
|
|
восстановлении функции |
|||||||||||||||||||||||||||||||||||||||
изображению F(z) . |
|
|
|
|
|
|
|
|
|
UDH |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Задача 1. Дано F(z) . Найти f (n) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
D Приступая к обсуждению решения этой задачи, прежде всего вспомним, |
||||||||||||||||||||||||||||||||||||||||||||||
что |
|
|
|
|
|
|
|
|
|
|
|
|
|
f (1) |
|
|
|
f (2) |
|
|
|
|
|
f (n) |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
F(z) º f (0) + |
|
+ |
|
+ ... + |
|
+ ... . |
|
|
(6.5) |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
T |
|
|
|
z |
|
|
|
|
|
|
z 2 |
|
|
|
|
|
|
|
z n |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
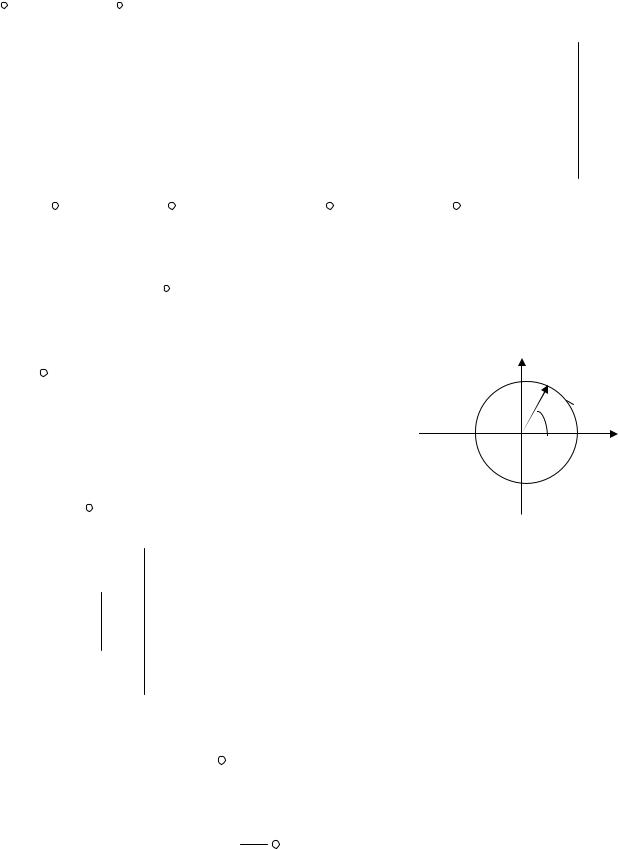
Ряд Лорана в тождестве (6.5) сходится абсолютно и равномерно в области D' |
||||||||||||||||||||||||||||||||||||||||||||||
(см. рис. 6.6). |
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Im z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 6.6 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
www |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
D' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
RRZ |
|
|
|
Re z |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
’ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
Возьмем в области D' |
окружность L радиуса R > R |
|
= es0 . |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
||
|
Умножим обе части тождества (6.5) |
|
на zn−1 и проинтегрируем по окружно- |
||||||||||||||||||||||||||||||||||||||||||||
сти L обе части полученного тождества
75
74 www.studhelp.info
|
|
|
|
|
n−1 |
|
|
|
|
|
|
|
æ |
|
|
|
|
|
|
|
n−1 |
|
|
|
|
|
f (1)z |
n−1 |
|
|
|
|
|
|
|
|
f (n)z |
n−1 |
|
ö |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
ò F(z)z |
|
|
= ò |
ç |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
dz |
ç f (0)z |
|
|
+ |
|
|
|
|
|
|
|
|
|
+ ... + |
|
|
|
|
|
|
|
|
|
|
|
+ ...÷dz |
= |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
z |
n |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
L |
|
|
|
|
|
|
|
|
|
|
|
L |
è |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
ряд f (0)z n−1 + |
f (1)z n−1 |
|
+ ... + |
f (n)z n−1 |
|
|
|
+ ... |
|
сходится |
|
|
равномерно, |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
z n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
= |
поэтому |
интеграл |
от |
|
|
|
суммы |
|
равен |
|
|
|
|
|
|
|
|
|
|
|
|
L z m− +1 |
|
|
|
|
= |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
от |
|
|
|
|
слагаемых |
L z |
|
|
|
|
|
|
|
|
|
fo |
||||||||||||||||||||||||||||
|
|
сумме |
|
|
интегралов |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
= f (0)ò z n−1dz + f (1)ò z n−2dz + K + f (n)ò |
dz |
|
|
|
|
|
|
|
f (m)ò |
|
|
|
dz |
n |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
+ K + |
|
|
|
|
|
|
+ K. (6.6) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Напомним, что в комплексном анализе мы доказывали, что |
i |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dz |
|
|
|
|
|
ì |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
0, |
если |
|
|
m ¹ n, |
|
|
|
|
|
|
|
. |
|
(6.7) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
í |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Lò z m−n+1 |
|
|
|
|
|
|
|
|
|
|
|
m = n. |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
î2πi, если |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
Покажем еще раз, как можно доказать формулу (6.7): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
dz |
|
|
|
z = Re |
it |
|
|
|
|
|
2π |
i Reit |
dt |
|
2π |
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
1) |
|
ò |
|
|
= |
|
|
|
|
= |
|
|
ò |
|
= |
ò |
|
idt = i2p. |
|
|
|
|
|
|
|
|
|
|
Im z |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
z |
|
|
dz = Rieit dt |
|
|
|
|
|
|
|
Reit |
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
L:|z|=R |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
t |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Re z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dz |
|
|
|
|
|
z = Reit |
|
|
|
|
|
|
|
|
2π i Reit |
|
|
dt |
|
|
i 2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
2) k ¹ 1: |
|
|
ò |
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
it |
|
|
= |
ò |
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
òe−i(k−1)t dt = |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
k |
|
|
dz = Rie |
|
dt |
|
(Re |
it |
) |
k |
R |
k |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
L:|z|=R z |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в силу |
|
|
периодичности |
функции |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−i(k−1) tUDH |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
−i(k−1)t |
|
2π |
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
результаты |
|
|
подстановки |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
ie |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
= - |
Ri(k -1) |
|
|
|
|
|
= верхнего |
|
|
|
и |
|
нижнего |
|
|
|
|
пределов |
|
|
|
|
= 0. |
|
|
|
(6.8) |
||||||||||||||||||||||||||||||||||||||
www |
|
|
|
|
|
|
|
|
|
|
|
|
f (n) = |
|
1 |
|
ò F(z)z n−1dz . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
совпадают; |
|
поэтому |
|
при |
вычитании |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
получаем |
|
|
|
|
ноль |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
Таким образом, в правой части тождества (6.6) остается только одно слагае- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
мое, отличное от нуля, и это тождество можно переписать так: |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
òF(z)zn−1dz = f (n)2pi . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Откуда и определяется |
f (n) : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2pi L
К интегралу, стоящему в правой части формулы (6.8), можно применить теорию вычетов. Поэтому справедлива
76

75 |
www.studhelp.info |
Теорема 6.7. Если a1, a2 ,..., am – особые точки функции F(z) в области
| z |≤ R0 = es0 , то
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (n) = åRes F(z)z n−1 . |
|
|
|
|
|
|
|
|
(6.9) |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k=1 |
|
ak |
|
|
|
|
|
P(z) |
|
|
|
|
|
|
|
|
|
|
||||||||
Замечание. |
Если, |
|
в |
частности, |
|
|
F(z) = |
|
– |
несократимая дробь и |
|||||||||||||||||||||||||||||||||
|
Q(z) |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
fo |
|||||
a1, a2 ,..., am – простые корни знаменателя Q(z), то |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
P(ak ) |
|
an−1 . |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
f (n) = å |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Напомним, что |
|
|
|
|
|
|
|
|
|
k=1Q'(ak ) |
|
|
k |
|
|
|
|
|
|
i |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
||||||||||
а) если а – простой полюс, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Res F(z)zn−1 = lim F(z)zn−1(z − a); . |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
z→a |
|
|
|
|
|
|
|
|
|
|
n−1Pl |
|
|
|
|
|||||
б) если а – полюс кратности l , то |
|
|
|
|
|
|
|
|
l−1 |
[F(z)z |
]. |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
Res F(z)z n−1 = |
|
1 |
|
|
|
|
|
lim |
d |
|
|
|
|
|
l−1 |
(z − a) |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
(l − 1)! z→a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
||||||||||||||
|
|
|
|
|
+ lim |
|
|
|
|
|
|
UDH= + . |
|
|
dz |
|
|
|
|
|
|
|
|
||||||||||||||||||||
Рассмотрим примеры. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
||||||||||||||||
пº9. F(z) = |
|
|
z + 1 |
|
= |
|
|
z + 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
. Найти |
f (n) . |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
z2 + 2z + 3 |
(z −1)(z + 3) |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
Точки z1 = 1, z2 = 3 – простые полюса. Поэтому |
|
(z + 1)z n−1 |
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
f (n) = Res F(z)z n−1 + Res F(z)z n−1 = lim |
+ |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
z=3 |
|
|
|
|
|
|
|
|
|
z→1 |
|
z + 3 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
z=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
(z + 1)z n−1 |
|
|
1 |
|
|
|
|
(−3)n−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
S |
− 1 |
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
z→3 |
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
пº10. F(z) = |
|
z |
+ |
3 |
|
. Найти f (n) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
www |
|
−1) |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
(z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Здесь z =1 – особая точка, полюс 3-го порядка. Поэтому |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
f (n) = |
1 |
lim |
[F(z)z n−1 |
(z − 1)3 ]'' |
= |
1 |
|
lim [(z + 3)z n−1]'' |
= |
1 |
lim [z n + 3z n−1]'' = |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
2! z→1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 z→1 |
|
|
|
|
|
|
|
|
|
|
|
|
2 z→1 |
|
|
|
|
|||||||||
= |
1 |
lim [n(n − 1)z n−2 |
+ 3(n − 1)(n − 2)z n−3 |
]= |
|
1 |
|
(n − 1)(n + 3n − 6) = (n − 1)(2n − 3). |
|||||||||||||||||||||||||||||||||||
|
2 |
|
|||||||||||||||||||||||||||||||||||||||||
|
2 z→1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
▲
6.4. Решение разностных уравнений и систем разностных уравнений с помощью Z -преобразования
Рассмотрим приложения Z -преобразования к решению линейных разностных уравнений (РУ). Линейные разностные уравнения получаются из линейных
77

|
|
|
|
|
|
|
76 |
|
|
www.studhelp.info |
||
дифференциальных уравнений для импульсных (или решетчатых) функций. |
||||||||||||
Например, пусть даны уравнения |
y'= f (x) , |
|
|
(6.10) |
|
|||||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
y''+ay'+by = f (x) . |
|
|
(6.11) |
|
|||
Считаем, что |
y(x) – решетчатая функция, т.е. она задается таблицей значе- |
|||||||||||
ний в равноотстоящих узлах с шагом h =1. |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
y |
2 |
|
y1 = y2 |
− y1 |
|
|
y''(xn ) |
|
fo |
||
xn |
y(xn ) |
|
y'(xn ) |
|
|
|
|
|
||||
0 |
y0 |
|
y0 = y1 − y0 |
|
2 y0 = y1 − y0 = ( y2 − y1) − (y1 − y0 ) = |
|
||||||
1 |
y1 |
|
|
|
||||||||
|
|
= y2 − 2y1 + y0 |
.i |
|
|
|||||||
|
|
3 |
|
|
|
|
|
|
||||
|
|
|
|
|
… |
|
|
|
||||
|
|
|
|
y2 = y3 − y2 |
|
|
|
n |
|
|||
3 |
y |
|
|
|
|
|
||||||
|
|
|
|
… |
|
|
|
|
|
|
|
|
… |
… |
|
|
|
2 yn−1 = |
L |
|
|
|
|||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||
n |
yn−1 |
|
yn−1 = yn − yn−1 |
|
yn − |
yn−1 = ( yn+1 |
− yn ) − |
|
||||
|
|
|
|
|
|
|
E |
|
|
|
|
|
n-1 |
yn |
|
yn = yn+1 − yn |
|
− ( yn − yn−1) = ynP+1 − 2yn + yn−1 |
|
||||||
n+1 |
yn+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
UDH |
|
|
|
|
|
|
Разности 1-го порядка |
y0, y1,..., |
yn при шаге h =1 |
приближают производ- |
|||||||||
ные 1-го порядка, а разности 2-го – производные 2-го порядка. |
|
|
|
|||||||||
Уравнение (6.10) в узле n перепишется так: |
|
|
|
|
|
|||||||
|
|
|
|
|
y(n + 1) − y(n) = f (n) |
|
|
(6.12) |
|
|||
(6.12) – линейное разностное уравнение первого порядка. |
|
|
|
|||||||||
|
|
|
|
T |
|
|
|
|
|
|
|
|
Дифференциальное уравнение (6.11) в n -ом узле имеет вид: |
|
|
|
|||||||||
|
y(n + 2) − 2y(n + 1) + y(n) + a[y(n + 1) − y(n)] + by(n) = f (n) . |
(6.13) |
|
|||||||||
(6.13) – линейное разностное уравнение второго порядка.
Итак, каждое линейное дифференциальное уравнение всегда можно свести к соответствующему линейному разностному уравнению.
Теперь обсудим вопрос о том, как в общем случае решать линейные разност- |
|||||
www |
|
|
|
|
|
ные уравнения.k S-го порядка. |
|
|
|||
Задача 2. Дано линейное разностное уравнение |
|
||||
L[ y] = A0 y(n + k) + A1y(n + k − 1) + A2 y(n + k − 2) + ... + Ak y(n) = f (n)(6.14) |
|||||
при начальных условиях |
|
|
|
||
|
|
y(0) = y0 , y(1) = y1,..., y(n − 1) = yn−1, |
|
||
где y0, y1,..., yn−1 – заданные числа. |
|
|
|||
Найти |
всю |
|
бесконечную |
последовательность |
значений |
y(n), y(n + 1), y(n + 2),... . |
|
|
|
||
Приступая к решению этой задачи, полагаем, что f (n) ↔ F(z) , |
y(n) – ре- |
||||
шетчатый оригинал, а Y (z) – его Z -изображение. Имеем: |
|
||||
78
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
77 |
|
|
|
|
|
|
|
|
|
|
|
www.studhelp.info |
||
|
|
y(n) ↔ Y (z), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
y(n + 1) ↔ z[Y (z) − y0 ], |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
y(n + 2) ↔ z 2 [Y (z) − ( y0 + y1 / z)], |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
...................................................... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
y(n + k − 1) ↔ z k −1[Y (z) − (y |
0 |
+ y / z + y 2 / z 2 + ... + y |
k−2 |
/ z k −2 )], |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
y(n + k) ↔ z k [Y (z) − ( y0 + y1 / z + y2 / z 2 + ... + yk−1 / z k −1)]. |
|
|
|
||||||||||||||||||||||||||
|
Теперь, комбинируя оригиналы, стоящие слева, |
с коэффициентами Ak ,..., A0 , |
|||||||||||||||||||||||||||||
в силу линейности соответствия получим комбинацию их Z -изображений с те- |
|||||||||||||||||||||||||||||||
ми же коэффициентами: |
|
|
k−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k−1 |
|
|
fo |
|||||||||
|
L[ y] ↔ Y (z)(A0 z |
k |
+ A1z |
+ Ak−1z + Ak ) |
− y0 (A0 z |
k |
+ A1z |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
+ Ak−1z) − |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|||
|
− y (A z k−1 |
+ A z k−2 |
+ A |
|
|
|
z) − ... − y |
|
|
A z. |
|
|
|
|
i |
|
|
||||||||||||||
|
|
−2 |
k−1 |
|
|
. |
|
|
|
||||||||||||||||||||||
1 |
0 |
1 |
|
|
|
k |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|||||||||||
|
Замечаем, что коэффициент при |
y0 получается просто отбрасыванием сво- |
|||||||||||||||||||||||||||||
бодного коэффициента при Y (z) . Коэффициент при |
yi |
получается из коэффи- |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
||
циента при yi−1 делением на z и отбрасыванием свободного члена. |
|
|
|
||||||||||||||||||||||||||||
|
Так как должно быть тождество (6.14) решетчатыхLоригиналов, то должны |
||||||||||||||||||||||||||||||
совпадать и их Z -изображения. Итак, получаем операторное Z -изображение: |
|||||||||||||||||||||||||||||||
|
L[ y] ↔ Y (z)(A z k |
+ A z k−1 + A |
z + A ) −Ey (A z k |
+ A z k−1 |
+ A |
|
z) − |
||||||||||||||||||||||||
|
|
|
0 |
|
1 |
|
|
|
|
|
|
k−1 |
|
|
k |
|
|
|
0 |
0 |
|
1 |
|
|
|
k−1 |
|
||||
|
− y (A z k−1 |
+ A z k−2 |
+ A |
|
−2 |
z) − ... − y |
k−1 |
A z ≡ F(z). |
|
|
|
|
|
|
|
||||||||||||||||
1 |
0 |
1 |
|
|
|
k |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
(6.15) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уравнение (6.15) легко решается относительно Y (z) . Запишем его так: |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
Y (z)ϕ(z) − ψ(z) ≡ F(z), |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
Y (z) = |
|
F(z) + ψ(z) |
. |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
UDH |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Остается только стандартнымT |
|
|
|
|
ϕ(z) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
путем через вычеты |
восстановить решетчатый |
|||||||||||||||||||||||||||||
оригинал y(n) |
|
|
|
|
|
|
|
|
|
|
|
▲ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Аналогично.решаютсяS |
|
системы линейных разностных уравнений. |
|
|
|
|||||||||||||||||||||||||
|
Рассмотрим пример. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
пº11. Дано: РУ второго порядка |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
y(n + 2) − y(n) = 2n |
|
|
|
|
|
|
|
(6.16) |
|||||||||||||||
при начальных условиях y(0) = y(1) = 0 . Найти y(n) . |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
Пусть |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
www |
|
|
|
|
|
|
|
y(n) ↔ Y (z). |
|
|
|
|
|
|
|
|
|
|
(6.17) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Тогда |
|
y(n + 2) ↔ z2[Y (z) − (y |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
0 |
+ y / z)]. |
|
|
|
|
(6.18) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||
Комбинируя соотношения (6.17) и (6.18) с коэффициентами -1, 1 уравнения (6.16) и учитывая, что выражение y0 + y1 / z равно нулю в силу начальных ус-
ловий, получим:
79

|
|
|
|
78 |
|
|
|
|
|
|
|
|
|
|
|
|
www.studhelp.info |
||||||
для левой части (6.16): y(n + 2) − y(n) ↔ Y(z)(z2 − 1); |
|
|
|
|
|
|
|
|
|
||||||||||||||
для правой части (6.16): 2n « |
|
z |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
- 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Операторное уравнение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
||||
|
Y (z)(z |
2 -1) = |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
имеет решение |
|
z |
- 2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y (z) = |
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
||||
|
(z2 -1)(z - 2) |
|
|
|
|
|
|
|
|
|
|||||||||||||
Здесь особые точки z1 = 1, z2 = −1, z3 = 2. Тогда по формуле (6.9) находим: |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
(-1) |
|
|
fo |
||
y(n) = ResY (z)zn−1 + Res Y (z)zn−1 + ResY (z)zn−1 = - |
+ |
|
+ |
2 |
. ▲ |
||||||||||||||||||
|
|
|
|||||||||||||||||||||
z=1 |
z=−1 |
|
|
|
|
|
|
|
z=2 |
|
|
|
|
2 |
|
|
n |
||||||
|
|
|
|
|
|
|
|
|
|
|
i6 |
3 |
|
||||||||||
пº12. Дано линейное разностное уравнение 2-го порядка . |
|
|
|
||||||||||||||||||||
|
y(n + 2) − 5y(n + 1) + 6y(n) = 1 |
P |
|
|
(6.19) |
||||||||||||||||||
при начальных условиях y(0) =1, y(1) = −1. Найти y(n) . |
|
|
|
|
|
||||||||||||||||||
D Пусть |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
y(n) ↔ Y (z). |
|
|
|
|
L |
|
|
|
|
(6.20) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
E |
|
|
|
|
|
|
|||||||||||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
y(n + 1) ↔ z[Y (z) − y0 ] = z[Y (z) − |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
1]; |
|
|
|
|
|
|
|
|
(6.21) |
||||||||||||||
y(n + 2) « z 2[Y (z) - y |
|
- y |
|
/ z] = z 2[Y (z) - 1 + |
1/ z] |
|
|
||||||||||||||||
0 |
1 |
|
|
|
|
|
|||||||||||||||||
|
UDHz |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Умножая формулы (6.20) – (6.21) соответственно на 6, -5, 1, получим: y(n + 2) - 5y(n + 1) + 6y(n) « Y (z)[z 2 - 5z + 6] - (z 2 - 5z) + z.
Для правой части уравнения (6.19), будем иметь: |
|
|
|||||||||||||
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
1 « |
|
|
. |
|
|
|
|
||||||
|
z -1 |
|
|
||||||||||||
Операторное уравнение |
|
|
|
|
|
|
1 |
|
5 |
||||||
www |
|
|
|
|
|
|
|
|
|
||||||
. Y (z)[z |
2 |
- 5z + 6] - (z |
2 |
- 5z) + z = |
z |
|
|
||||||||
|
|
z -1 |
|
|
|
||||||||||
имеет решение |
|
|
z3 - 7z2 + 7z |
|
|
|
z3 - 7z2 + 7z |
|
|
||||||
|
Y (z) = |
|
= |
|
|
|
. |
||||||||
|
(z -1)(z2 - 5z + 6) |
|
|
|
(z -1)(z - 2)(z - 3) |
||||||||||
Функция Y (z) представляет собой несократимую дробь, |
знаменатель кото- |
||||||||||||||
рой имеет простые корни z1 = 1, z2 = 2, z3 = 3. Тогда по формуле (6.9) находим:
y(n) = ResY (z)z n−1 + ResY (z)z n−1 + ResY (z)z n−1 |
= |
|
+ 3 × 2n - |
|
× 3n. |
||||||||||
2 |
2 |
||||||||||||||
z=1 |
z=2 |
|
z=3 |
|
|
|
|
|
|
||||||
Проверим, выполняются ли начальные условия: |
|
|
|
|
|
|
|
|
|||||||
y(0) = |
1 |
+ 3 - |
5 |
=1, y(1) = |
1 |
+ 6 - |
15 |
|
= -1. |
|
|
||||
2 |
2 |
|
|
2 |
|
|
|
||||||||
|
|
2 |
|
|
|
|
|
|
|
||||||
80

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
79 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
www.studhelp.info |
||||
|
Значит, функция |
y(n) = |
|
1 |
+ 3 × 2n - |
5 |
|
|
× 3n |
|
является решением исходной зада- |
||||||||||||||||||||||||||||||||||
2 |
|
||||||||||||||||||||||||||||||||||||||||||||
чи. ▲ |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
пº13. Решить систему линейных разностных уравнений |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
ì |
|
|
|
|
|
- x(n) - y(n) = 3 |
n |
, |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ïx(n + 1) |
|
|
|
|
|
|
|
|
|
(6.22) |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
í |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
ï |
|
|
|
|
|
+ 2x(n) = -3 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
îy(n + 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
fo |
|||||||||||||||||
при начальных условиях x(0) = 3, y(0) = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
D Пусть x(n) |
– решетчатый оригинал, а |
|
X (z) – его Z-изображение. Тогда с |
|||||||||||||||||||||||||||||||||||||||||
учетом начальных условий будем иметь |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x(n) ↔ X (z); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
x(n + 1) « z[X (z) - x(0)] = z[X (z) - 3)] |
. |
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
Аналогично |
|
|
|
|
|
y(n) ↔ Y (z), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
y(n + 1) « z[Y (z) - y(0)] = zY(z), |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3n « |
|
|
z |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
z |
- 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Операторная Z-система, соответствующая системе (6.22), выглядит так: |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
í |
|
|
UDHz - 3 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ìz[X (z) - 3] - X (z) |
|
+ YE(z) = |
|
z |
, |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z - 3 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
í |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
ïzY (z) + 2X (z) = - |
|
z - |
3 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
или |
|
|
|
|
î |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
Tï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
ì |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3z |
- 8z |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ï(z -1)X (z) + Y (z) |
= |
|
|
|
, |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
. |
|
|
|
ï2X (z) + zY (z) = - |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
î |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z - 3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Решая последнюю систему по правилу Крамера, получим: |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
www |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
3z |
|
- 8z |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
z - 3 |
|
|
|
|
|
3z3 - 8z |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
- |
|
|
z |
|
z |
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
z(3z2 - 8z +1) |
|
|
|
|
|
|
||||||||||||||||||||||
z - 3 |
|
|
|
|
|
z - 3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
X (z) = |
|
|
|
= |
|
|
z - 3 |
= |
|
|
|
|
|
; |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
z -1 |
1 |
|
|
|
|
|
|
|
|
|
(z - 3)(z +1)(z - |
2) |
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
z2 - z - 2 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
2 |
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
81

|
|
|
|
|
|
|
|
|
|
|
|
80 |
|
|
www.studhelp.info |
|
|
z -1 |
|
3z 2 - 8z |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
z - 3 |
|
|
z - z 2 - 6z 2 + 16z |
|
|
|
|||
|
|
2 |
|
- |
z |
|
|
|
17z - 7z 2 |
||||||
|
|
|
z - 3 |
|
|
|
|
|
|||||||
Y (z) = |
|
|
|
|
|
z - 3 |
|
||||||||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
= |
|
= |
|
. |
|||||
|
|
z -1 1 |
|
|
|
z 2 - z - 2 |
(z - 3)(z + 1)(z - 2) |
||||||||
|
|
|
|
||||||||||||
|
|
2 |
|
|
z |
|
|
|
|
|
|
|
|
||
Осталось по данным Z-изображениям X (z) и Y (z) восстановить решетчатые оригиналы. Используя формулу (6.9) и вычисляя вычеты в простых полюсах
z1 = −1, z2 = 2, z3 = 3, получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
fo= |
|||||||||||||||||||||||||
|
x(n) = lim |
|
(3z 2 - 8z + 1)z n |
+ lim |
(3z 2 - 8z + 1)z n |
|
+ lim |
(3z 2 - 8z + 1)z |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
z→−1 |
|
|
(z - 2)(z - 3) |
|
|
|
|
z→2 |
(z + 1)(z - |
3) |
|
|
|
z→3 |
(z |
+ 1)(z - 2) |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
3 + 8 + 1 |
|
|
|
|
n |
|
|
12 - 16 + 1 |
|
n |
|
|
|
27 - 24 + 1 |
|
n |
|
|
|
|
|
n |
|
|
|
n |
i |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
||||||||||||||||||||||||||||||||
= |
|
|
|
|
(-1) + |
|
|
|
|
|
|
|
|
|
|
|
2 + |
|
|
|
|
|
|
|
|
|
3 = (-1) + |
2 |
. |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
12 |
|
|
|
|
|
- 3 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
+ 3 ; |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
(17 - 7z)z n |
|
|
|
|
|
|
|
|
(17 - 7z)zn |
|
|
|
|
|
(17 - 7z)z n |
|
|
|
||||||||||||||||||||||||||||
|
y(n) = |
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ lim |
|
|
|
|
|
|
|
|
|
|
|
|
+ lim |
|
|
|
|
|
P= |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
z→−1 |
(z - 2)(z |
- 3) |
|
|
|
z |
→2 |
|
(z +1)(z - 3) |
|
z→3 |
(z +1)(z - 2) |
|
|
|||||||||||||||||||||||||||||||||||||
|
= 2(-1)n - 2n - 3n. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
||||||||||||||||||||
|
Сделаем контрольную проверку начальных условий: |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x(0) =1 + 1 + |
|
|
|
|
|
|
|
|
E |
= 0 . |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 = 3, y(0) = |
2 |
− |
1 |
−1 |
|
|
|
|
|
|||||||||||||||||||||||||||
|
Начальные условия выполняются. Следовательно, функции |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x(n) = (-1)n + 2n + 3n , y(n) = 2(-1)n - 2n - 3n |
|
|
|||||||||||||||||||||||||||||||||||||||
|
являются решением исходной задачи. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
▲ |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задачи для самостоятельного решения |
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
UDH |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
Задача 1. Найти Z-преобразование для данных решетчатых функция: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Tn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
а) f (n) = 1; б) f (n) = |
(−1) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
Задача 2. Восстановить последовательность |
f (n) по ее Z-преобразованию. |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
F(z) = |
1 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
z - a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Задача 3. Решить уравнение: x(n + 2) − 5x(n + 1) + 6x(n) = 0, x(0) = 1, x(1) = 2. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Отв.: |
x(n) = 2n. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Задача 4. Решить систему разностных уравнений: |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
x(n + 2) − x(n + 1) − x(n) = 0, x(0) = 0, x(1) = 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
www1 |
æ |
æ1 |
|
|
|
|
ö |
n |
|
|
|
æ |
|
|
|
|
|
ö |
n |
ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
+ |
5 |
|
|
|
1 - |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
ç |
|
|
|
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ç |
|
|
|
|
|
|
÷ |
|
|
|
|
ç |
|
|
|
|
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Отв.: x(n) = |
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
ç |
ç |
|
2 |
|
|
÷ |
|
ç |
2 |
|
÷ |
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
5 |
è |
|
|
|
ø |
|
|
|
|
è |
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
82
