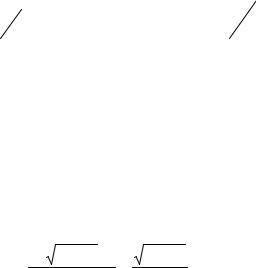
где ψλ = ∫λ(t)dt .
Из (4.1) и (4.2) следует, что Р0 вых для прямых видов модуляции не зависит от частоты, а для интегральных возрастает прямо пропорционально квадрату частоты. Последнее объясняется тем, что при (Рс/Рш)>>1 эффективное напряжение на выходе частотного детектора пропорционально девиации частоты, а его квадрат – квадрату частоты.
Чтобы определить дисперсию (мощность) шума на выходе приемника, необходимо учесть все шумовые составляющие в пределах выходной полосы Fвых = Fмакс . В соответствии с этим для непрерывных методов модуляции
(АМ, ЧМ, ФМ) будем иметь
Pш.вых= σш2 |
.вых = ∫ Р0 выхdf = |
∫ Р0 выхdf . |
(4.3) |
|
Fвых |
Fмакс |
|
Для импульсных видов модуляции (АИМ, ФИМ, ШИМ)
F |
= 1 |
2Т |
и |
P |
= |
Р0 вых |
. |
(4.4) |
вых |
|
|
ш.вых |
|
2Т |
|
|
Поскольку в теории потенциальной помехоустойчивости приняты пределы изменения информационного параметра λ(t) от –1 до +1, а мощность шума на выходе приемника равна дисперсии абсолютной ошибки и связана с приведенной среднеквадратичной ошибкой соотношением
Pш.вых = D( λ) = δср2 .кв(λмакс − λмин)2 ,
то
δср.кв = |
Pш.вых |
= |
Pш.вых . |
(4.5) |
|
λмакс − λмин |
|
2 |
|
Таким образом, можно предложить следующий порядок получения выражений приведенной среднеквадратичной ошибки для различных видов модуляции:
–записывается выражение для соответствующего вида модуляции;
–находится частная производная ∂S(λ, t) / ∂λ для прямых видов модуля-
ции и − ∂S(λ, t) / ∂ψλ для интегральных видов модуляции;
–находится I среднее значение квадрата частной производной;
–по выражению (4.1) или (4.2) находится спектральная плотность шума на выходе приемника;
–определяется мощность шума на выходе приемника из выражения (4.3);
107
– находится приведенная среднеквадратичная ошибка по выражению
(4.5).
4.2. Помехоустойчивость непрерывных методов модуляции
4.2.1. Потенциальная помехоустойчивость АМ. При АМ сигнал имеет
вид
S(λ, t) = U0 (1 + mλ(t)) cos ω0t .
Находим частную производную
∂S(λ,t) |
=U0mcosω0t , |
∂λ |
|
а среднее значение квадрата этой величины (средняя мощность)
|
1 T |
2 |
|
U 2 |
|
2 при |
ω0 |
|
1 |
. |
||
I = |
|
∫(U0mcosω0t) |
|
dt = |
0 |
|
|
>> |
|
|
||
T |
|
m |
2π |
T |
||||||||
|
0 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Согласно выражению (4.1) спектральная плотность шума на выходе приемника
P |
|
= |
|
2P0 вх |
|
= |
|
P0 вх . |
|
|
|
||||
0 вых |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
U |
2m2 |
P m2 |
|
|
|
|||||||||
|
|
|
|
|
0 |
|
|
|
|
|
c |
|
|
|
|
Поскольку она не зависит от частоты, то при Fвых = Fмакс |
из выражения |
||||||||||||||
(4.3) получим |
|
|
|
Р0 вх |
|
|
|
P0 вхFмакс |
|
||||||
|
|
|
|
|
|
|
|
||||||||
Pш.вых= |
∫ |
|
|
df |
= |
|
|
. |
|
||||||
|
P m2 |
|
P m2 |
|
|||||||||||
|
F |
|
|
c |
|
|
|
|
|
|
c |
|
|
|
|
|
макс |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда из выражения (4.5) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
δср.кв |
= |
1 |
|
|
P0 |
вхFмакс |
. |
|
(4.6) |
||||||
2m |
|
|
|
Pc |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
4.2.2. Потенциальная помехоустойчивость ФМ. Сигнал на входе при-
емника имеет вид
S(λ,t) =U0 cos(ω0t + mϕλ(t)) ,
где mϕ – индекс фазовой модуляции.
108
Тогда
∂S∂(λt ,t)= −U0mϕ sin(ω0t + mϕλ(t))
и
|
|
1 |
T |
2 2 |
|
|
I = |
∫ |
(−U0mϕ sin(ω0t + mϕλ(t))2 dt = |
U0 mϕ |
. |
||
T |
|
|||||
|
0 |
2 |
|
|||
|
|
|
|
|
|
|
Согласно выражению (4.1)
P |
вых |
= |
P0 вх |
, |
0 |
|
P m2 |
|
|
|
|
|
c ϕ |
|
а мощность на выходе приемника в соответствии с выражением (4.3)
P |
ш.вых |
= |
∫ |
Р |
df = |
P0вхFмакс |
. |
|
|||||||
|
|
0 вых |
|
P m2 |
|||
|
|
|
F |
|
|
c ϕ |
|
|
|
|
макс |
|
|
|
|
Тогда
δ |
ср.кв |
= 1 |
P0 вхFмакс . |
(4.7) |
|
2mϕ |
Pc |
|
|
|
|
|
Заметим, что увеличение индекса модуляции mϕ обеспечивает уменьшение ошибки без увеличения мощности сигнала. Однако это имеет место до тех пор, пока отношение сигнал/шум на входе детектора значительно больше единицы.
4.2.3. Потенциальная помехоустойчивость ЧМ. Сигнал на входе при-
емника имеет вид
S(λ,t) =U0 cos(ω0t + ∫ωДλ(t)dt) ,
где ωД – девиация частоты.
Частотная модуляция относится к интегральным видам, а поэтому частная производная будет
∂S(λ,t)
∂ψλ = −U0ωД sin(ω0t + ωд∫λ(t)dt) .
Среднее значение этой производной
109