режиме в (1+mАМ)2 раз больше мощности молчания. Ширина спектра АМ сигнала зависит от величины максимальной частоты модуляции и равна 2Ωmax.
Для ЧМ-сигналов средняя за период высокой частоты мощность постоянна, так как амплитуда колебаний неизменна (Uω1.= const). Ширина спектра ЧМ-сигнала, равна 2ωg, зависит только от амплитуды модулирующего сигнала и не зависит от его частоты.
Для ФМ-колебаний средняя за период высокой частоты мощность также неизменна, ибо Uω1 = const. Ширина спектра равна 2mΩ = 2ωg, и зависит как от амплитуды модулирующего сигнала, так и от его частоты.
Таким образом, практическая ширина спектра колебаний с угловой модуляцией в m раз больше ширины спектра АМ-колебаний.
2.4.Одновременная модуляция по амплитуде и по частоте
Вряде случаев возникает необходимость в передаче двух сообщений с помощью одного носителя. Тогда одним сообщением носитель модулируют по частоте, а другим – по амплитуде. Наиболее простой по составу спектр сигнала
сдвойной модуляцией получится при гармоническом законе изменения, как частоты, так и амплитуды. Пусть по частоте носитель модулируется сообщени-
ем с частотой Ω1, а по амплитуде – с частотой Ω2. Тогда частота и амплитуда носителя будут изменяться в соответствии с выражениями
ω(t) = ω + ω cosΩt |
, |
(2.37) |
||
1 |
g |
1 |
|
|
U(t) = U ω1(1 + mАМ cos Ω2t). |
(2.38) |
|||
Модулированное по частоте напряжение было получено выше при постоянной амплитуде Uω1 (2.31). При изменении амплитуды в этом выражении следует заменить постоянную амплитуду Uω1 изменяющейся в соответствии с (2.38). Тогда получим:
U(t) = U (1 |
+ m |
ÀÌ |
cos ѓ¶ t)(J |
(m)cos ѓЦt − J (m)cos(ѓЦ − ѓ¶ )t + |
|||||
ѓЦ1 |
|
2 |
0 |
1 |
1 |
1 |
|
1 |
|
+ J (m)cos(ѓЦ + ѓ¶ )t + J (m)cos(ѓЦ − 2ѓ¶ )t + J |
(m)cos |
(ѓЦ + 2ѓ¶ )t + ...). |
|||||||
1 |
1 |
1 |
2 |
1 |
|
1 |
2 |
1 |
1 |
По сравнению с напряжением, модулированным только по частоте, здесь появляются дополнительные составляющие двух видов:
m |
AM |
U |
ω1 |
J (m)cosωt cosΩ t = |
mAM |
U |
ω1 |
J (m)cos(ω ±Ω )t |
(2.39) |
|||
|
||||||||||||
|
|
0 |
1 |
2 |
2 |
|
0 |
1 2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
и
m |
AM |
U |
ω1 |
J |
(m) cos (ω ± nΩ )t cos Ω |
t = |
m AM |
U |
ω1 |
J |
(m) × |
||
|
|||||||||||||
|
|
n |
1 |
1 |
2 |
2 |
|
n |
(2.40) |
||||
|
|
|
|
|
|
|
|
|
|
|
|||
×( cos (ω1 ± nΩ1 + Ω2 )t + cos (ω1 ± nΩ1 − Ω2 )t).
36
Чтобы яснее выявить спектральный состав сигнала, предположим сначала, что Ω1>>Ω2, т.е. изменение амплитуды происходит значительно медленнее, чем изменение частоты. Тогда можно считать, что в спектре частотномодулированного сигнала около несущего колебания с частотой ω1 и боковых составляющих с частотами ω1±nΩ1 появилось дополнительно по два спутника с частотами, отличающимися на ±Ω2. Спектр такого сигнала показан на рис. 2.14.
∆ωАМ/2 |
∆ωЧМ |
∆ωАМ/2 |
1 |
1 |
-Ω |
1 |
+Ω |
2 |
1 |
2 |
-Ω |
1 |
+Ω |
1 |
+ |
Ω |
- |
n-Ω |
2 |
Ω- |
2 |
Ω- |
ω |
+Ω |
2 |
+Ω |
2 |
+nΩ |
1 |
|
n-Ω |
1 |
1 |
1 |
1 |
|||||||||
1 |
1 |
-Ω |
1 |
-Ω |
1 |
1 |
+Ω |
1 |
+Ω |
1 |
+nΩ |
||
ω |
ω |
ω |
ω |
ω |
ω |
|
ω |
ω |
ω |
ω |
ω ω |
|
|
|
|
1 |
|
1 |
|
|
|
1 |
|
1 |
|
1 |
|
Рис. 2.14. Спектр сигнала при одновременной модуляции по частоте и амплитуде при Ω1>>Ω2
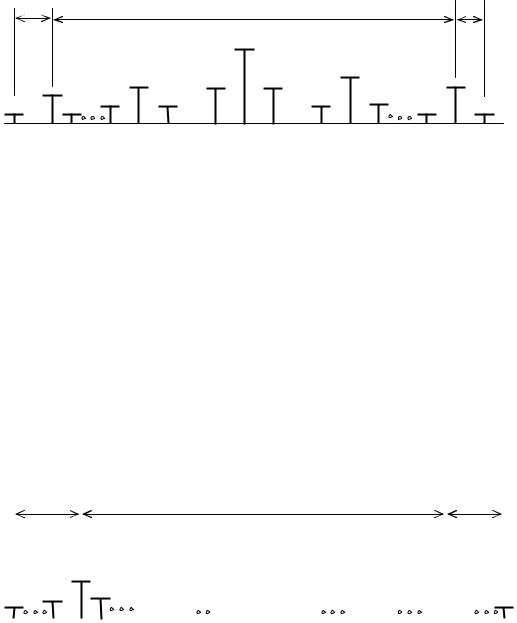
Для систем телемеханики интерес представляет второй случай, а именно спектр сигнала при Ω1<<Ω2. Тогда можно считать, что у каждой из трех спектральных линий АМ сигнала (несущей с частотой ω1, нижней (ω1-Ω2) и верхней (ω1+Ω2) боковых составляющих) появились дополнительно по две боковые дискретные полосы: верхняя с частотами +nΩ1 и нижняя с частотами -nΩ1. Спектр сигнала для этого случая двойной модуляции показан на рис. 2.15.
∆ωЧМ/2 |
|
|
|
|
|
|
∆ωАМ/2 |
|
|
|
∆ωЧМ/2 |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
2 |
- |
1 |
- |
nΩ1 |
1 |
ω |
1 |
+n |
2 |
n-Ω1 |
2 |
2 |
-Ω |
-Ω |
-Ω |
+Ω |
+Ω |
+Ω |
+Ω |
|||||||
ω |
ω |
ω |
Ω |
ω |
ω |
ω |
ω |
ω |
ω |
ω |
|||
1 |
1 |
1 |
+n Ω |
1 |
|
1 |
1 |
1 |
1 |
1 |
|
1 |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
Рис. 2.15. Спектр сигнала при одновременной модуляции по частоте и амплитуде при Ω1<<Ω2
37