
- •Вводная лекция
- •В.1 Определение, задачи и проблемы
- •В.2 Телемеханические устройства, комплексы и системы
- •В.3 Краткая историческая справка развития телемеханики
- •Часть 1. Сообщения и сигналы
- •СОДЕРЖАНИЕ
- •ВВЕДЕНИЕ
- •1. ОБЩИЕ СВЕДЕНИЯ О СИГНАЛАХ
- •1.1. Основные типы сигналов
- •1.2. Периодические сигналы
- •1.4. Спектр одиночного прямоугольного импульса
- •2. МОДУЛЯЦИЯ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
- •2.1. Амплитудная модуляция
- •2.2. Частотная модуляция (ЧМ)
- •2.3. Фазовая модуляция (ФМ)
- •2.4. Одновременная модуляция по амплитуде и по частоте
- •3. ИМПУЛЬСНАЯ МОДУЛЯЦИЯ
- •3.2. Фазоимпульсная модуляция (ФИМ)
- •3.3. Широтно-импульсная модуляция (ШИМ)
- •4. МАНИПУЛИРОВАННЫЕ СИГНАЛЫ
- •4.1. Амплитудная манипуляция (АМП)
- •4.2. Фазовая манипуляция (ФМП)
- •4.3. Частотная манипуляция (ЧМП)
- •4.4. Двукратная модуляция
- •4.5. Спектры радиоимпульсов
- •5. МОДУЛЯТОРЫ И ДЕМОДУЛЯТОРЫ
- •5.1. Амплитудные модуляторы
- •5.2. Детекторы АМ-сигналов
- •5.3. Модуляторы однополосного сигнала
- •5.4. Детекторы ОАМ-сигнала
- •5.5. Частотные модуляторы
- •5.6. Детекторы ЧМ-сигналов
- •5.7. Фазовые модуляторы
- •5.8. Фазовые детекторы (ФД)
- •5.9. Амплитудно-импульсные модуляторы
- •5.11. Широтно-импульсный модулятор
- •5.12. Демодуляторы ШИМ-сигналов
- •5.13. Фазоимпульсные модуляторы
- •5.14. Детекторы ФИМ-сигналов
- •5.15. Дискретный амплитудный модулятор
- •5.17. Модуляторы ЧМП-сигналов
- •5.19. Модуляторы ФМП-сигналов
- •5.20. Детекторы ФМП-сигнала
- •ЛИТЕРАТУРА
- •Часть 2. Коды и кодирование
- •СОДЕРЖАНИЕ
- •ВВЕДЕНИЕ
- •1. КОДЫ И КОДИРОВАНИЕ
- •1.1. Основные понятия
- •1.2. Цифровые коды
- •1.3. Простые двоичные коды
- •1.4. Оптимальные коды
- •2. КОРРЕКТИРУЮЩИЕ КОДЫ
- •2.1. Основные понятия
- •2.2. Коды с обнаружением ошибок
- •2.3. Коды с обнаружением и исправлением ошибок
- •2.4. Частотные коды
- •3. ТЕХНИЧЕСКИЕ СРЕДСТВА ПРЕОБРАЗОВАНИЯ ДЛЯ НЕПОМЕХОЗАЩИЩЕННЫХ КОДОВ
- •3.2. Дешифратор двоичного кода в десятичный код
- •3.3. Дешифратор двоично–десятичного кода в десятичный
- •3.4. Преобразователи двоичного кода в двоично–десятичный код и обратно
- •3.5. Преобразователь двоичного кода 8–4–2–1 в самодополняющийся двоично–десятичный код 2–4–2–1
- •3.6. Преобразователь самодополняющего двоично–десятичного кода 2–4–2–1 в двоичный код 8–4–2–1
- •3.7. Преобразователь кода Грея в двоичный код и обратно
- •3.8. Технические средства кодирования и декодирования эффективных кодов
- •3.9. Схемы равнозначности кодов
- •4.1. Кодер и декодер кода с защитой на четность
- •4.2. Кодер и декодер кода с постоянным весом
- •4.3. Кодер и декодер кода с двумя проверками на четность
- •4.4. Кодер и декодер кода с повторением
- •4.5. Кодер и декодер кода с числом единиц, кратным трем
- •4.6. Кодер и декодер инверсного кода
- •4.7. Кодер и декодер корреляционного кода
- •4.8. Кодер и декодер кода Бергера
- •4.10. Кодирующее и декодирующее устройство кода Хемминга
- •4.11. Технические средства умножения и деления многочлена на многочлен
- •4.12. Кодер и декодер циклического кода
- •4.13. Кодер и декодер итеративного кода
- •4.14. Кодер и декодер рекуррентного кода
- •5.1. Кодер и декодер кода на перестановки
- •5.2. Кодер и декодер кода на размещения
- •5.3. Кодер и декодер кода на сочетания
- •5.4. Дешифратор одночастотного кода
- •5.5. Кодер и декодер сменно–качественного кода
- •6. КОДЫ ДЛЯ ПЕРЕДАЧИ ЦИФРОВОЙ ИНФОРМАЦИИ ПО ПОСЛЕДОВАТЕЛЬНЫМ КАНАЛАМ СВЯЗИ
- •6.1. Методы кодирования
- •6.2. Шифратор и дешифратор кода Манчестер–2
- •ЗАКЛЮЧЕНИЕ
- •ЛИТЕРАТУРА
- •Часть 3. Линии связи и помехоустойчивость информации
- •СОДЕРЖАНИЕ
- •ВВЕДЕНИЕ
- •1. ЛИНИИ И КАНАЛЫ СВЯЗИ
- •1.1. Понятие о линии и канале связи
- •1.2. Способы разделения каналов
- •1.3. Проводные линии связи
- •1.4. Использование высоковольтных линий электропередачи (ЛЭП) в качестве линий связи
- •1.6. Радиолинии
- •1.7. Оптические линии связи
- •1.9. Структура линий связи
- •1.10. Сети передачи дискретных сообщений
- •1.11. Расчет основных характеристик цифровых линий связи
- •1.12. Расчет волоконно–оптической линии связи
- •2. ПОМЕХИ И ИХ ХАРАКТЕРИСТИКИ
- •2.1. Общие сведения о помехах
- •2.2. Математическое описание помехи
- •2.3. Виды искажений
- •3. ПОМЕХОУСТОЙЧИВОСТЬ ПЕРЕДАЧИ ДИСКРЕТНЫХ СООБЩЕНИЙ
- •3.1. Основные понятия
- •3.2. Помехоустойчивость передачи дискретных элементарных сигналов
- •3.3. Приём с зоной стирания
- •3.4. Помехоустойчивость двоичных неизбыточных кодов
- •3.5. Помехоустойчивость кодов с обнаружением ошибок
- •3.7. Помехоустойчивость систем с дублированием сообщений
- •3.8. Помехоустойчивость систем с обратными каналами связи
- •4. ПОМЕХОУСТОЙЧИВОСТЬ ПЕРЕДАЧИ НЕПРЕРЫВНЫХ СООБЩЕНИЙ
- •4.1. Общие соображения
- •4.2. Помехоустойчивость непрерывных методов модуляции
- •4.3. Помехоустойчивость импульсных методов модуляции
- •4.4. Потенциальная помехоустойчивость сложных видов модуляции
- •5. МЕТОДЫ ПОВЫШЕНИЯ ПОМЕХОУСТОЙЧИВОСТИ
- •5.1. Методы повышения помехоустойчивости передачи дискретных сообщений
- •5.2. Методы повышения помехоустойчивости передачи непрерывных сообщений
- •ЛИТЕРАТУРА
- •ПРИЛОЖЕНИЕ
Таким образом, спектр состоит из колебаний на несущей частоте ω1 и на боковых частотах ω1 ± kΩ , как в случае гармонического модулирующего сигнала C(t) = cosΩt , но амплитуды колебаний другие.
Примеры спектров ЧМП-сигналов, рассчитанных по выражению (4.14), показаны на рис. 4.8.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,64 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m=1,0 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
0,50 |
|
|
|
0,50 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
0,21 |
|
|
|
0,21 |
|
|
|
|
|
|
|
|
|
Q=2 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
0,04 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,04 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω |
|
|
4-Ω |
|
3-Ω |
|
|
2-Ω |
|
-Ω |
1 |
|
+Ω |
|
+2Ω |
|
|
|
|
+3Ω |
|
+4Ω |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
ω |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
1 |
|
1 |
|
1 |
1 |
|
|
|
|
1 |
|
1 |
|
|
|
1 |
1 |
|
|
|
|||||||||||||||||
|
ω |
|
ω |
|
|
ω |
|
ω |
|
|
|
|
ω |
|
ω |
|
|
|
|
ω |
|
ω |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
0,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,5 |
|
|
|
|
m=3 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q=2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
0,382 |
|
|
|
|
|
|
|
0,382 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
0,273 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,273 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,212 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
ω |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-5Ω |
|
-4Ω |
|
-3Ω |
|
-2Ω |
|
Ω- |
1 |
|
|
+Ω +2Ω |
|
+3Ω |
|
+4Ω |
+5Ω |
|
||||||||||||||||||
|
|
|
|
1 |
ω |
|
|
|
|||||||||||||||||||||||||||||
|
ω |
|
ω |
|
ω |
|
ω |
|
ω |
|
|
|
|
ω |
ω |
|
ω |
|
ω |
ω |
|
||||||||||||||||
1 |
|
1 |
|
1 |
|
1 |
|
|
|
|
|
|
|
|
1 |
|
1 |
|
1 |
1 |
|
1 |
|
||||||||||||||
Рис. 4.8. Примеры спектров ЧМП-сигналов
Из рис. 4.8 видно, что форма спектра сильно зависит от индекса модуляции и при индексах модуляции, близких к 1, основная энергия содержится в несущей и двух первых боковых. Отсюда можно сделать вывод, что ширина спектра ЧМП может быть определена из выражения
∆ωЧМП = 2(m +1)Ω . |
(4.15) |
В заключение следует отметить, что спектр становится несимметричным относительно несущей частоты при скважности, отличной от двух.
4.4.Двукратная модуляция
4.4.1.АМ-АМ-сигналы. Для повышения помехоустойчивости иногда модулированное (АМ, ЧМ) сообщение дополнительно модулируют по частоте
57
или амплитуде. Такой способ модуляции обозначается двумя индексами: первый означает способ модуляции поднесущей, второй – несущей. Кроме того, двукратная модуляция применяется при передаче сообщений по радиоканалам, а также в выделенной полосе частот проводной линии связи.
АМ-АМ-сигналы в телемеханике используются редко. Однако их шумовые характеристики часто служат эталоном для сравнения различных методов модуляции. Рассмотрим АМ-АМ-сигнал, когда промодулированная по амплитуде поднесущая описывается выражением
U АМ(t) =Uω1(1 + mАМ cos Ωt)sin ω1t , |
(4.16) |
где Uω1- амплитуда поднесущей; ω1 - круговая частота поднесущей; mAM- коэф-
фициент амплитудной модуляции на первой ступени;Ω- круговая частота модулирующего сообщения.
Сигнал U Н (t) является модулирующим по отношению к модулирующему колебанию
U Н (t) =U0 cosω0t . |
(4.17) |
В соответствии с определением амплитудной модуляции АМ-АМ-сигнал можно записать в виде
U АМ−АМ(t) =(U0 |
+ kUω1(1 + mАМ cosΩt)cosω1t)cosω0t = |
(4.18) |
|
=U0(1 + M AM (1 + mАМ cosΩt)cosω1t)cosω0t, |
|||
|
|||
где MAM=kUω1/U0 – коэффициент амплитудной модуляции на второй ступени.
Процесс получения АМ-АМ-сигнала показан на рис. 4.9.
Для получения спектра преобразуем выражение (4.18) и окончательно получим
U |
АМ −АМ |
(t) = U |
0 |
cos ω |
t + |
U 0 M AM |
cos( ω |
0 |
± ω )t + |
|
|||||||||
|
|
0 |
2 |
|
1 |
||||
|
|
|
|
|
|
|
|
||
+ |
U 0 M AM m AM |
cos( ω0 |
+ ω1 |
± Ω)t + |
(4.19) |
|
|
||||||
4 |
|
|
|
|
|
|
+ |
U 0 M AM m AM |
cos( ω |
0 |
− ω ± Ω)t. |
|
|
|
|
|||||
4 |
|
1 |
|
|
||
|
|
|
|
|
||
Согласно выражению (4.19) спектр АМ-АМ-сигнала имеет вид, представленный на рис. 4.10. Oн содержит составляющую на несущей частоте ω0 ,
две боковые составляющие на частотах ω0 + ω1 и ω0 − ω1, вокруг которых имеются по две составляющих на частотах ω0 + ω1 ± Ω и ω0 − ω1 ± Ω соответственно.
58
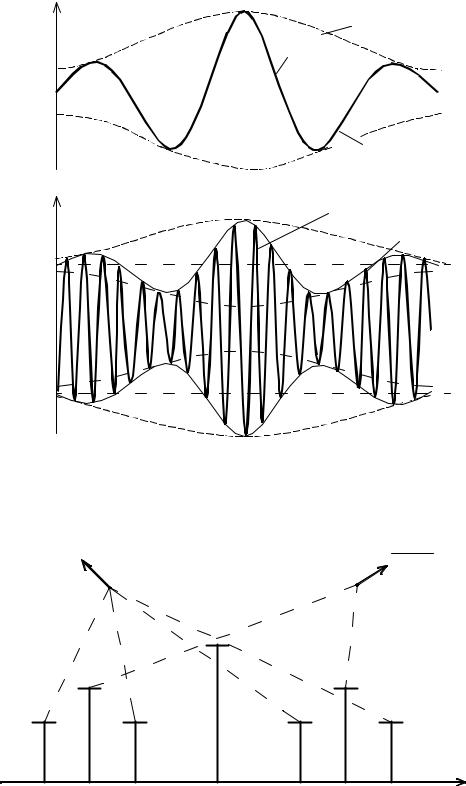
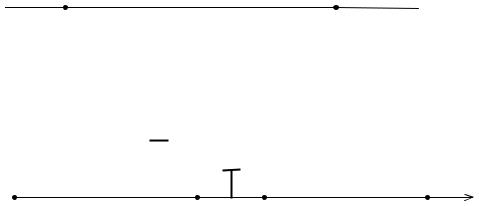
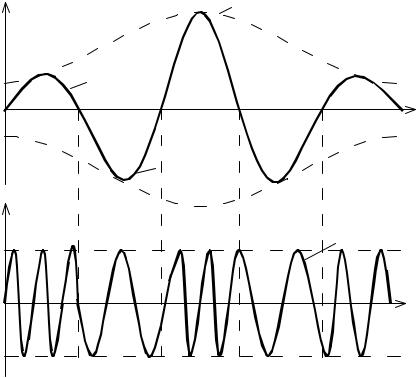
UАМ |
Сообщение |
|
АМ-сигнал |
0  t
t
 Поднесущая
Поднесущая
UАМ-АМ |
АМ-АМ-сигнал |
|
Несущая |
||
|
0  t
t
Рис. 4.9. Формы сигналов при АМ-АМ
UoM.m |
UoM |
4 |
2 |
|
|
|
U0 |
ω
ω0-ω1-Ωω0-ω1 ω0-ω1+Ω |
ω0 ω0+ω1-Ω ω0+ω1ω0+ω1+Ω |
Рис. 4.10. Спектр АМ-АМ-сигнала
Очевидно, что необходимая полоса частот для передачи такого сигнала определяется разностью частот верхней и нижней боковых составляющих, т.е.
59
∆ωAM −AM = ω0 + ω1 + Ω − ω0 + ω1 + Ω = 2(ω1 + Ω) , |
(4.20) |
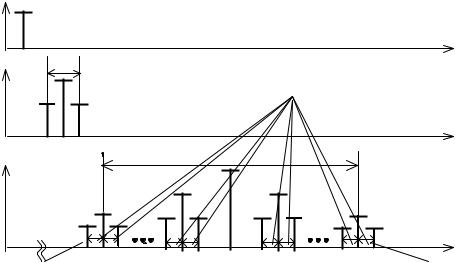
4.4.2. АМ-ЧМ-сигнал. При данном сигнале поднесущая промодулированная по амплитуде (4.16), модулирует носитель (4.17) по частоте. В соответствии с определением частотной модуляции можно записать выражение для АМ-ЧМ-сигнала, представленного на рис. 4.11, в виде
U АМ−ЧМ (t) =U0 cos(ω0t + kUω1 ∫(1 + mАМ cosΩt)cosω1tdt) . |
(4.21) |
UАМ C¦ t ¦ -сообщение
АМ-cигнал
t
Поднесущая
UАМ-ЧМ
Несущая
t
Рис. 4.11. Формы сигналов при АМ-ЧМ
Не раскрывая выражения (4.21), спектр АМ-ЧМ можно построить по следующему правилу: строится спектр полезного сообщения C(t), затем спектр полезного сообщения переносится на частоту поднесущей ω1 по правилам АМ
сигнала, а потом полученный спектр переносится на несущую частоту по правилам ЧМ-сигнала.
Спектр, построенный по рассмотренной выше методике, приведен на рис. 4.12. Следует отметить, что спектр, построенный по данной методике, дает представление о частотном составе спектра, позволяет определить полосу частот, занимаемую сигналом, но не дает возможности определить амплитуды отдельных гармонических составляющих.
60
UΩ
ω
Ω2Ω
UАМ |
Ω |
ω1-Ω ω1 ω1+Ω |
ω |
2ωgн |
|
UАМ-ЧМ |
|
|
ω |
ω0-nω1-Ω ω0-nω1 |
ω0-ω1 ω0 ω0+ω1 ω0+nω1 ω0+nω1+Ω |
Рис. 4.12. Процесс построения спектра АМ-ЧМ-сигнала
Определим полосу частот, занимаемую АМ-ЧМ-сигналом, как разность частот между верхней и нижней боковыми составляющими.
∆ωAM−AM =ω0 +nω1 +Ω−ω0 +nω1 +Ω= |
(4.22) |
=2(nω1 +Ω) ≈2(MЧМω1 +Ω) =2(ωgн +Ω), |
|
где МЧМ = ωg н /ω1 – индекс частотной модуляции несущего сигнала; ωgн – девиация частоты носителя.
4.4.3 ЧМ-АМ-сигнал. Частотно-модулированная поднесущая
UЧМ (t) =Uω1 cos(ω1t + mАМ sin Ωt)
модулирует носитель по амплитуде; в результате получаем ЧМ-АМ сигнал (рис. 4.13), который можно записать в виде
UЧМ−АМ (t) = (U0 + kUω cos(ω1t + mЧМ sin Ωt))cosω0t = |
|
|
|
1 |
|
=U0 |
(1 + M AМ cos(ω1t + mЧМ sin Ωt))cosω0t = |
(4.23) |
=U0 |
(1 + M AМ (cosω1t ×cos(mЧМ sin Ωt) − |
|
− sin ω1t ×sin(mЧМ sin Ωt))cosω0t.
61
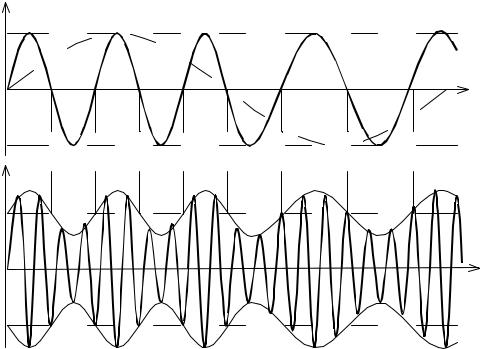
UЧМ(t) |
UС(t) |
|
t
UЧМ-АМ(t)
t
Рис. 4.13. Форма сигналов при ЧМ-АМ
Подставив в выражение (4.23) значения
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
cos(mЧМ sinΩt) = J0 (m) + 2 ∑ J 2n(m)cos2n Ωt |
|
|
||||||||||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
n=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ . |
|
|
|
|
|
|
|||
|
|
|
|
|
|
sin(mЧМ sinΩt) |
= |
|
|
|
Ω |
, |
|
|||||||
|
|
|
|
|
|
|
2 ∑(m) J 2n - 1 |
sin(2n - 1) t |
|
|
||||||||||
получим |
|
|
|
|
|
|
|
|
|
|
|
n=1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
UЧМ − АМ (t) =U0 (1 + M AМ (J0 (m)cosω1t + J1(m)cos(ω1 + Ω)t − |
||||||||||||||||||||
− J1(m)cos(ω1 − Ω)t + J2 (m)cos(ω1 ± 2Ω)t + ...))cosω0t = |
|
|||||||||||||||||||
=U |
|
cosω t + |
U0M AМ |
J (m)cos(ω ± ω )t + |
|
|
(4.24) |
|||||||||||||
|
|
|
|
|||||||||||||||||
|
|
0 |
0 |
|
2 |
|
|
0 |
|
|
0 |
|
1 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
+ |
U0M AМ |
J |
1 |
(m)cos(ω |
|
± |
ω |
+ Ω)t − |
U0M AМ |
J |
(m)cos(ω |
± ω − Ω)t + |
||||||||
|
|
|
||||||||||||||||||
|
|
|
2 |
|
0 |
|
|
|
1 |
|
|
2 |
1 |
|
0 |
1 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
+ |
U0M AМ |
J |
2 |
(m)cos(ω ± ω ± 2Ω)t + ... |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|||||||||||||||
|
|
|
2 |
|
|
|
0 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В соответствии с выражением (4.24) спектр ЧМ-АМ-сигнала имеет вид |
||||||||||||||||||||
представленный на рис. 4.14. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
62 |
|
|
|
|
|
` |
|
|
|
|
|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
U0MAM |
J0(m) |
|
U0 |
|
|
U0МАМ |
|
J0(m) |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
U0MAM |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
U0MAM |
` |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Jn(m) |
2 J`n(m) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω
ω0-ω1-nΩ ω0-ω1 ω0-ω1+nΩ ω0 ω0+ω1-nΩ ω0+ω1 ω0+ω1+nΩ
Рис. 4.14. Спектр ЧМ-АМ-сигнала
Как следует из рис. 4.14, полоса частот, занимаемая ЧМ-АМ-сигналом,
равна
∆ωЧM −AM = ω0 |
+ ω1 + nΩ−ω0 |
+ ω1 |
+ nΩ = |
(4.25) |
|
= 2(ω1 + nΩ) ≈ 2(ω1 + mЧМ Ω) = 2(ω1 + ωgн), |
|||||
|
|||||
где mЧМ = ωgн / Ω – индекс частотной модуляции; ωgн – девиация частоты
поднесущей.
Необходимо отметить, что данный вид двукратной модуляции следует применять в том случае, когда требуется обеспечить высокую помехоустойчивость при передаче по узкополосному каналу связи. Тогда помехоустойчивость
обеспечивается ЧМ, а экономия полосы частот – АМ. |
|
4.4.4. ЧМ-ЧМ сигналы. В данном случае |
сначала сообщением |
C(t) =U Ω cos Ωt модулируется по частоте поднесущая, |
а затем ЧМ-сигнал мо- |
дулирует по частоте несущую. Формы сигналов при ЧМ-ЧМ показаны на рис. 4.15.
В общем случае выражение для ЧМ-ЧМ-сигнала можно записать в следующем виде:
UЧМ−ЧМ (t) =U0 cos(ω0t + ∫kUω1 cos(ω1t + mЧМ sinΩt)dt) =
(4.26)
U0 cos(ω0t +ωgн∫cos(ω1t + mЧМ sinΩt)dt) ,
где ωgн = кUω1 – девиация частоты несущей; mЧМ – индекс частотной модуляции поднесущей.
Для построения спектра ЧМ-ЧМ воспользуемся методикой, изложенной при построении спектра АМ-ЧМ-сигнала. Сначала изобразим спектр полезного сообщения (рис. 4.16,а), после чего перенесем его на поднесущую частоту по правилам ЧМ-сигнала (рис. 4.16,б), а затем полученный спектр перенесем на несущую частоту по правилам ЧМ-сигнала (рис. 4.16, в).
63
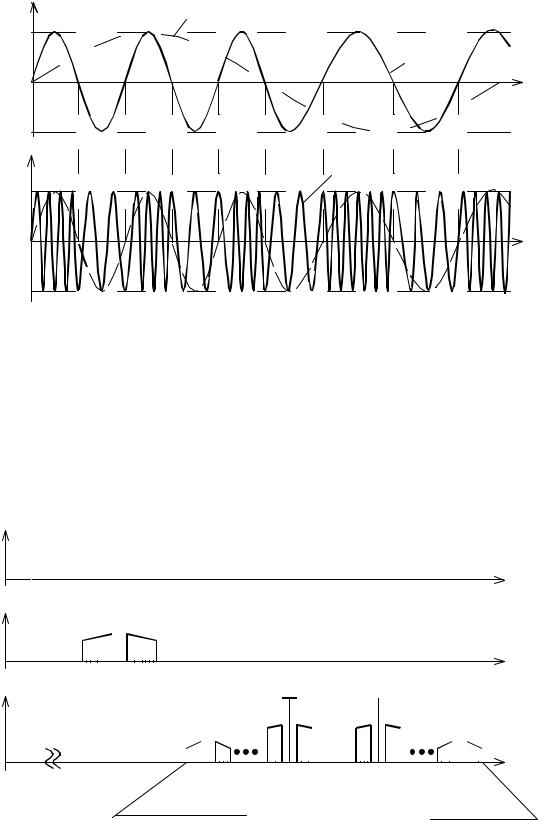
UЧМ(t) |
С(t) |
|
Un(t)
t
UЧМ-ЧМ(t) |
UН(t) |
t
Рис. 4.15. Формы сигнала при ЧМ-ЧМ
Полоса частот, занимаемая ЧМ-ЧМ-сигналом, согласно рис. 4.16, в
∆ω |
− |
= 2(pω + nΩ) 2(M |
ω + m |
Ω) = 2(ω |
н + ωgп ), |
(4.27) |
|
ЧM ЧM |
1 |
ЧМ 1 |
ЧМ |
g |
|
|
|
где MЧМ = ωgн /ω1 – индекс частотной модуляции на второй ступени.
Uс |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω |
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Uчм |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω1−nΩ ω1 |
|
|
|
ω1+nΩ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
Uчм-чм |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω0− |
pω1 ω0−ω1 ω0 ω0+ω1 |
ω0+pω1 |
|||||||||||||||||||||||||||||||||||||
ω0−pω1−nΩ |
ω0+pω1+nΩ |
|
Рис. 4.16. Процесс образования спектра ЧМ-ЧМ-сигнала
Как видно из (4.27) сигнал ЧМ-ЧМ обладает самым широким спектром.
64
