
- •Вводная лекция
- •В.1 Определение, задачи и проблемы
- •В.2 Телемеханические устройства, комплексы и системы
- •В.3 Краткая историческая справка развития телемеханики
- •Часть 1. Сообщения и сигналы
- •СОДЕРЖАНИЕ
- •ВВЕДЕНИЕ
- •1. ОБЩИЕ СВЕДЕНИЯ О СИГНАЛАХ
- •1.1. Основные типы сигналов
- •1.2. Периодические сигналы
- •1.4. Спектр одиночного прямоугольного импульса
- •2. МОДУЛЯЦИЯ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
- •2.1. Амплитудная модуляция
- •2.2. Частотная модуляция (ЧМ)
- •2.3. Фазовая модуляция (ФМ)
- •2.4. Одновременная модуляция по амплитуде и по частоте
- •3. ИМПУЛЬСНАЯ МОДУЛЯЦИЯ
- •3.2. Фазоимпульсная модуляция (ФИМ)
- •3.3. Широтно-импульсная модуляция (ШИМ)
- •4. МАНИПУЛИРОВАННЫЕ СИГНАЛЫ
- •4.1. Амплитудная манипуляция (АМП)
- •4.2. Фазовая манипуляция (ФМП)
- •4.3. Частотная манипуляция (ЧМП)
- •4.4. Двукратная модуляция
- •4.5. Спектры радиоимпульсов
- •5. МОДУЛЯТОРЫ И ДЕМОДУЛЯТОРЫ
- •5.1. Амплитудные модуляторы
- •5.2. Детекторы АМ-сигналов
- •5.3. Модуляторы однополосного сигнала
- •5.4. Детекторы ОАМ-сигнала
- •5.5. Частотные модуляторы
- •5.6. Детекторы ЧМ-сигналов
- •5.7. Фазовые модуляторы
- •5.8. Фазовые детекторы (ФД)
- •5.9. Амплитудно-импульсные модуляторы
- •5.11. Широтно-импульсный модулятор
- •5.12. Демодуляторы ШИМ-сигналов
- •5.13. Фазоимпульсные модуляторы
- •5.14. Детекторы ФИМ-сигналов
- •5.15. Дискретный амплитудный модулятор
- •5.17. Модуляторы ЧМП-сигналов
- •5.19. Модуляторы ФМП-сигналов
- •5.20. Детекторы ФМП-сигнала
- •ЛИТЕРАТУРА
- •Часть 2. Коды и кодирование
- •СОДЕРЖАНИЕ
- •ВВЕДЕНИЕ
- •1. КОДЫ И КОДИРОВАНИЕ
- •1.1. Основные понятия
- •1.2. Цифровые коды
- •1.3. Простые двоичные коды
- •1.4. Оптимальные коды
- •2. КОРРЕКТИРУЮЩИЕ КОДЫ
- •2.1. Основные понятия
- •2.2. Коды с обнаружением ошибок
- •2.3. Коды с обнаружением и исправлением ошибок
- •2.4. Частотные коды
- •3. ТЕХНИЧЕСКИЕ СРЕДСТВА ПРЕОБРАЗОВАНИЯ ДЛЯ НЕПОМЕХОЗАЩИЩЕННЫХ КОДОВ
- •3.2. Дешифратор двоичного кода в десятичный код
- •3.3. Дешифратор двоично–десятичного кода в десятичный
- •3.4. Преобразователи двоичного кода в двоично–десятичный код и обратно
- •3.5. Преобразователь двоичного кода 8–4–2–1 в самодополняющийся двоично–десятичный код 2–4–2–1
- •3.6. Преобразователь самодополняющего двоично–десятичного кода 2–4–2–1 в двоичный код 8–4–2–1
- •3.7. Преобразователь кода Грея в двоичный код и обратно
- •3.8. Технические средства кодирования и декодирования эффективных кодов
- •3.9. Схемы равнозначности кодов
- •4.1. Кодер и декодер кода с защитой на четность
- •4.2. Кодер и декодер кода с постоянным весом
- •4.3. Кодер и декодер кода с двумя проверками на четность
- •4.4. Кодер и декодер кода с повторением
- •4.5. Кодер и декодер кода с числом единиц, кратным трем
- •4.6. Кодер и декодер инверсного кода
- •4.7. Кодер и декодер корреляционного кода
- •4.8. Кодер и декодер кода Бергера
- •4.10. Кодирующее и декодирующее устройство кода Хемминга
- •4.11. Технические средства умножения и деления многочлена на многочлен
- •4.12. Кодер и декодер циклического кода
- •4.13. Кодер и декодер итеративного кода
- •4.14. Кодер и декодер рекуррентного кода
- •5.1. Кодер и декодер кода на перестановки
- •5.2. Кодер и декодер кода на размещения
- •5.3. Кодер и декодер кода на сочетания
- •5.4. Дешифратор одночастотного кода
- •5.5. Кодер и декодер сменно–качественного кода
- •6. КОДЫ ДЛЯ ПЕРЕДАЧИ ЦИФРОВОЙ ИНФОРМАЦИИ ПО ПОСЛЕДОВАТЕЛЬНЫМ КАНАЛАМ СВЯЗИ
- •6.1. Методы кодирования
- •6.2. Шифратор и дешифратор кода Манчестер–2
- •ЗАКЛЮЧЕНИЕ
- •ЛИТЕРАТУРА
- •Часть 3. Линии связи и помехоустойчивость информации
- •СОДЕРЖАНИЕ
- •ВВЕДЕНИЕ
- •1. ЛИНИИ И КАНАЛЫ СВЯЗИ
- •1.1. Понятие о линии и канале связи
- •1.2. Способы разделения каналов
- •1.3. Проводные линии связи
- •1.4. Использование высоковольтных линий электропередачи (ЛЭП) в качестве линий связи
- •1.6. Радиолинии
- •1.7. Оптические линии связи
- •1.9. Структура линий связи
- •1.10. Сети передачи дискретных сообщений
- •1.11. Расчет основных характеристик цифровых линий связи
- •1.12. Расчет волоконно–оптической линии связи
- •2. ПОМЕХИ И ИХ ХАРАКТЕРИСТИКИ
- •2.1. Общие сведения о помехах
- •2.2. Математическое описание помехи
- •2.3. Виды искажений
- •3. ПОМЕХОУСТОЙЧИВОСТЬ ПЕРЕДАЧИ ДИСКРЕТНЫХ СООБЩЕНИЙ
- •3.1. Основные понятия
- •3.2. Помехоустойчивость передачи дискретных элементарных сигналов
- •3.3. Приём с зоной стирания
- •3.4. Помехоустойчивость двоичных неизбыточных кодов
- •3.5. Помехоустойчивость кодов с обнаружением ошибок
- •3.7. Помехоустойчивость систем с дублированием сообщений
- •3.8. Помехоустойчивость систем с обратными каналами связи
- •4. ПОМЕХОУСТОЙЧИВОСТЬ ПЕРЕДАЧИ НЕПРЕРЫВНЫХ СООБЩЕНИЙ
- •4.1. Общие соображения
- •4.2. Помехоустойчивость непрерывных методов модуляции
- •4.3. Помехоустойчивость импульсных методов модуляции
- •4.4. Потенциальная помехоустойчивость сложных видов модуляции
- •5. МЕТОДЫ ПОВЫШЕНИЯ ПОМЕХОУСТОЙЧИВОСТИ
- •5.1. Методы повышения помехоустойчивости передачи дискретных сообщений
- •5.2. Методы повышения помехоустойчивости передачи непрерывных сообщений
- •ЛИТЕРАТУРА
- •ПРИЛОЖЕНИЕ
3.5. Преобразователь двоичного кода 8–4–2–1 в самодополняющийся двоично–десятичный код 2–4–2–1
Представим числа в двоичном коде как y4 y3 y2 y1 , а числа в самодополняющем коде как x4 x3 x2 x1. Тогда разряды xi через yi будут определяться из
выражений:
x1 = y1;
x2 = y4 y3 y2 + y4 y3 y2 + y4 y3 y2 y1;
x3 = y4 y3 y2 + y4 y3 y1 + y4 y3 y2 ;
(3.1)
x4 = y4 y3 y2 + y4 y3 y1 + y4 y3 y2 .
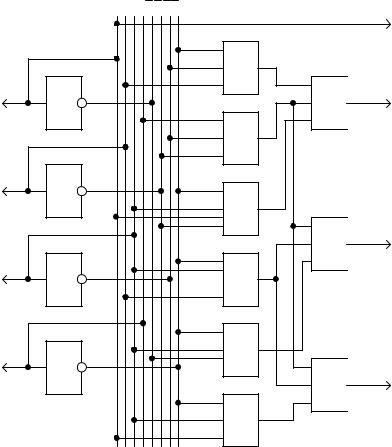
Функциональная электрическая схема преобразователя кода 8–4–2–1 в код 2–4–2–1, построенного по выражению (3.1), приведена на рис. 3.16.
Вход двоичного кода 8-4-2-1
|
|
|
y1y2y3y4y1y2y3y4 |
|
|
|
|
& |
|
y1 |
20 |
1 |
DD5 |
|
DD1 |
& |
|||
|
|
|||
|
|
|
DD6 |
|
y2 |
21 |
1 |
& |
|
DD2 |
||||
|
|
|
||
|
|
|
DD7 |
|
y3 |
22 |
1 |
& |
|
DD3 |
DD8 |
|||
|
|
|||
|
|
1 |
& |
|
y4 |
23 |
DD9 |
||
DD4 |
||||
|
|
|
||
|
|
|
& |
|
|
|
|
DD10 |
|
|
X1 |
1 |
|
|
|
|
|
|
1 |
|
X2 |
2 |
|
|
|
|||
|
|
|
||
DD11 |
|
|
|
|
|
|
|
|
|
1 |
|
X3 |
4 |
1-2-4-2 |
|
||||
|
||||
DD12 |
|
|
кодаВыход |
|
|
|
|
||
|
|
|
|
|
1 |
|
X4 |
2 |
|
|
|
|||
|
|
|||
|
|
|
||
DD13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.16. Преобразователь кода 8-4-2-1 в код 2-4-2-1
86
Табл. 3.9, поясняющая работу схемы, составлена таким образом. В верхних четырех строках записан преобразуемый двоичный код, а в самой нижней
– десятичные числа. Во второй – пятой строках снизу зафиксированы комбинации кода 2–4–2–1, которые образуются на выходах схем DD11…DD13 и X1. В остальных строках таблицы записаны единицы или нули, которые образуются на выходах промежуточных элементов.
Таблица 3.9
Преобразование кода 8–4–2–1 в код 2–4–2–1
|
Входов |
y1(20) |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
|
y2(21) |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
|
|
y3(22) |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
|
|
y4(23) |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
|
|
|
|||||||||||
|
элементов |
DD1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
Н И Я |
DD2 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|
DD3 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
||
DD4 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
||
С О С Т О Я |
Промежуточных |
DD5 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
DD6 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
||
DD7 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
||
DD8 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
||
DD9 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
||
|
DD10 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
|
|
|
|||||||||||
|
Выходов |
x1(1) |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
|
x2(2) |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
|
|
x3(4) |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
|
|
x4(2) |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
|
|
|
|||||||||||
Десятичное число |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
||
3.6. Преобразователь самодополняющего двоично–десятичного кода 2–4–2–1 в двоичный код 8–4–2–1
На основании анализа столбцов 2 и 3 табл. 1.3 и введенных обозначений разрядов в подразделе 3.5, разряды кода 2–4–2–1 связаны с разрядами кода 8– 4–2–1 следующими выражениями:
y1 = x1;
y2 = x4 x3x2 + x4 x3 x2
y3 = x4 x3 x2 x1 + x4 x3 x2 + x3x2 x1; |
|
y4 = x4 x3x2. |
(3.2) |
87
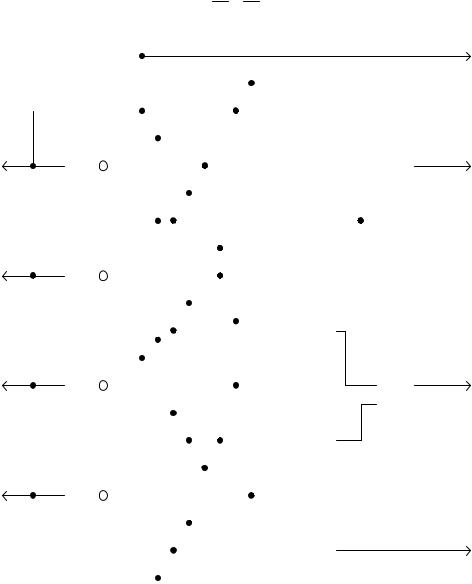
Функциональная электрическая схема преобразователя, построенная на основании выражений (3.2), приведена на рис. 3.17, а принцип работы поясняется табл. 3.10.
Вход двоично-десятичного кода 2-4-2-1
1
X1
2
X2
3
X3
4
X4
X2 X4 X2 X4
|
|
|
X1 X3 |
X1 |
|
X3 |
|
|
|
|
Y1 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
DD5 |
|
|
|
|
|
|
1 |
|
1 |
Y2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
DD1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
DD10 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
DD6 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
DD2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
DD7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
|
1 |
Y3 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
DD3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
DD11 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
DD8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
DD4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
|
|
|
|
Y4 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
DD9 |
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.17. Схема преобразователя кода 2-4-2-1 в код 8-4-2-1
88
Таблица 3.10
|
|
Входов |
x1(1) |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
|
|
x2(2) |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
|
|
|
|
|||||||||||
|
|
|
x3(4) |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
|
|
|
x4(2) |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
|
|
|
DD1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
НЯОТСОСИ Я |
|
Промежуточных элементов |
DD2 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
|
DD3 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
||
|
|
|
|||||||||||
|
|
|
DD4 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
|
|
|
DD5 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|
DD6 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
|
|
|
DD7 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
|
|
DD8 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
|
|
|
DD9 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
|
|
Выходов |
y1(1) |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
|
|
y2(2) |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
|
|
|
|
|||||||||||
|
|
|
y3(4) |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
|
|
|
y4(8) |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
|
Десятичное число |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.7. Преобразователь кода Грея в двоичный код и обратно
Как указано в подразд. 1.3.5, значение каждого последующего разряда двоичного числа находится путем сложения по модулю 2 этого же разряда в коде Грея с предыдущим (1.8), т.е.
i
ai = ∑bi (mod2) ,
i=n
а для определения i–го разряда в коде Грея необходимо сложить по модулю 2 значение преобразуемого разряда двоичного кода со значением предыдущего разряда этого же кода (1.9), т.е.
bi = ai+1 ai .
Оба эти выражения определяют алгоритмы преобразования кода Грея в двоичный код и обратно.
89
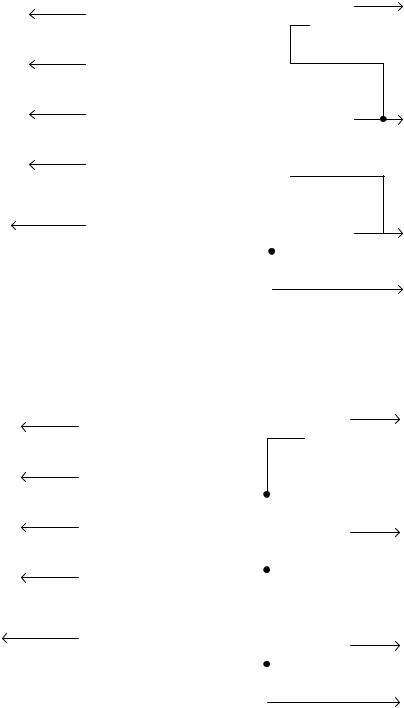
На рис. 3.18 показана функциональная схема преобразователя четырех разрядного кода Грея в четырех разрядный двоичный код, а на рис. 3.19 схема обратного преобразования. Соответствие кода Грея двоичному и наоборот показано в табл. 3.11.
Вход кода Грея
1 |
|
|
|
|
|
|
|
=1 |
||||
D0 |
RG |
1 |
|
|
|
|
|
|||||
b1 |
|
|
|
|
DD2 |
|||||||
|
|
|
|
|||||||||
|
|
|
|
|
|
|||||||
3 |
|
|
|
|
|
|
|
|||||
D1 |
|
|
|
|
|
|
|
|||||
b2 |
|
3 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
D2 |
|
|
|
|
|
=1 |
|||||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
||||||
b3 |
|
|
|
|
|
|
|
|||||
15 |
D3 |
|
7 |
|
|
|
|
DD3 |
||||
|
|
|
|
|
||||||||
b4 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
зап |
V |
DD1 |
15 |
|
|
|
|
=1 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
DD4 |
||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
a1
1
a2 кодадвоичного Выход
2
a3  4
4
a4
8
Рис. 3.18. Преобразователь кода Грея в двоичный
Вход двоичного кода
|
|
1 |
|
|
|
|
|
|
=1 |
b1 |
|
||
|
|
|
RG |
1 |
|
|
|
|
|
||||
a1 |
D0 |
|
|
|
|
1 |
|
||||||
2 |
|
|
|
DD2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||
a2 |
D1 |
|
2 |
|
|
|
|
|
Грея |
||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
D2 |
|
|
|
|
|
=1 |
b2 |
кода |
||
a3 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
3 |
||||
a4 |
8 |
D3 |
|
4 |
|
|
|
DD3 |
|
Выход |
|||
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
зап |
V |
DD1 |
8 |
|
|
|
=1 |
b3 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
7 |
|
|||
|
|
|
|
|
|
|
|
|
DD4 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
b4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.19. Преобразователь двоичного кода в код Грея |
|
||||||||||||
90
Таблица 3.11
Соответствие четырехразрядного кода Грея двоичному коду 8–4–2–1
|
a1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
код |
|
a2 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Двоичный |
|
a3 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a4 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
Вход |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b2 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
Грея |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Выход |
b3 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
Код |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b4 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Десятич- |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
|
ный код |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
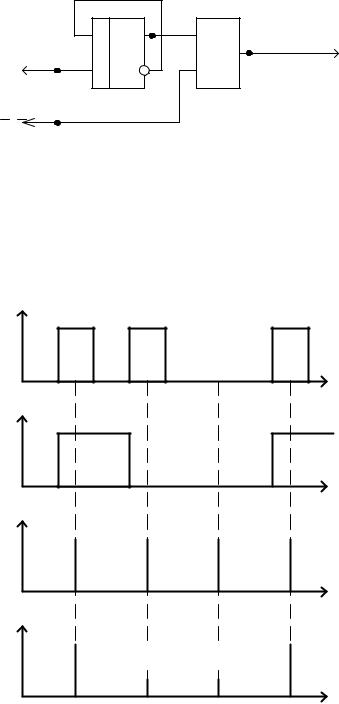
Преобразование последовательного кода Грея в двоичный можно осуществить с помощью преобразователя, схема которого приведена на рис. 3.20. Кодовые комбинации на вход триггера DD1 поступают начиная со старшего разряда. Триггер осуществляет операцию суммирования по модулю 2. Принцип работы наглядно поясняется временными диаграммами, приведенными на рис. 3.21.
91
|
D |
2 |
1001 & |
1001 Выход |
Вход 1 |
|
|||
|
DD2 4 |
|||
C DD1 |
|
|||
1101 |
|
|||

 такт
такт
3
Рис. 3.20. Преобразователь последовательного кода Грея в двоичный
1
1 |
1 |
0 |
1 |
|
|
|
t |
2
t
3
t
4
1 |
|
0 |
|
0 |
|
1 |
|
|
|
t
Рис. 3.21. Временные диаграммы работы преобразователя кода Грея в двоичный
92
