39.Основи тривимірної графіки. Перетворення тривимірних координат. Повороти

В основі будь-якого методу побудови моделей у просторі лежить координатний метод. Положення точки в просторі визначається трьома координатами – x,y,z.

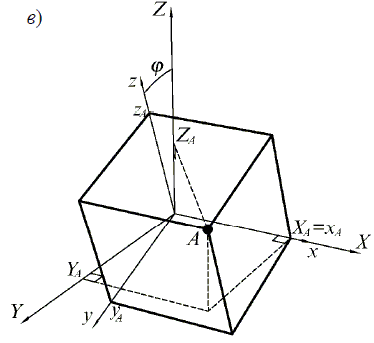
Положення об’єкта в просторі може бути задано координатами деякої базової точки, що є центром його власної системи координат, і трьома кутами повороту цієї системи координат щодо кожної з осей загальної системи координат.

Перетворення координат у просторі включає масштабування, поворот і зсув.

У загальному виді афінні перетворення в просторі можуть бути представлені системою рівнянь:

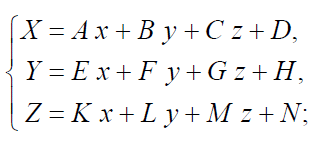Або в матричному виді:

Де x,y,z – координати точки в локальній системі координат об’єкта

X,Y,Z– координати цієї ж точки в глобальній системі координат

A,B…N- константи перетворення.

-навколо осі X на кут φ:

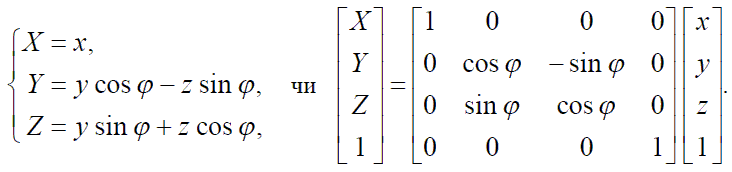
-навколо осі Y на кут ψ:

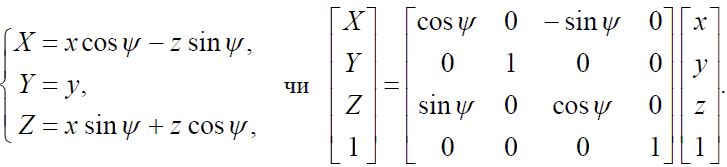
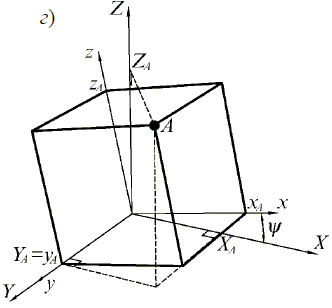
-навколо осі Z на кут γ:

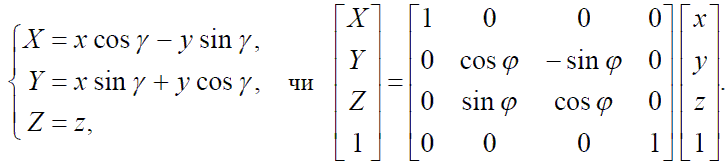
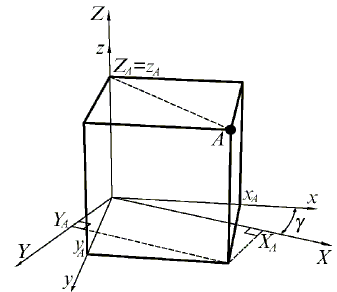
Як можна бачити, при повороті навколо деякої осі глобальної системи координат координата точки по цій осі залишається незмінною, інші дві координати перетворяться аналогічно повороту на площині.

Послідовно виконуючи операції масштабування, зсуву і поворотів навколо осей X,Y,Z можна розташувати деякий об’єкт у довільному положенні в деякій області простору.

40. Поняття проекції та світових координат

41. Екранні координати

Проекція об’єкта – це зображення, отримане як результат перетинання поверхні проектування пучком паралельних або збіжних променів, що проектують, які йдуть від цього об’єкта.

У комп’ютерній графіці найбільш поширені паралельна і центральна проекції. Паралельна проекція створюється пучком променів, паралельних один одному. Центральна проекція, яку також називають перспективною, виходить, що коли промені, що проектують виходять з однієї точки простору. Останній вид проекції дозволяє створити зображення, що ближче до тієї картинки, яку сприймає наше око, а тому виглядає реалістичніше.

При відображенні просторових об’єктів на екрані або листі паперу за допомогою принтера, необхідно знати координати проекцій точок об’єкта на екран або лист. Звичайно використовують дві системи координат – світову й екранну.

Світові координатиописують дійсне положення об’єктів у просторі. У більшості випадків це тривимірна прямокутна система координат.

Екранні координати– це система координат пристрою відображення, яке здійснює виведення зображень об’єктів у заданій проекції.

Для одержання зображення тривимірного об’єкта на пристрої відображення необхідно знати перетворення координат зі світових в екранні.

42. Аналітична модель опису тривимірних поверхонь

Аналітична модель — опис поверхні математичними формулами.

Поверхня може бути задана у вигляді функції двох аргументів:

z =f (x,y) або у виглядірівняння:F (x,y,z) = 0

але найчастіше зустрічається параметрична форма опису поверхні:

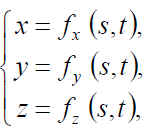деfx,fy,fz – функції, що визначають форму поверхні;s іt – параметри цих

функцій. Параметрична форма дозволяє простіше описувати складні поверхні, у

тому числі замкнені та поверхні, що відповідають неоднозначним функціям.

Наприклад, сферу можна описати як функцію двох аргументів, рівнянням і в

параметричній формі в такий спосіб:

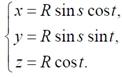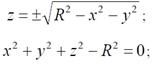,Існують кілька варіацій аналітичного методу опису поверхонь і тіл, які використовують у різних областях моделювання. У САПР для створення

моделей тіл типу деталей машин, що характеризуються відносно простимиформами, застосовується твердотілове моделювання. Відомі два методи твердотілового моделювання:метод геометричних примітивів ікінематичнийметод.Метод геометричних примітивів полягає у створенні моделі об’єкта з набору стандартних об’ємних фігур, які досить просто описуються аналітично. Звичайно це прямокутний паралелепіпед, циліндр, конус, сфера, тороїд. Модель об’єкта створюється шляхом виконання топологічних операцій над примітивами: додаванням, відніманням, перетинанням, усіканням площиною.Кінематичний метод дозволяє описати поверхні як слід у просторі від руху деякої лінії (утворюючої) по заданій траєкторії. Звичайно використовують рух уздовж відрізка прямої (видавлювання),обертання, а також рух уздовж

довільної траєкторії.Твердотілові моделі подають інформацію не тільки про поверхню об’єкта, але і про його обсяг, масу. Крім того, твердотілові аналітичні моделі дозволяють виконуватитопологічні операції над об’єктами: одержувати розрізи, перетини, складати і віднімати об’єкти. Наприклад, щоб одержати модель пресформи, достатньо з її заготовки відняти модель готової деталі. Твердотілові моделі дають можливість знаходити області взаємного перетинання об’єктів, наприклад, для аналізу помилок взаємного розташування деталей у проектованому вузлі. У ціломуаналітичні моделі найбільш придатні для операцій аналізу поверхонь, дозволяють досить просто розрахувати координати вектора нормалі до кожної точки поверхні. Недоліки аналітичних моделей — складність формул опису, необхідність виконання великих обсягів обчислень для побудови реалістичних зображень поверхонь. Тому в інтерактивній 3D-анімації (іграх, симуляторах) аналітичні моделі поверхонь не використовуються. Основна область застосування аналітичних моделей САПР і високоякісна 3D-анімація (художні фільм)