2.10.2. Центральний не пружний удар двох куль.

При цьому ударі тіла деформуються в точці дотику і потім рухаються з однаковою швидкістю U. Рівняння збереження імпульсу має вигляд

,

і звідси

. (9)

Робота А, витрачена на деформацію, дорівнює різниці енергій шарів до удару і після удару

,

і після підстановки значення з (9) одержимо

.

2.10.3. Частково пружний удар, коефіцієнт відновлення.

При частково пружному ударі не повністю відновлюється відносна швидкість системи. Можна покласти, що

,

де  коефіцієнт відновлення швидкості. З рівняння збереження імпульсу тепер можна знайти швидкості тіл після удару

, (10)

. (11)

Рівняння збереження енергії тепер запишеться як

. (12)

П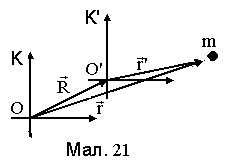ідставляючи (10-11) у (12) одержимо величину роботи А на не пружну деформацію тіл

. (13)

Робота А чисельно дорівнює втраті тілами кінетичної енергії.

Зауважимо, що при k=1 удар буде абсолютно пружним, при k=0  не пружним і при 0 k 1  частково пружним.

2.11. Принцип відносності Галілея

2.11.1. Механічний принцип відносності Галілея полягає у тому, що усі механічні явища в різних інерційних системах протікають за однаковими для цих явищ законами за змістом і формою.

Перетворення координат Галілея: час у різних інерційних системах протікає однаково t=t', а координати при переході з нерухомої системи відліку до рухомої (див. мал. 21) перетворюються лінійно:

,

де швидкість рухомої системи відносно нерухомої.

З цього виразу можна одержати рівняння перетворення швидкостей

.

В цьому виразі  абсолютна швидкість, тобто швидкість тіла в нерухомій системі відліку,  швидкість тіла в рухомій системі відліку, яку називають відносною. Такі ж вирази можна одержати і для прискорень , .

2.11.2. Рівняння другого закону Ньютона в нерухомій системі відліку має вигляд m, в рухомій  , де сила інерції.

У випадку, коли система K' інерційна, тобто , то,і рівняння другого закону Ньютона зберігають свій вигляд як у нерухомій так і у рухомій інерційній системі відліку. Це і пояснює принцип відносності Галілея.

2.12.Динаміка обертового руху

2.12.1. Момент сили

В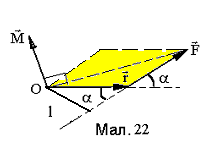обертовому русі замість силивикористовується момент сили, а замість імпульсувживається момент імпульсу. Момент сили визначається так, щоб вектори кутової швидкості та кутового прискорення, які виникають внаслідок його дії, збігалися з напрямком. Таким чином зазначеній умові відповідає момент сили, який дорівнює векторному добуткові радіус-вектораточки прикладання сили відносно початку відліку О (див. Мал. 22) й вектора сили

. (1)

У виразі (1) l  плече сили F. Чисельно момент сили дорівнює площі закрашеного паралелограма, побудованого на векторах , причому плече сили дорівнює висоті паралелограма, опущеної на основуF.

Дві рівні за величиною сили , що лежать в одній площині і діють на тіло в протилежних напрямках,називаються парою сил. Їх моменти сил відносно точки О будуть , а результуючий моментза величиною

,

де плече сили F₁, плече силиF₂, плече пари сил, а F=F₁=F₂.

2.12.2. Момент імпульсу

Момент імпульсу тіла визначається як вектор, що дорівнює векторному добуткові радіус-вектора (див. Мал. 15) положення тіла й вектора імпульсу тіла

. (2)

Розглянемо момент імпульсу докладніше, прийнявши до уваги визначення імпульсу та кутових і лінійних характеристик обертового руху. Н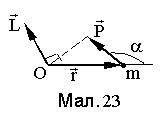ехай точкове тіло обертається по колу з радіусом-вектором положення тіла  лінійній швидкості . Вираз (1) у цьому випадку можна послідовно перетворити у вигляд:

(3)

,

де

, (4)

момент інерції тіла.

де J  величина моменту інерції тіла.

В (3) ми використали відому формулу для подвійного векторного добутку (див. Математичний додаток)

.

Таким чином момент імпульсу (3) дорівнює добуткові моменту інерції тіла J на його кутову швидкість , які є аналогами маси тіла m та його швидкості у поступальному русі.