2.2.3. Третій закон Ньютона.

Дія одного точкового тіла на інше носить характер взаємодії. Сили взаємодії рівні за величиною, лежать на одній прямій, що з'єднує тіла і протилежні за напрямком, тобто, якщо на перше тіло діє сила , то на друге тіло буде діяти сила.

Розглянемо приклади на застосування другого закону Ньютона.

При визначеній силі , що діє на тіло та заданих початкових умовах для швидкості

та радіус-вектора положення тіла

,

можна визначити місцеположення тіла для довільного моменту часу. Дійсно, по заданій силі

та масі тіла m, знаходимо прискорення

.

Далі з визначення швидкості знайдемо її компоненти

через інтегрування компонент прискорення

.

На останньому кроці за рівнянням знайдемо компоненти радіус-вектора положення тіла шляхом інтегрування компонент швидкості

.

2.3. Імпульс та закон збереження імпульсу

2.3.1. Імпульс сили та імпульс тіла

Імпульс сили визначається як добуток сили на час її дії на тіло:

.

Імпульс тіла (кількість руху) є добуток маси тіла на його швидкість

.

Одиницею вимірювання величини імпульсу сили є , а імпульсу тіла.

Рівняння другого закону Ньютона можна записати через імпульс таким чином

_.

З цього рівняння слідує що , тобто приріст імпульс тіла дорівнює імпульсу сили, що діє на нього.

Наведена форма запису другого закону Ньютона через імпульс є інваріантною і може використовуватися як у класичній, так і в релятивістській механіці.

2.3.2. Закон збереження імпульсу

Замкнена механічна система  це система тіл, на які не діють зовнішні сили.

Закон збереження імпульсу  імпульс замкненої системи зберігається за величиною й напрямком. Він випливає з третього закону Ньютона, який можна сформулювати ще й так: дія і-ої матеріальної точки на j-ту точку носить характер взаємодії; сили взаємодії чисельно рівні, їх вектори лежать на одній прямій і протилежні за напрямком . Нехай система, наприклад, складається з трьох тіл. Запишемо рівняння руху для кожного з них:

.

В цьому виразі  сила, що діє з боку j-того тіла на i-те тіло,  зовнішня сила, що діє на і-те тіло,  імпульс і-того тіла. Додамо ліві та праві частини записаних рівнянь

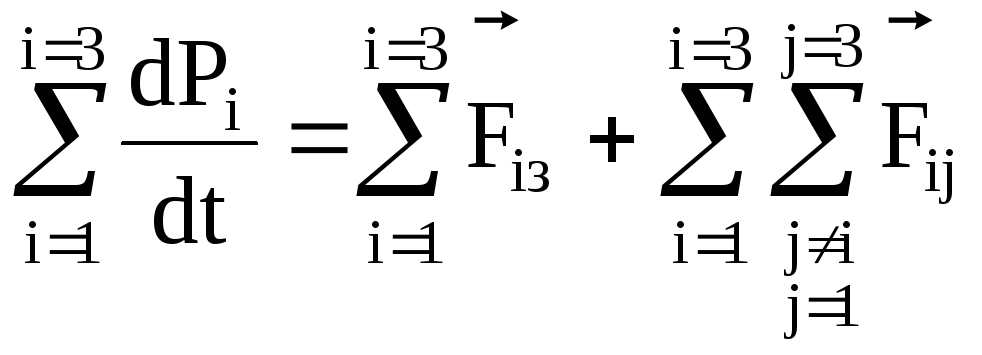
Ліворуч будемо мати суму похідних:

,

яка дорівнює похідній від суми імпульсів

,

де  імпульс системи тіл. В сумі праворуч будуть доданки та сума, що має попарні нульові доданки. Таким чином, праворуч залишиться:

,

де  сума зовнішніх сил, прикладених до різних тіл. Сила не є рівнодійною, її ще називають генеральною. В результаті маємо . Якщо система замкнена, то

.

Закон збереження імпульсу означає, що внутрішні сили взаємодії між тілами замкненої системи не змінюють імпульс системи. Нехай у моменти чаусt₁ та час t₂ відбулися співударяння тіл замкненої системи. За законом збереження імпульсу

.

2.4. Центр мас (інерції)

Центром мас (центр інерції) системи з N тіл з масами є уявна матеріальна точка в просторі з масою М, що дорівнює масі системи тіл. Радіус-вектор центра масзадається рівнянням:

, .

Швидкість центра мас можна представити через імпульс системи тіл таким чином

.

Імпульс центра мас дорівнює імпульсу системи тіл. Оскільки імпульс замкненої системи тіл зберігається, то й швидкість центра мас такої системи при будь-якій взаємодії між її тілами також зберігається .

Якщо в деякий момент часу центр мас не рухався , то при відсутності зовнішніх сил він не змінить свого положення при будь-якій взаємодії між тілами. Дійсно,і .

У випадку незамкненої системи тіл, коли векторна сума зовнішніх сил, що діють на тіла системи дорівнює , рівняння руху центра мас запишеться у вигляді

.

З одержаного рівняння випливає теорема про рух центра мас: центр мас системи тіл рухається як матеріальна точка, маса якої дорівнює масі тіл системи, а прикладена сила – векторній сумі зовнішніх сил, прикладених до кожного з тіл системи.

Якщо система тіл знаходиться у полі сил тяжіння, то центром тяжіння є точка прикладання рівнодійної сил тяжіння всіх частинок.