Розв’язання:

Знайдемо t_Y користуючись додатком №2:

Користуючись таблицею значень t_Y ( додаток 2 ) за n=50 і у=0,95 знаходимо t_Y =2,009.

Знайдемо довірчі інтервали для вибірки Х:

(3.2)

Підставляємо всі значення в формулу і отримуємо:

-0,2197 < a < 1,4161

Отже, з надійністю 0,95 невідомий параметр a знаходиться в довірчому інтервалі -0,2197 < a < 1,4161.

Знайдемо довірчі інтервали для вибірки Y:

(3.3)

Підставляємо всі значення в формулу

-0,3060 < a < 0.0884

Отже, з надійністю 0,95 невідомий параметр a знаходиться в довірчому інтервалі -0,3060 < a < 0.0884.

Висновок: Ми оцінили невідомі математичні сподівання М[Х] і M[У] генеральних сукупностей Х і У за допомогою довірчого інтервалу з надійністю 0,95. Для вибірки Х з надійністю 0,95 невідомий параметр a знаходиться в довірчому інтервалі -0,2197 < a < 1,4161. Для вибірки Y з надійністю 0,95 невідомий параметр a знаходиться в довірчому інтервалі -0,3060 < a < 0.0884.

4._Перевірка гіпотези про рівність дисперсій генеральних сукупностей для вибірок X та y.

Запропонуємо просту гіпотезу про рівність дисперсій генеральних сукупностей H₀: D(X) = D(Y) при конкуруючій гіпотезі H₁: D(X) ≠ D(Y). Перевіримо запропоновані гіпотези при рівні значущості α = 0,1.

Знайдемо значення критерію, що спостерігається за формулою

(4.1)

де s²_б – більша виправлена дисперсія, s²_м – менша виправлена дисперсія.

Ми маємо великі вибірки (n₁ = n₂ = 50 > 30). Отже за виправлені вибіркові дисперсії можна взяти вибіркові дисперсії, які ми знайшли в пункті 2.

Отже, маючи вибіркові дисперсії двох вибірок можна стверджувати

s²_б ≈ D_в(X) =1,2524 (4.2)

s²_м ≈ D_в(Y) =0,4821 (4.3)

Підставимо значення (4.2) та (4.3) в формулу (4.1), отримаємо

F_емп= 2,5978

За умовою задачі, конкуруюча гіпотеза має вигляд H₁: D(X) ≠ D(Y), тому критична область – двостороння.

По таблиці Фішера-Снедекора, по рівню значущості, що в двічі менший за заданий, тобто при α/2 = 0,1/2 = 0,05, та кількістю степенів свободи k₁ =49

k₂ =49 знаходимо критичну точку F_кр(0,05; 49, 49) = 1,96

Так як спостережений критерій більший за критичний F_емп > F_кр (1,66 < 2,5978), то немає підстави відхилити запропоновану гіпотезу, тобто нульова гіпотеза приймається.

Висновок: Результати показують, що вибіркові виправлені дисперсії двох вибірок відрізняються суттєво. Враховуючи, що вибіркові виправлені дисперсії є незміщеними оцінками генеральних дисперсій, то це ж стосується і генеральних дисперсій.

5. Побудова нормальних кривих за емпіричними даними.

Нормальна крива – це графік густини нормального розподілу (крива Гауса). Рівняння густини нормального розподілу:

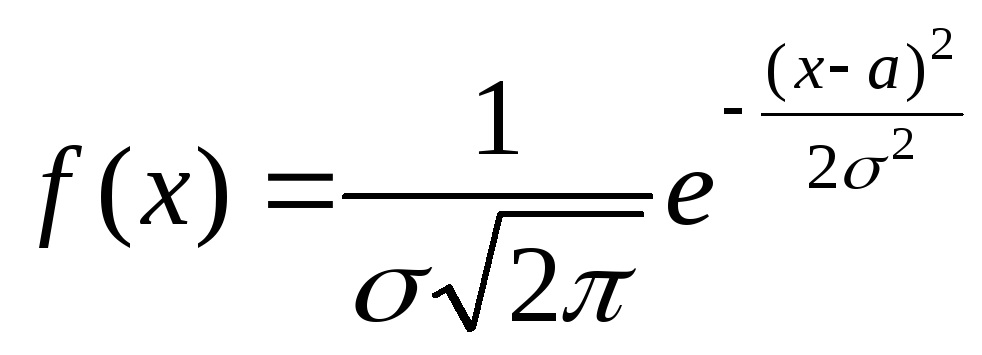(5.1)

де ­σ – середнє квадратичне відхилення, а – математичне сподівання.

5.1 Знаходження вибіркової середньої та середнього квадратичного відхилення методом добутків.

Вибіркові дисперсії вибірок Х та Y вже знайдені методом добутків раніше. За формулою знайдемо середні квадратичні відхилення вибірок.

(5.1.1)

Отримаємо:

σ_Xв = 1,1078, σ_Yв = 0,6873 (5.1.2)

Використаємо обраховані раніше умовні моменти першого порядку (див. (2.15) та (2.16)). Знаючи їх можна легко обчислити вибіркові середні за формулою:

(5.1.3)

Отримаємо: = 0,0982 = -0,1088 (5.1.4)