2.Знаходження оцінок математичних сподівань і дисперсій генеральних сукупностей

Складемо функцію правдоподібності:[1, ст.170]

L = f (x₁; Θ₁, Θ₂) ∙ f (x₂; Θ₁, Θ₂) … f (x_n; Θ₁, Θ₂) (2.1)

За умовою задачі Θ₁ = a(математичному сподіванню), Θ₂ = D_в (вибірковій дисперсії).Для спрощення обчислень D_в замінимо на σ²(виправлену вибіркову дисперсію). У даному випадку випадкові величини неперервні і розподілені за нормальним розподілом, густина якого визначається формулою(2.2)

[2, ст.127]:

, (2.2)

де - математичне сподівання,- середнє квадратичне відхилення.

Отже

L = f (x_i ; Θ₁, Θ₂) = f (x_i ; a, σ²) = 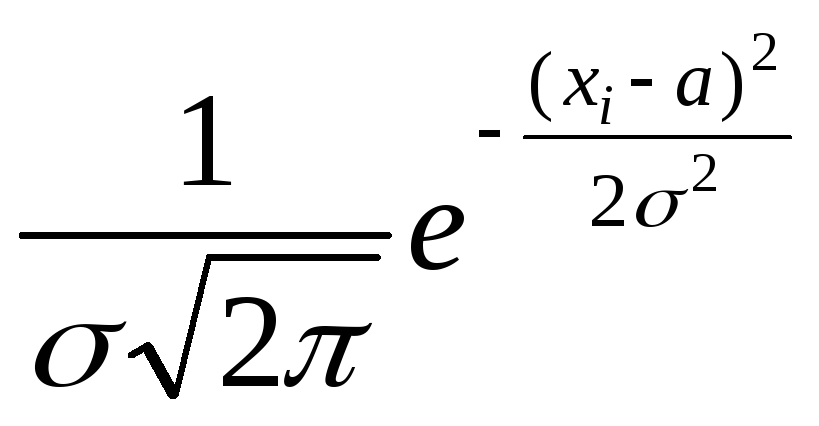(2.3)

Знайдемо максимум функції L. Для цього можна використати функцію ln(L), яка матиме такий же максимум. Тож знайдемо логарифмічну функцію правдоподібності:

ln(L) = Σ ln(f (x_і ; a, σ²)) ==

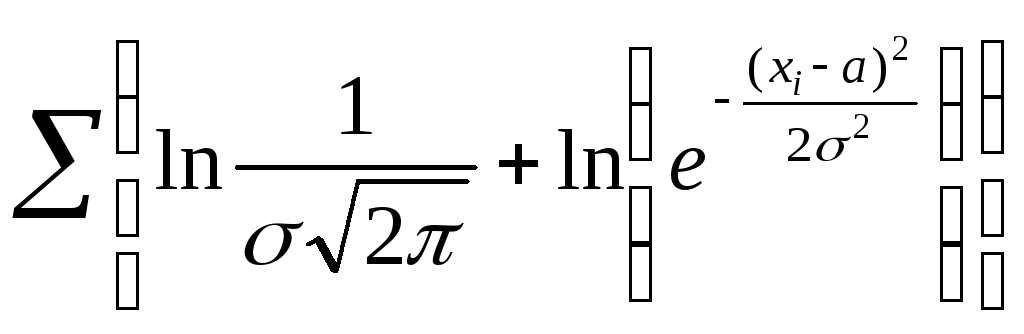== –nln() – =

(2.4)

Знайдемо першу похідну рівняння (2.4) по а:

=

= (Σx_i – na) (2.5)

Знайдемо першу похідну рівняння (2.4) по σ²:

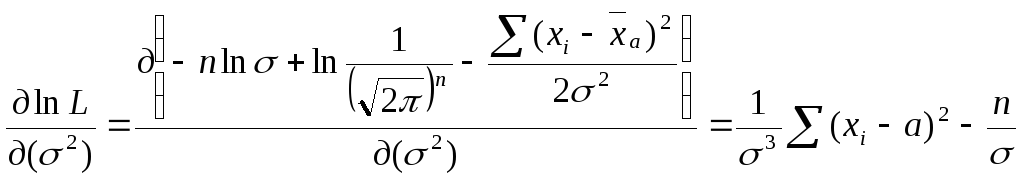(2.6)

Знайдемо критичні точки, для чого прирівняємо часткові похідні (2.5) та (2.6) до нуля і отримаємо систему рівнянь:

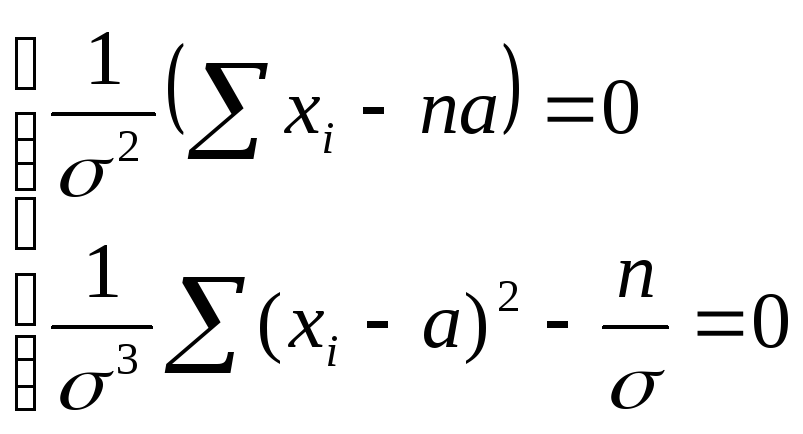(2.7)

Розв’яжемо систему рівнянь (2.7) відносно a. Отримаємо:

(2.8)

Легко бачити, що при а = x_в друга похідна від’ємна, отже ця точка є точкою максимуму і значить в якості оцінки найбільшої правдоподібності треба взяти середнє вибіркове: .

Розв’яжемо систему рівнянь (2.4) відносно σ². Отримаємо:

(Σx_i – a) = n , (2.9)

Підставимо в вираз замість а – середнє вибіркове (див. (2.8)).

(2.10)

Легко бачити, що при такому значенні вибіркової дисперсії друга похідна від’ємна, отже ця точка є точкою максимуму і значить в якості оцінки найбільшої правдоподібності треба взяти наступний вираз:

D_в^* = (2.11)

Вибіркове середнє і вибіркову дисперсію доцільно обчислювати методом добутків, який дає зручний спосіб знаходження умовних моментів різного порядку з рівновіддаленими варіантами.

Обрахуємо вибіркові дисперсії для вибірок X та Y методом добутків. Для цього використаємо рівновіддалені частоти, які ми знайшли в пункті

Вибіркова сукупність Х:

Так як ми вже знайшли певні значення в першому пункті то використаємо їх для розв’язку цього завдання. Створимо таблицю, що необхідна для розв’язання поставлених завдання методом добутків.

Крок нам уже відомий, тому його шукати не будемо.

Вибираємо помилковий нуль. Візьмемо за нього варіанту, якій відповідає найбільша по модулю частота серед варіант, що знаходяться приблизно в середині відсортованого списку варіант. За таким принципом вибираємо 0,941.

C=-0,941

Тепер у таблиці, наведеній нижче. заповнюємо стовпець №3 за таким принципом: напроти варіанти, яка рівна умовному нулю, ставимо 0. Тепер в клітинки над 0 пишемо-1, -2, -3…, а під – 1, 2, 3… Дане випливає якщо для кожного окремого набору значень визначати за формулою:

(2.12)

Заповнюємо всі стовбці таблиці

Таблиця №3

xi	ni	ui	niui	niui2	ni(ui+1)2
-3,001	1	-4	-4	16	9
-1,542	5	-3	-15	45	20
-0,690	12	-2	-24	48	12
0,070	12	-1	-12	12	0
0,941	16	0	0	0	16
1,594	2	1	2	2	8
2,957	2	2	4	8	18
	50		-49	131	83

Перевіримо, чи правильно ми виконали обчислення за формулою:

Після підстановки всіх значень ми отримали певний результат, а точніше 83. Він співпадає з елементом в нижньому рядку останнього стовпчика. Це означає, що обчислення виконані правильно.

Повернемось до головного завдання - знаходження середнього вибіркового і середньої дисперсії.

(2.13)

(2.14)

Для використання даних формул нам не відомими залишається та .

Обрахуємо їх значення за формулами:

(2.15)

(2.16)

Використаємо дані формули і знайдемо невідомі нам елементи.

Підставимо отримані значення і знайдемо ,

Вибіркова сукупність Y:

Так як ми вже знайшли певні значення в пункті один використаємо їх для розв’язку цього завдання. Створимо таблицю, що необхідна для розв’язання поставлених завдання методом добутків.

Крок нам уже відомий, тому його шукати не будемо.

Вибираємо помилковий нуль. Беремо за нього варіанту, якій відповідає найбільша по модулю частота серед варіант, що знаходяться приблизно в середині відсортованого списку варіант. За таким принципом вибираємо 0,3424.

C=0,3424

Тепер у таблиці, наведеній нижче. заповнюємо стовпець №3 за таким принципом: напроти варіанти, яка рівна умовному нулю, ставимо 0. Тепер в клітинки над 0 пишемо-1, -2, -3…, а під – 1, 2, 3… Дане випливає якщо для кожного окремого набору значень визначати за формулою 2.12

Заповнюємо всі стовбці таблиці

Таблиця №4

yi	ni	ui	niui	niui2	ni(ui+1)2
-1,502	2	-4	-8	32	18
-1,0225	8	-3	-24	72	32
-0,4974	9	-2	-18	36	9
-0,1178	9	-1	-9	9	0
0,3424	17	0	0	0	17
1,041	1	1	1	1	4
1,2732	4	2	8	16	36
	50		-50	166	116

Перевіримо, чи правильно ми виконали обчислення за формулою:

Після підстановки всіх значень ми отримали певний результат, а точніше 321. Він співпадає з елементом в нижньому рядку останнього стобчика. Це означає, що обчислення виконані правильно.

Повернемось до головного завдання - знаходження середнього вибіркового і середньої дисперсії.

Використаємо формули 2.15 та 2.16 і знайдемо невідомі нам елементи:

Підставимо отримані значення і знайдемо ,