Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Донбасская национальная академия строительства и архитектуры

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

конспекты / 1234

.pdf

Скачиваний:

Добавлен:

21.02.2016

Размер:

1.55 Mб

Скачать

☆

1 / 101 2 3 4 5 6 7 8 9 10 > Следующая >>>

МІНІСТЕРСТВО ОСВІТИ, НАУКИ, МОЛОДІ І СПОРТУ УКРАЇНИ

ДОНБАСЬКА НАЦІОНАЛЬНА АКАДЕМІЯ БУДІВНИЦТВА І АРХІТЕКТУРИ

КАФЕДРА «МІСТОБУДУВАННЯ ТА ІНЖЕНЕРНА ГРАФІКА»

КОНСПЕКТ ЛЕКЦІЙ З ДИСЦИПЛІНИ «ІНЖЕНЕРНА ГРАФІКА»

(розділ «Нарисна геометрія») для студентів будівельних

спеціальностей освітньо-кваліфікаційного рівня Бакалавр денної та заочної форми навчання

Склали: БАЛЮБА І.Г. КУЗНЕЦОВ С.Г. ГОРЯГІН Б.Ф. МАЛЮТІНА Т.П. ДАВИДЕНКО І.П.

Затверджено на засіданні	Затверджено на засіданні кафедри
науково-методичної ради,	містобудування та інженерної графіки,
протокол №11 від 19.12.2011	протокол №5 від 01.12.2011

Макіївка - 2012

	2
ЗМІСТ
	стор.
ВСТУП. МЕТА ТА ЗАДАЧІ КУРСУ	6
РОЗДІЛ 1. ТОЧКА, ПРЯМА, ПЛОЩИНА	6
1.1. Комплексне креслення точки і прямої	6
1.1.1. Координати і проекції точок. Епюр (креслення) Г. Монжа	6
1.1.2. Епюр відрізка прямої, його натуральна величина та кути нахилу прямої до
площин проекцій (спосіб прямокутного трикутника)	9
1.1.3. Сліди прямої на площинах проекцій	10
1.1.4. Прямі окремого положення відносно площин проекцій	11
1.2. Взаємне положення прямих. Площина	12
1.2.1. Взаємне положення прямих	12
1.2.2. Проекції кута. Проекції прямого кута	13
1.2.3. Спосіб конкуруючих точок для визначення видимості	13
1.2.4. Завдання площини. Різні способи завдання площини	14
1.2.5. Головні лінії площини	15
1.2.6. Площини окремого положення	17
1.3. Взаємне положення прямої та площини і двох площин	20
1.3.1. Паралельність прямої і площини. Паралельність двох площин	20
1.3.2. Перпендикулярність прямої і площини. Перпендикулярність двох площин	21
1.3.3. Перетин прямої з площиною. Перетин двох непрозорих площин	22
1.3.4. Спосіб площин посередників при визначенні лінії перетину двох площин	24
1.3.5. Матеріали для підготовки до контрольної роботи № 1	24
РОЗДІЛ 2. СПОСОБИ ПЕРЕТВОРЕННЯ КОМПЛЕКСНОГО КРЕСЛЕННЯ	28
2.1. Перетворення проекцій та його значення в нарисній геометрії. Чотири основні
задачі перетворення проекцій	28
2.2. Плоскопаралельне переміщення (скорочено ППП) – один із способів
перетворення проекцій. Розв’язання чотирьох основних задач способом ППП	29
2.3. Обертання навколо осі перпендикулярної площині проекцій – окремий
випадок ППП	31
2.4. Спосіб заміни площин проекцій. Розв’язання основних задач способом ЗПП	32
2.5. Обертання навколо лінії рівня. Спосіб суміщення	34
2.6. Матеріали для підготовки до контрольної роботи № 1	35

	3
РОЗДІЛ 3. БАГАТОГРАННИКИ ТА КРИВІ ПОВЕРХНІ	37
3.1. Перетин граних тіл площиною. Спосіб ребер та спосіб граней при побудові
перетину граних тіл площиною	37
3.2. Побудова розгорток поверхонь	39
3.2.1. Спосіб трикутників	39
3.2.2. Спосіб розкатки	40
3.2.3. Спосіб нормального перерізу	40
3.3. Криві лінії та поверхні	42
3.3.1. Кінематичний принцип утворення кривих ліній та поверхонь	42
3.3.2. Класифікація поверхонь	42
3.3.3. Визначник поверхні. Лінія і точка на поверхні	42
3.3.4. Конічні перерізи	43
3.3.5. Перетин прямої та поверхні – основні принципи	43
3.4. Перетин прямої і поверхні. Алгоритм побудови точок входу та виходу на
поверхнях	45
3.4.1. Перетин прямої з граними поверхнями	45
3.4.2. Перетин прямої з конусом	46
3.4.3. Перетин прямої з похилим циліндром	46
3.4.4. Перетин прямої зі сферою	47
3.5. Взаємний перетин поверхонь. Загальний алгоритм побудови лінії перетину
поверхонь. Способи побудови лінії перетину поверхонь	48
3.5.1. Способи площин-посередників при побудові лінії перетину двох
поверхонь	49
3.5.1а. Спосіб горизонтальних січних площин	49
3.5.1б. Спосіб фронтальних січних площин	51
3.5.1в. Спосіб проекціюючих площин	52
3.5.2. Спосіб сфер при побудові лінії перетину поверхонь обертання	53
3.5.2а. Співвісні поверхні обертання і їх лінії перетину	53
3.5.2б. Перетин поверхонь обертання і сфери з центром на осі обертання	53
3.5.2в. Спосіб концентричних і ексцентричних сфер при побудові лінії перетину
поверхонь обертання	54

	4
РОЗДІЛ 4. ОСНОВИ ОБЧИСЛЮВАЛЬНОЇ ГЕОМЕТРІЇ	58
4.1.Поділ відрізка в заданому співвідношенню	58
4.2. Обчислення точки по заданому відношенню. Рівняння прямої	58
4.3. Рівняння прямої лінії, відрізка, променя в стандартній та природній
параметризаціях	59
4.4. Побудова четвертої вершини паралелограма по трьом заданим.
Рівняння площини	60
4.5. Точкове рівняння площини і простору в стандартній та природній
параметризаціях	61
4.6. Обчислення точки перетину прямої із площиною	63
4.7. Метрика точкового числення	64
4.7.1. Метричний оператор трьох точок. Довжина відрізка прямої. Кут між прямими	64
4.7.2. Основа перпендикуляра, опущеного з точки на пряму	66
4.7.3. Точка виходу з площини та її геометрична інтерпретація. Точка виходу з
площини на відстань d	66
4.7.4. Площа трикутника, розташованого в площині загального положення	67
4.7.5. Визначення вершини піраміди по заданій основі і висоті	67
4.8. Побудова вершини трикутної піраміди по заданій основі, висота якої
проекціюється в центроїд основи	68
4.8.1. Вступ	68
4.8.2. Базові поняття	69
4.8.3. Векторний добуток векторів та їх інтерпретація в точковому численні	73
РОЗДІЛ 5. ТЕОРЕТИЧНІ ОСНОВИ АКСОНОМЕТРІЇ	75
5.1. Основні поняття аксонометрії	75
5.2. Основні теореми аксонометрії	76
5.3. Види аксонометрії	77
5.4. Приведені показники спотворення. Стандартні види аксонометрії	77
5.4.1. Прямокутні проекції	78
5.4.2. Косокутні проекції	79
5.5. Координатний спосіб побудови аксонометрії	79
РОЗДІЛ 6. ПРОЕКЦІЇ З ЧИСЛОВИМИ ПОЗНАЧКАМИ	81
6.1. Основні поняття ПЧП	81
6.2. Завдання точки. Завдання прямої. Дійсна величина відрізка прямої. Уклон та
інтервал прямої	81
6.2.1. Завдання точки	81
6.2.2. Завдання прямої	82
6.2.3. Дійсна величина відрізка прямої	83
6.2.4. Уклон та інтервал прямої	83
6.3. Градуювання прямої. Задачі із прямою та її відрізками	84

	5
6.4. Завдання площини. Масштаб уклонів	84
6.5. Перетин двох площин і прямої із площиною	86
6.6. Проекції поверхонь. Завдання топографічних поверхонь. Перетин поверхні із
площиною	87
6.6.1. Проекції поверхонь	87
6.6.2. Завдання топографічних поверхонь	87
6.6.3. Перетин поверхні із площиною	88
6.7. Профіль поверхні	88
РОЗДІЛ 7. КОНСТРУЮВАННЯ ГОРИЗОНТАЛЬНОЇ БУДІВЕЛЬНОЇ ПЛОЩАДКИ
НА ТОПОГРАФІЧНІЙ ПОВЕРХНІ	90
7.1. Мета завдання, зміст та рекомендації щодо оформлення роботи	90
7.2. Приклад виконання графічної роботи	91
7.2.1. Визначення інтервалів укосів виїмки та насипу	91
7.2.2. Побудова лінії перетину прямолінійних укосів земляної споруди	92
7.2.3. Побудова лінії перетину прямолінійного і криволінійного укосів	93
7.2.4. Визначення границь земляних робіт	93
7.2.5. Побудова профілю топографічної поверхні та споруди	95
СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ	97

ВСТУП. МЕТА ТА ЗАДАЧІ КУРСУ

Програма графічної підготовки інженерів містить чотири розділа: “Нарисна геометрія”, “Інженерна графіка”, “Обчислювальна геометрія” та “Комп’ютерна графіка”.

Нарисна геометрія, як геометрія, вивчає просторові форми та співвідношення між ними, як нарисна - застосовує для розв’язання своїх задач мову креслення. Пропонований курс містить у собі елементи точкового опису геометричних форм, що дозволяє нарисній геометрії використовувати, як інструмент, комп’ютер.

Задачами курсу нарисної геометрії є:

1.Навчання майбутнього інженера зображувати об'єкти простору на площині (на плоскому кресленні);

2.Навчання читати плоскі креслення просторових форм (читати просторові форми по системі їх плоских зображень);

3.Навчання розв’язувати задачі із просторовими формами на плоских кресленнях за допомогою спеціальних методів, властивих нарисній геометрії.

РОЗДІЛ 1. ТОЧКА, ПРЯМА, ПЛОЩИНА

1.1. КОМПЛЕКСНЕ КРЕСЛЕННЯ ТОЧКИ І ПРЯМОЇ		А
1.1.1. КООРДИНАТИ І ПРОЕКЦІЇ ТОЧОК. ЕПЮР			Е3
1.1.1. КООРДИНАТИ І ПРОЕКЦІЇ ТОЧОК. ЕПЮР	X		О
(КРЕСЛЕННЯ) Г. МОНЖА		Е1	Е2
			Е2
У Декартової системі координат OE1E2E3	(рис.1.1)		Y
У Декартової системі координат OE1E2E3	(рис.1.1)	Рис.1.1
точка А(x,y,z) визначається трьома дійсними числами x, y, z,		Рис.1.1

що називаються координатами точки А. Одиничний відрізок ОЕ1 визначає вісь абсцис ОХ, одиничний відрізок ОЕ2 визначає вісь ординат OY, а одиничний відрізок ОЕ3 – вісь аплікат OZ. Якщо на осях побудувати прямокутний паралелепіпед з орієнтованими сторонами, рівними координатам точки, то його вершина, протилежна початку координат О, визначить цю точку А.

У нарисній геометрії частіше використовуються не
координати, а проекції точок (рис.1.2) на три взаємо-		П2
перпендикулярні площини проекцій П1,	П2, П3. Ці площини
		A2		П3
називаються:

• Горизонтальна площина проекцій – П1.			A	A3
• Фронтальна площина проекцій – П2.

•Профільна площина проекцій – П3.

	П1
Проекції точки А на ці площини проекцій одержали	A1
відповідні найменування:

•А1 – горизонтальна проекція точки А.

•	А2	– фронтальна проекція точки А.	Рис.1.2
•	А3	– профільна проекція точки А.

Щоб мати можливість використовувати в нарисній геометрії не тільки графічні, але й

обчислювальні методи, зручно за горизонтальну площину проекцій П1 прийняти

координатну площину OXY, за П2 ≡ OXZ, за П3 ≡ OYZ. Тоді точка А і її проекції А1, А2, А3

визначаються декартовими координатами:

A(xA , yA ,zA ); A1 (xA , yA ); A2 (xA ,zA ); A3 (yA ,zA ).

Точку однозначно визначають три її координати. Оскільки будь-яка пара проекцій точки

містить у собі всі три координати, то справедливо, важливе для нарисної геометрії,

твердження:

СИСТЕМА ДВОХ ПРОЕКЦІЙ ТОЧКИ ОДНОЗНАЧНО ВИЗНАЧАЄ ЇЇ ПОЛОЖЕННЯ В

ПРОСТОРІ, ПРИЧОМУ ОДНА З КООРДИНАТ ЗАГАЛЬНА ДЛЯ ДВОХ ПРОЕКЦІЙ.

З’єднавши рис.1.1 і рис.1.2 в один рис.1.3, одержимо просторовий взаємозв'язок

точки, її проекцій і координат. Три взаємо-

перпендикулярні координатні площини, а з

А2

П2

ними три нескінченні площини проекцій

А23

П1, П2, П3 поділяють простір на вісім

частин, що називаються октантами. З

отриманого

нами

твердження,

можна

А3

зробити висновок,

що нарисна геометрія

А12

може використовувати не три,

дві

П3

площини проекцій П1 і П2. Дві площини

проекцій поділяють простір

на

чотири

А1

частини, що називаються чвертями або

А13

квадрантами. Точка А (рис.1.3) знаходиться

П1

в першій чверті, суміжні з нею

– друга

чверть (за фронтальною площиною П2) і

Рис.1.3

четверта чверть (під горизонтальною

площиною проекцій П1). Третя чверть

симетрична першій відносно осі ОХ.

Координата уА відображає віддалення точки А від фронтальної площини проекцій і

називається глибиною точки А, z – відображає висоту

точки А. Точка А12 ОХ, що визначає абсцису точки, а

П2

також орієнтовані

глибина і висота,

що визначають

ординату і аплікату цієї точки, відіграють особливу

роль у нарисній

геометрії. Вони утворюють

епюр

(креслення) Гаспара Монжа – систему двох сполучених

уздовж осі ОХ координатних площин проекцій П1і П2.

A12

При

сполученні площин

проекцій

П1

і П2

обертанням навколо осі абсцис, осі OY і OZ зливаються

П1

в загальну

пряму

лінію, але

мають

різні

напрямки

(рис.1.4). Ланки А12А1 і А12А2

координатної ламаної

Рис.1.4

утворюють пряму А1А2 перпендикулярну осі ОХ, що називається лінією зв'язку. Плоске креслення, що складається з горизонтальної А1 і фронтальної А2 проекцій точки А, розташованих на лінії зв’язку А1А2, перпендикулярної осі проекцій ОХ ≡ х12 має ім'я засновника нарисної геометрії Г. Монжа (рис.1.5).

Монж Гаспар (10.5.1746 – 28.7.1818) – французький геометр і суспільний діяч, чл. Паризької АН (1780). Творець нарисної геометрії, один із творців Політехнічної школи в Парижі. Народився у Бон Кот-д'Ор. Тут закінчив міське училище, а також школу військових інженерів у Мезьере. У 1768 Монжа призначають професором математики, а в 1771 – і професором фізики в цій школі. З 1780 він викладає гідравліку в Луврскій школі (Париж). В ці роки вчений займається математичним аналізом, хімією, метеорологією, практичною механікою. У період Французької буржуазної революції Монж

працював спочатку в місії по встановленню нової системи мір і ваг, а
потім морським інженером і організатором національної оборони. Під			A2
час Директорії Монж зблизився з Наполеоном, брав участь у його

поході в Єгипет і створенні в Каїрі Єгипетського інституту (1798).
Монж одержав всесвітнє визнання, створивши (70-і роки) сучасні	x12		O
методи проекційного креслення і його основу – нарисну геометрію.	x12		O
Однак головний його здобуток з цих питань – “Нарисна геометрія” –
було опубліковано в 1799. Важливі відкриття зробив Монж і в
диференціальній геометрії. Перші його роботи про рівняння поверхонь
були опубліковані в 1770 і 1773. У 1795 і 1801 вийшли у світ його			A1
роботи про кінцеві і диференціальні рівняння різних поверхонь. У
1804 була видана велика книга за назвою “Застосування аналізу до		Рис.1.5
геометрії”. У ній Монж розглядав циліндричні та конічні поверхні,		Рис.1.5

утворені рухом горизонтальної прямої, що проходить через фіксовану вертикальну пряму, канальчасті поверхні, поверхні, у яких лінії

найбільшого нахилу утворюють постійний кут з горизонтальною площиною, поверхні переносу і т.п. Як додаток до книги вчений дав свою теорію інтегрування рівнянь з частковими похідними 1-го порядку і своє розв’язання задачі про коливання струни. Для кожного з видів поверхонь він вивів спочатку диференціальне, а потім і кінцеве рівняння. Він перший позначив буквами p і q часткові похідні від z по x і y, а буквами r, s і t – похідні другого порядку.

У залежності від того, в якій чверті знаходиться точка, її проекції, розташовані на лінії зв’язку, будуть змінювати своє положення відносно осі х12. По положенню проекцій А1, А2 відносно осі, необхідно визначати положення точки А щодо площин проекцій:

•Проекції збігаються і належать осі проекцій точка належить осі.

•Проекції знаходяться над віссю проекцій точка в другій чверті.

•Проекції знаходяться під віссю проекцій точка в четвертій чверті.

•Горизонтальна проекція точки – під віссю, а фронтальна проекція точки – над віссю проекцій точка знаходиться в першій чверті.

•Горизонтальна проекція точки – над віссю, а фронтальна проекція точки – під віссю проекцій точка знаходиться в третій чверті.

•Горизонтальна проекція знаходиться на осі точка належить фронтальної площини проекцій П2.

•Фронтальна проекція точки – на осі точка знаходиться на П1.

Так, по парі проекцій точки, що знаходяться на площині (на аркуші паперу), читають положення точки в просторі (друга задача курсу нарисної геометрії).

І, навпаки, по положенню точки в просторі, зображують її креслення парою проекцій (перша задача курсу нарисної геометрії).

Освоїти перші дві задачі курсу для точки – основна мета вивчаючого курс!

ВПРАВИ:

1.Які чверті при сполученні площин проекцій в одну площину закриваються, а які розкриваються?

2.Якій площині належать точки, проекції яких збігаються?

3.У якій чверті знаходиться точка, координати якої усі негативні?

4.У якій чверті знаходиться точка В, симетрична точці А з першої чверті, відносно х12?

5.Визначити координати точки В, симетричній точці А(20, -10, 30) відносно точки О. У яких чвертях знаходяться точки А і В? Побудувати наочні зображення і епюр Г. Монжа точок А і В.

1.1.2. ЕПЮР ВІДРІЗКА ПРЯМОЇ, ЙОГО НАТУРАЛЬНА ВЕЛИЧИНА ТА КУТИ НАХИЛУ ПРЯМОЇ ДО ПЛОЩИН ПРОЕКЦІЙ (СПОСІБ ПРЯМОКУТНОГО ТРИКУТНИКА).

Якщо з'єднати відрізком прямої однойменні (з однаковими індексами) проекції точок А і В (рис.1.6), то одержимо проекції прямої АВ:

-горизонтальну проекцію А1В1 відрізка АВ,

-фронтальну проекцію А2В2 відрізка АВ.

У загальному випадку проекція відрізка завжди по довжині менше ніж його натуральна величина. Отже, маючи дві проекції відрізка, ми не маємо безпосередньо його натуральної величини. Оскільки дві проекції визначають відрізок, то вони також визначають і його довжину (натуральну величину), що дорівнює гіпотенузі прямокутного трикутника. Один катет такого трикутника дорівнює горизонтальної проекції А1В1 відрізка АВ (рис.1.6), а другий катет по довжині дорівнює різниці висот кінців цього відрізка. Трикутник з гіпотенузою по довжині рівній натуральній величині відрізка побудувати по його проекціях можна на будь-якому вільному місці креслення. Якщо необхідно визначити н.в. одного відрізка, то трикутник прибудовують до однієї з проекцій (рис.1.7), якщо ж спосіб прямокутного трикутника потрібно застосувати багаторазово (визначаються довжини ребер багатогранника і т.п.), то використовують вільне поле креслення.

Зверніть увагу (рис.1.7), що трикутник можна добудувати, як до горизонтальної проекції А1В1, так і до другого катета (різниці висот).

Для зорової наочності введені знаки:

“▐ ” – довжина горизонтальної проекції А1В1; “╢” – довжина фронтальної проекції А2В2; “≡” – різниця висот точок А і В.

“≈” – різниця глибин точок А і В; “н. в. АВ” – натуральна довжина відрізка АВ;

“α” – кут нахилу прямої АВ до горизонтальної площини проекцій П1; “β” – кут нахилу прямої АВ до фронтальної площини проекцій.

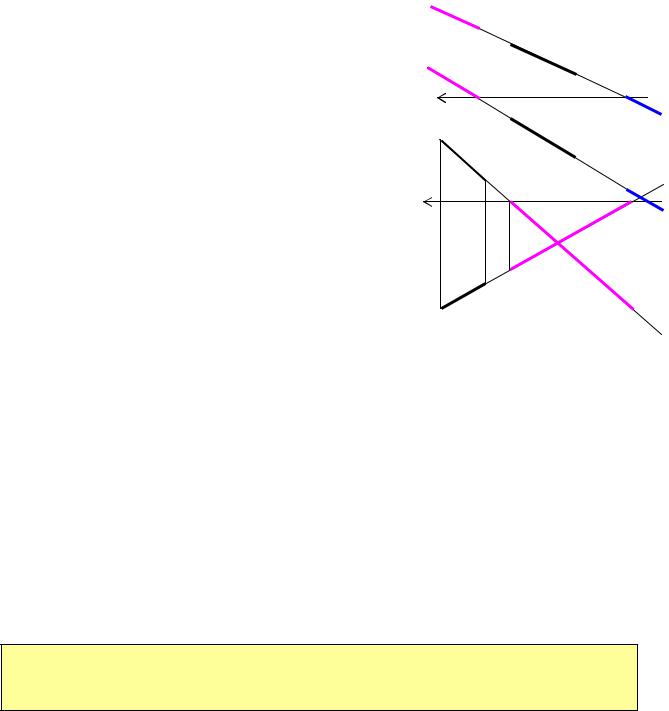
На (рис.1.7) побудовані чотири прямокутних

	А
	≡	В
	≡	α
		В1
	А1	α		≡
		α		≡
А2		н. в. АВ
		н. в. АВ
≡		В2
Х12		В2
Х12
		В1
		≡
	α	н. в. АВ
		н. в. АВ
А1
		Рис.1.6
н. в. АВ		В1
н. в. АВ
	β			н. в. АВ
╢		≡
≈				α
А2		▌		α
А1		╢	β
α	▌	≈	β	н. в. АВ
		≈

		В2
н. в. АВ		≡
	Рис.1.7

трикутники для побудови величин α, β, н.в. АВ. Спосіб побудови таких величин у нарисній геометрії одержав назву від використаної для цього геометричної фігури – спосіб

прямокутного трикутника для визначення довжини відрізка і кутів нахилу прямої до площин проекцій. Це перший спосіб нарисної геометрії, що дозволяє графічно вводити в неї метрику.

1.1.3. СЛІДИ ПРЯМОЇ НА ПЛОЩИНАХ ПРОЕКЦІЙ

Слідом прямої на площині називається точка перетину прямої із площиною. Нас будуть цікавити сліди прямої на площинах проекцій П1 і П2, щоб можна було описати, як розташовується пряма щодо площин проекцій (через які чверті вона проходить). Такий опис називається аналізом прямої.

Горизонтальним слідом називається точка Н перетину прямої з горизонтальною

площиною проекцій.
Нехай задана пряма відрізком АВ, на (рис.1.8)					F2		А2
задані два варіанти її розташування. Потрібно визначити					F2
задані два варіанти її розташування. Потрібно визначити
її сліди Н і F, а також виконати аналіз прямої.				2			В2
її сліди Н і F, а також виконати аналіз прямої.				2
Побудова горизонтального сліду Н:
Побудова горизонтального сліду Н:							1
- фронтальну проекцію А2В2 прямої АВ про-							1		Н2
довжуємо до осі проекцій, одержуємо Н2 (фронтальну				F1
проекцію горизонтального сліду Н);				А2		А1
проекцію горизонтального сліду Н);						А1
- через Н2 перпендикулярно осі проекцій про-									4
- через Н2 перпендикулярно осі проекцій про-								В1	4
водимо лінію зв'язку до перетину з А1В1, одержуємо Н1								В1
водимо лінію зв'язку до перетину з А1В1, одержуємо Н1									Н1
(горизонтальну проекцію горизонтального сліду)				В2			Н2		Н1
Фронтальним слідом називається точка F							Н2			F1
перетину прямої з фронтальною площиною проекцій.				1		4				F1
Для прямої АВ (рис.1.8) потрібно визначити				1
Для прямої АВ (рис.1.8) потрібно визначити
фронтальний слід (два варіанти розташування прямої).										3
Побудова фронтального сліду F:			АВ	В1			Н1
- горизонтальну	проекцію	А1В1 прямої	АВ							F2
продовжуємо до осі	проекцій,	одержуємо	F1	А1						F2
продовжуємо до осі	проекцій,	одержуємо	F1	А1
(горизонтальну проекцію фронтального сліду);
- через F1 перпендикулярно осі проекцій							Рис. 1.8
проводимо лінію зв'язку до перетину з А2В2, одержимо F2
(фронтальну проекцію фронтального сліду).

Аналіз прямої АВ (перший варіант):

-відрізок прямої АВ між слідами F і Н знаходиться в першій чверті;

-пряма АВ, перетинаючи верхню частину фронтальної площини, іде променем у другу чверть;

-пряма АВ, перетинаючи передню частину горизонтальної площини, іде променем у четверту чверть.

Остаточно аналіз проходження прямої має вигляд:

Пряма, виходячи з другої чверті, перетинає верхню частину фронтальної площини входячи в першу чверть, потім перетинаючи передню частину горизонтальної площини, іде в четверту чверть.

Вправа: Виконати аналіз прямої АВ (другий варіант).

Відповідь: Пряма, виходячи з першої чверті перетинає передню частину горизонтальної площини, входить у четверту чверть, потім перетинає нижню частину фронтальної площини, уходить у третю чверть.

1 / 101 2 3 4 5 6 7 8 9 10 > Следующая >>>

Соседние файлы в папке конспекты

#
21.02.20161.83 Mб20------_-----.pdf
#
21.02.2016441.9 Кб17---.---.1-- -.--.pdf
#
21.02.2016706.64 Кб23---_-------_Excel (1).pdf
#
21.02.2016706.64 Кб20---_-------_Excel.pdf
#
21.02.20164.64 Mб43123.pdf
#
21.02.20161.55 Mб201234.pdf
#
21.02.2016855.41 Кб32end_3.pdf