
конспекты / 1234
.pdf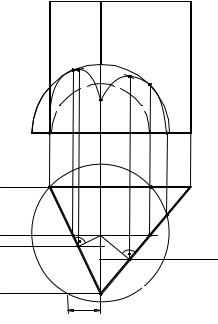
51
Фронтальною межею видимості для лінії перетину буде лінія головних меридіанів заданих поверхонь, а тому що частина лінії перетину від точки 1 до точки 5 знаходиться перед цією межею, те фронтальна проекція цієї частини лінії перетину буде видимою.
3.5.1.б. СПОСІБ ФРОНТАЛЬНИХ СІЧНИХ ПЛОЩИН
Приклад 3. Побудувати лінію перетину півсфери і прямої трикутної призми (рис.3.20).
|
|
|
|
|
|
Оскільки призма займає фронтально-проектуюче |
||||||
|
|
|
|
|
|
положення, то фронтальна проекція 12 лінії перетину l |
||||||
|
5 |
3 |
426 |
|
півсфери |
призмою відома: |
вона |
збігається |
з |
|||
|
|
фронтальним окресленням призми. |
|
|
|
|||||||
|
2 |
2 |
|
|
|
|
||||||
|
|
|
22 |
2 |
|
Геометричний алгоритм розв’язання прикладу |
||||||
|
|
|
|
|
||||||||
|
12 |
|
|
8272 |
|
3 способом фронтальних січних площин |
|
|
|
|||
|
|
|
|
1. |
Використовуємо, |
як |
посередників, |
|||||
I1 |
11 |
|
a1 |
81 |
|
фронтальні площини |
рівня. Тоді |
точки, |
що |
|||
|
|
належать лінії перетину, будуть визначаться на |
||||||||||
|
|
|
R' |
71 |
|
|||||||
V |
5 |
|
|
|
перетині півкіл із прямими, по яких обране |
|||||||
III11 |
1 |
|
|
61 |
IV1 |
сімейство площин буде перетинати задані поверхні. |
||||||
|
31 |
c1 |
|
2. Приймемо, як опорні точки − |
точки |
|||||||
II |
b1 |
|
|
|||||||||
21 |
Рис.3.20 |
зломів, |
екстремальні |
по |
висоті точки і |
точки |
||||||
1 |
|
R' |
головного меридіана на півсфері. |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||
Січна площина I перетинає півсферу по півколу a, горизонтальна проекція якої збігається з горизонтальним окресленням призми. Січну площину II проводимо через ребро призми, перетинаючи півсферу по півколу b, що у свою чергу перетинається з ребром призми в точці 2.
Для завдання найвищих точок лінії перетину поверхонь, опустимо перпендикуляри з проекції O1 центра півсфери на відповідні проекції горизонтально-проектуючих граней призми. Через отримані горизонтальні проекції 31, 41 проведемо горизонтальні сліди фронтальних площин-посередників III і IV.
Січна площина III перетинає грань призми по фронтально-проектуючій прямій, що проходить через точку 3, а півсферу по півколу c, фронтальні проекції яких, в свою чергу, перетинаються в точці 32. Аналогічно одержуємо фронтальну проекцію точки 4.
Січна площина V проходить через головний меридіан півсфери, перетинаючи при цьому призму по горизонтально-проектуючих прямих, що проходять через точки 5 і 6. Фронтальні проекції 52 і 62 будуть знаходитися на перетині фронтальних окреслень півсфери і ліній перетину січної площини з гранями призми.
Основи заданих поверхонь належать площини П1 і тому вони перетинаються в точках 1, 6, 5, що є самими низькими точками лінії перетину заданих поверхонь. Їхні горизонтальні проекції 11, 71, 81 будуть знаходитися на горизонтальних проекціях основ півсфери і призми, а фронтальні проекції 12, 72, 82 – на фронтальній проекції основ.
52
3. Визначення видимості фронтальною межею видимості є лінії головного меридіана півсфери. Тому на фронтальній площині проекцій повинна бути видимої тільки частина лінії перетину, розташована перед фронтальним меридіаном. Таким чином, на фронтальній площині проекцій П2 будуть видимі частини лінії, обмежені точками 5, 2 і 2, 6.
3.5.1.в. СПОСІБ ПРОЕКЦІЮЮЧИХ ПЛОЩИН
|
|
|
|
S2 |
|
|
|
|
|
|
Приклад |
4. |
Побудувати проекції |
лінії |
||||
|
|
|
|
|
|
|
|
|
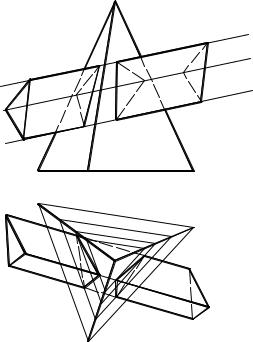
перетину тригранної піраміди і призми (рис.3.21). |
|||||||||
|
|
|
|
|
|
|
|
|
I2 |
|||||||||
|
|
|
|
|
|
|
|
E' |
|
Геометричний алгоритм розв’язання |
||||||||
E |
2 |
K |
K'2 |
32 |
|
2 |
II2 |
прикладу 4 способом проектуючих площин |
||||||||||
1 |
|
|
22 |
|
|
D'2 |
|
|
|
|
|
|
|
|
|
|
||
2 |
42 |
|
|
2 |
M' 62 |
|
III2 |
|
1. Використовуємо для розв’язання задачі |
|||||||||
|
|
|
52 |
|
|
|||||||||||||
D2 |
M |
|
82 |
|
2 |
2 |
F' |
|
сімейство |
фронтально-проектуючих |
площин, |
|||||||
72 |
2 |
|
L'2 |
|
9 |
2 |
|
рівнобіжних ребрам призми. Кожна з цих площин |
||||||||||
L2 |
|
|
|
|
|
|||||||||||||
F2 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
буде перетинати піраміду по трикутнику і точки |
|||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||
A2 |
B2 |
|
|
|
|
C2 |
|
лінії |
перетину |
будуть визначатися |
на |
перетині |
||||||
|
|
|
|
|
цього трикутника з ребром призми. |
|
|
|
||||||||||
D1 A1 |
71 41 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
1 |
|
|
1 |
91 |
C1 |
|
|
|
2. |
|
Задамо опорні |
точки |
лінії |
||||
E1 |
M1 |
1 |
S1 |
31 6 |
|
|
|
|
перетину. |
|
|
|
|
|
||||
F1 |
|
|
K1K' |
M' |
D'1 |
|
|
Нехай фронтально-проектуюча площина I |
||||||||||
L1 |
121 |
1 |
|
1 |
E' |
|
|
|||||||||||
|
|
|
|
|
перетинає |
піраміду |
по |
трикутнику 123. |
Тоді |
|||||||||
|
5 |
L'1 |
|
|
1 |
|
горизонтальні проекції K1 і K’1 точок перетину K |
|||||||||||
|
81 |
|
|
|
F'1 |
|
||||||||||||
|
B1 |
|
|
|
|
і K’ |
піраміди |
ребром |
призми |
EE’ |
будуть |
|||||||
|
Рис.3.21 |
|
|
|||||||||||||||
|
|
|
знаходитися на перетині горизонтальної проекції |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
112131 трикутника 123 з горизонтальною проекцією E1E’1 ребра EE’, а фронтальні проекції K2 і K’2 цих точок можна знайти, використовуючи властивість належності.
Аналогічно визначимо точки L, L', M, М' лінії перетину призми з пірамідою. З'єднавши отримані точки прямими, лінію перетину.
3.Визначимо видимість лінії перетину.
Оскільки усі відрізки, що складають частини лінії перетину, належать як граням призми, так і граням піраміди, то їхня видимість цілком визначається видимістю цих граней. Так, на горизонтальній площині проекцій усієї грані піраміди видимі, а з граней призми невидима тільки одна – DD'F'. Тому на горизонтальній площині проекцій невидимі тільки відрізки L1M1 і L'1M'1, що належать лінії перетину.
На фронтальній площині проекцій видимими є дві грані піраміди – ASB і BSC, а також одна грань призми – ЕЕ'F'. Тому видимими будуть тільки відрізки K2L2 і K'2L'2, що належать цій грані призми.
Задача по побудові лінії перетину граних поверхонь, коли одна з них є проектуючою, вирішується зовсім просто: по точках перетину ребер одного багатокутника з гранями іншого – спосіб ребер; або по лініях перетину граней одного багатокутника з гранями іншого
– спосіб граней.

53
3.5.2. СПОСІБ СФЕР ПРИ ПОБУДОВІ ЛІНІЇ ПЕРЕТИНУ ПОВЕРХОНЬ ОБЕРТАННЯ
3.5.2.а. СПІВВІСНІ ПОВЕРХНІ ОБЕРТАННЯ І ЇХ ЛІНІЇ ПЕРЕТИНУ
Для визначення лінії перетину двох поверхонь обертання доцільно скористатися однією властивістю цих поверхонь. Воно полягає в тому, що
дві співвісні поверхні, тобто поверхні, що мають загальну вісь, перетинаються по колах, які проходять через точки перетину меридіанів поверхонь.
На рис.3.22 таких точок одна - Q, на рис.3.23 – дві: M і N і стільки ж відповідних їм ліній перетину: q, m, n.
|
|
i |
α |
≡ |
β |
2 |
α2≡ β2 |
2 |
i |
|
|||
|
|
|
|
|
||
i |
i |
m2 |
|
|
M2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
q |
2 |
Q2 |
n2 |
|
|
N2 |
|
|
|
|
|||
|
|
|
|
|
|
|
Рис.3.22
Рис.3.23
На рисунках ці кола зображені відрізками прямих, що є фронтальними проекціями паралелей, по яких перетинаються поверхні обертання.
3.5.2.б. ПЕРЕТИН ПОВЕРХОНЬ ОБЕРТАННЯ І СФЕРИ З ЦЕНТРОМ НА ОСІ ОБЕРТАННЯ В окремому випадку, якщо одна з поверхонь обертання – сфера, приведене вище
властивість може бути сформульована інакше, а саме:
якщо центр січної сфери знаходиться на осі поверхні обертання, то сфера перетне дану поверхню по колах, число яких дорівнює числу точок перетину головних меридіанів поверхні
(рис.3.24).
|
|
|
|
iα2 |
|
|
|
Якщо вісь поверхні обертання перпендикулярна площині |
||||
|
|
|
|
|
|
|
проекцій П1 (або П2), то кола проектуються на площину П1 (або П2) |
|||||
|
|
|
|
m2 |
|
|
|
без спотворення, а на площину П2 (або П1) у відрізки прямих, |
||||
|
|
|
|
|
|
M2 перпендикулярних фронтальній (горизонтальній) проекції осі |
||||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||
Р |
|
|
O2 |
|
|
|
обертання (див. рис.1…3) |
|
|
|||
|
|
|
|
|
Поверхня сфери може перетинатися по колу з будь якою |
|||||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
співвісною |
поверхнею обертання, |
що |
має сімейство кіл, |
|
|
|
|
n2 |
N2 |
|
наприклад, |
з циліндричною поверхнею, |
конічною поверхнею |
|||
|
|
|
|
|
|
|
другого порядку, та ін. |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
РЗастосування сфер у якості допоміжних січних поверхонь
Рис.3.24 |
становить особливий інтерес, тому що будь-яка площина, що |
|
54
проходить через центр сфери, є площиною симетрії, на сфері може бути узята нескінченна безліч систем кіл, і проекція сфери будується дуже просто. Ці обставини дозволяють з достатнім ступенем точності будувати лінії перетину поверхонь обертання за допомогою допоміжних сфер.
Сфери-посередники проводяться або з одного загального для всіх сфер центра (спосіб концентричних сфер), або – з різних центрів (спосіб ексцентричних сфер). В останньому випадку радіуси сфер можуть бути рівними або різними.
Особливості кожного з цих способів і умови його застосування простежимо на конкретних прикладах.
3.5.2.в. СПОСІБ КОНЦЕНТРИЧНИХ І ЕКСЦЕНТРИЧНИХ СФЕР ПРИ ПОБУДОВІ ЛІНІЇ ПЕРЕТИНАННЯ ПОВЕРХОНЬ ОБЕРТАННЯ
СПОСІБ КОНЦЕНТРИЧНИХ СФЕР
Цей спосіб застосовується для побудови лінії перетину двох поверхонь обертання, осі яких перетинаються. Він заснований на співвісності поверхонь.
Центр допоміжної січної сфери повинний лежати в точці перетину осей поверхонь. Для спрощення графічного розв’язання необхідно, щоб площина, утворена осями
поверхонь обертання, була паралельна до якої-небудь площини проекцій.
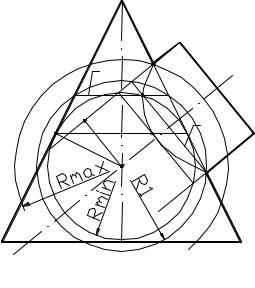
Приклад 1. Побудувати лінію перетину конічної і циліндричної поверхонь обертання з перетинними осями (рис.13.25.
12
a2
22
N'2 N2 32 b2 O2
42
Рис.3.25Р
Побудуємо довільну сферу радіуса R1 з центра O(O2), що на кресленні зобразиться колом з центром O2. Ця сфера співвісна як з однією, так і з другою поверхнею, а тому вона перетне їх по колах.
Позначимо кола перетину, зображені на кресленні відрізками прямих, відповідно як a2 і b2.
В перетинанні кіл одержимо точку 22, що належить обом даним поверхням і, отже, до шуканої лінії перетину. Проекції таких точок є точками перетину проекцій кіл.
Змінюючи радіус допоміжної сфери і виконуючи аналогічні побудови, одержимо інші проміжні точки лінії перетину поверхонь.
Перед тим як проводити кола, що зображують довільні сфери, потрібно з'ясувати розміри радіусів найбільшої та найменшої сфер, придатних для розв’язання даної задачі. Для цього треба визначити точки перетину окреслювальних утворюючих поверхонь. Відрізок, що представляє відстань найбільш віддаленої проекції точки (12) від проекції центра (O2), буде радіусом найбільшої сфери. Для визначення радіуса найменшої сфери потрібно з точки O2 провести дві нормалі до окреслювальних ліній поверхонь. Визначивши точки перетину N2 і N’2 нормалей з окреслювальними лініями, потрібно взяти більший із двох отриманих

55
відрізків. Якщо взяти як радіус допоміжної сфери менший відрізок, то одна з даних поверхонь з такою сферою не перетнеться.
Таким чином, сфера мінімального радіуса повинна до більшої поверхні, перетинаючи меншу. Максимальний радіус сфери -це відстань від центра сфери до найбільш віддаленої точки перетину окреслень поверхонь.
Геометричний алгоритм розв’язання задачі
1.Визначаємо опорні точки (1 і 4) перетину окреслень поверхонь.
2.Визначаємо центр концентричних сфер (точка перетину осей – O(O2)).
3.Визначаємо мінімально допустиму сферу на основі проведення нормалей до нарисових ліній поверхонь і вибору більшого з двох відрізків.
4. Будуємо точки лінії перетину за допомогою мінімальної сфери – (3(32)).
5.Визначаємо максимально припустиму сферу, беручи в якості радіуса відстань до найбільш віддаленої проекції точки.
6.Проводимо проміжну сферу:
а) будуємо перетин першої поверхні і сфери (a(a2)); б) будуємо перетин сфери з другою поверхнею (b(b2));
7.Визначаємо проміжну точку 2(22).
8.Будуємо лінію перетинання поверхонь, з'єднуючи отримані точки плавної кривої по лекалу.
Лінія перетину, у цьому прикладі, розпалася на дві частини просторової кривої. В наслідок загальної площини симетрії в фігурах, що перетинаються, проектуються на цю площину (або паралельну їй площину) у виді кривої другого порядку. Якщо ж потрібно
|
побудувати проекції цієї лінії на інші площини, |
|
|
то це легко зробити, зв'язавши кожну точку лінії |
|
C2 |
перетину з колом, що лежить на тій чи іншій |
|
A2 |
поверхні обертання. |
|
|
Розглянемо варіант, коли мінімальна сфера |
|
O2 |
дотикається до двох поверхонь обертання. У |
|
цьому випадку для побудови лінії перетину |
||
B2 |
||
поверхонь використовується теорема Г. Монжа, |
||
D2 |
що формулюється так: |
|
Якщо дві поверхні другого порядку описані |
||
Рис.3.26Р |
біля третьої або вписані в неї, то лінія їхнього |
|
перетину розпадається на дві плоскі криві |
другого порядку. Площини цих кривих проходять через пряму, що з'єднує точки перетину ліній дотику.
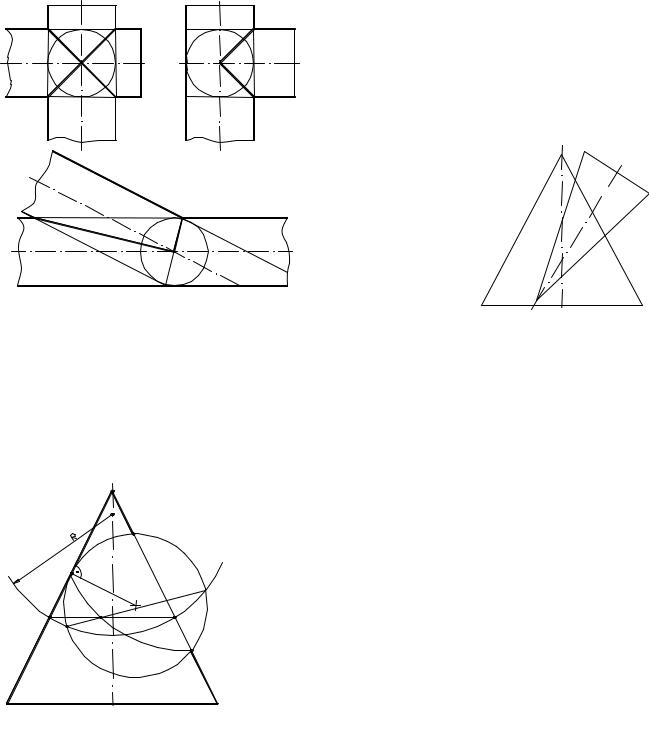
Відповідно до цієї теореми лінії перетину конуса і циліндра, описаних навколо сфери (рис.15), будуть плоскими кривими – еліпсами, фронтальні проекції яких зображуються прямими A2B2 і C2D2.
|
|
|
|
56 |
|
Теорема |
Монжа |
знаходить |
ефективне |
|
застосування |
при |
конструюванні |
|
|
трубопроводів. Можливість вписування сфери в |
|||
|
циліндри однакового діаметра дозволяє дуже |
|||
|
швидко запроектувати їх перетин (рис.16). |
|||
|
|
|
iα2 |
|
|
Вправа: |
|
|
|
|
Побудувати |
|
|
|
|
перетин двох |
конусів |
|
|
|
обертання, осі яких |
|
|
|
|
перетинаються |
і |
|
|
Рис.3.27 |
паралельні |
П2 |
|
|
(рис.3.28). |
|
|
|
|
Ри |
|
iβ2 |
Рис.3.28 Р |
|
|
|
|
||
СПОСІБ ЕКСЦЕНТРИЧНИХ СФЕР
Цей спосіб може бути використаний для побудови лінії перетину двох поверхонь, що мають загальну площину симетрії. При цьому кожна поверхня повинна мати сімейство кіл. Як і в способі концентричних сфер, площина симетрії повинна бути паралельна однієї з
i2 площин проекцій. Сутність способу легко усвідомити з наступних прикладів.
|
|
12 |
|
22 |
|
A2 |
42 |
B2 |
|
C2 |
32 |
|
|
Рис.3.29
Приклад 1. Побудувати лінію перетину конуса зі сферою (рис.3.29).
Вісь конуса і центр сфери розташовані в одній фронтальній площині. Будь-які дві сфери перетинаються по колу. Тому, якщо ми візьмемо будь-як допоміжну сферу радіуса R з центром на осі конуса, то вона перетне і дану сферу і даний конус по колах. У перетині цих кіл ми одержимо точки лінії перетину даних поверхонь. Для побудови наступних точок можна брати інші допоміжні сфери з різними положеннями центрів на осі конуса.
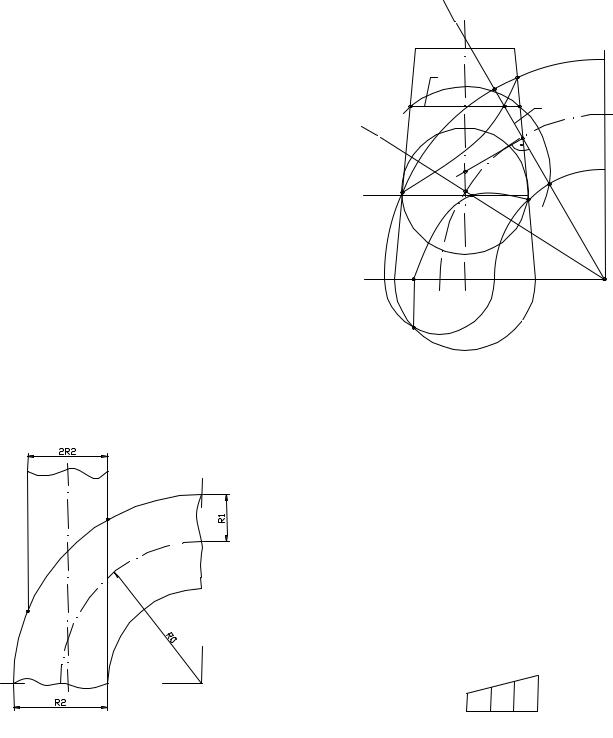
Приклад 2. Побудувати лінію перетину конуса з кільцем (рис.3.30). Геометричний алгоритм рішення задачі
1.Задамо загальну площину симетрії поверхонь, що проходить через вісь конуса i(i2), середню лінію кільця і співпадаючу з площиною середньої лінії кільця.
2.Визначимо опорні точки 1(12), 2(22), 3(32), 4(42).
3.Проведемо через вісь кільця l2 допоміжну фронтально - проектуючу площину
τ(τ2) для побудови довільних точок лінії перетину. Ця площина розсіче кільце по колу, проекцією центра якої буде точка O2.
|
|
57 |
4. |
Проведемо із центра O(O2) перпендикуляр до площини отриманого кола. Цей |
|
перпендикуляр буде дотичною до середньої лінії кільця. |
|
|
5. |
Визначимо точку перетину перпендикуляра й осі конуса – точку K(K2). |
|
6. |
Прийнявши точку K(K2) за центр сфери, проведемо таку сферу, на якій лежало |
|
би коло з центром O(O2). Для зображення такої сфери необхідно провести коло з центром |
||
K(K2), що проходить через кінці відрізка a2, що зображує коло з центром O(O2). |
||
7. |
Проведемо відрізок b2, що зображує |
τ2 |
коло перетинання сфери і конуса. |
i2 |
|
8.Визначимо точку 5(52) перетину
отриманих кіл і приналежну одночасно конусові і |
|
b2 |
|
22 |
|||
кільцю, і тому є точкою шуканої лінії їх |
|
|
|
||||
|
|
|
a2 |
||||
перетину. |
Аналогічною |
побудовою, |
τ'2 |
52 |
|||
9. |
|
|
02 |
||||
застосовуючи нові допоміжні площини, знайдемо |
|
K2 |
|
||||
|
|
|
|||||
необхідну |
кількість |
точок лінії перетину. При |
|
|
|
||
12 |
K'2 6 |
2 |
|
||||
цьому потрібно проводити допоміжні сфери з |
|
||||||
|
32 |
||||||
різних центрів, що лежать на осі конуса. |
|
|
|
||||
Таким |
чином, |
перевагою |
способу |
|
42 |
|
L2 |
ексцентричних сфер є те, що його можна |
|
|
|||||
|
|
|
|||||
застосовувати і в тих випадках, коли одна з |
|
|
|
|
|||
пересічних поверхонь не є поверхнею обертання. |
|
|
|
Рис.3.30 |
|||
Необхідною |
умовою є |
наявність на |
цій поверхні |
|
|
|
|
сімейства кіл, які можна розглядати як результат перетину поверхні зі сферою. У число умов входить також умова, щоб перпендикуляри, встановлені з центрів кругових перетинів, перетинали вісь поверхні обертання.
Вправа:
На рисунку 3.31 зображений елемент трубопроводу. Його поверхня циліндрична. Необхідно побудувати лінію перетину цієї поверхні з поверхнею циліндричної труби способом ексцентричних сфер.
Закон зміни радіуса перетину циліндричної поверхні.
R2 R
Рис.3.31

58
РОЗДІЛ 4. ОСНОВИ ОБЧИСЛЮВАЛЬНОЇ ГЕОМЕТРІЇ.
4.1. ПОДІЛ ВІДРІЗКА В ЗАДАНОМУ ВІДНОШЕННІ.
При розв’язанні задач у нарисній геометрії може виникати задача поділу відрізка АВ, заданого
своїми проекціями А1В1 і А2В2 у деякому відношенні. Для |
|
|
В2 |
рішення цієї задачі застосовується теорема ФАЛЕСА (одна |
|
|
|
|
|
||
з теорем елементарної геометрії): “якщо на одній зі сторін |
|
|
|
кута від його вершини послідовно відкласти рівні між |
А2 |
С2 |
|
собою відрізки і через кінці цих відрізків провести |
|
|
|
рівнобіжні прямі, що перетинають другу сторону кута, то |
|
|
|
|
|
|
|
на другій стороні кута відкладуться також рівні між собою |
|
|
|
відрізки”. |
|
|
|
ФАЛЕС Мілетський (біля 625 – 547 до н.е.) |
|
|
|
Давньогрецький математик і астроном. У молодості Фалес |
|
|
|
відвідав Єгипет, де в школах Мемфіса і Фів вивчив різні |
|
|
|
науки. Повернувшись на батьківщину, заснував у Мілеті |
|
|
|
філософську школу. |
А |
С1 |
|
Історики вважають, що Фалес перший познайомив |
1 |
|
В1 |
|
|
греків з геометрією і що він був першим грецьким |
|
|
астрономом. Фалес пророчив сонячне затемнення, що мало |
Рис.4.1 |
|
місце 28 травня 585 до н.е. Знання Фалеса в геометрії були |
||
|
досить широкими. Він знав, що протилежні кути, що утворюються при перетині двох прямих, рівні; що в рівнобедреному трикутнику кути, що лежать при основі, рівні; що трикутник цілком визначається двома кутами та прилеглою до них стороною і що на підставі цього можна визначати відстань корабля від берега; що коло поділяється діаметром навпіл (сам довів це твердження); що кут, вписаний у півколо, - прямій. Фалесу приписують також спосіб визначення висот різних об’єктів, зокрема пірамід, по тіні, коли сонце піднімається над обрієм на 45º.
Оскільки відношення відрізків, розташованих на прямій є інваріантом паралельного проектування (не змінюється при паралельному проектуванні), тоді для поділу відрізка на епюрі досить розділити в потрібному відношенні одну з його проекцій (на рис. 1 поділена горизонтальна проекція А1В1), а потім по лінії зв’язку визначається
точка на другій проекції відрізка ( на А2В2 точка С2).
4.2. ОБЧИСЛЕННЯ ТОЧКИ ПО ЗАДАНОМУ ВІДНОШЕННЮ. РІВНЯННЯ ПРЯМОЇ.
Якщо кінці відрізка задані координатами А(хА, yА, zА), B(xВ, yА, zА) і АС/AB = λ, тоді точкове числення дозволяє обчислити точку С:
ACAB = AA−−CB = λ A −C = λ(A−B) C = (B−A)λ+A
Точкове числення передбачає покоординатний розрахунок точок, отже, маємо координати шуканої точки С:
xC =(xB −xA )λ+xA C = (B−A)λ+A yC =(yB −yA )λ+yA .
zC =(zB −zA )λ+zA
59
При λ = ½ точка С поділить відрізок навпіл (С – центроїд відрізка), тоді будемо мати:
C = A2+B
Якщо відношення λ прийняти як параметр t, що приймає значення з області дійсних чисел, тоді поточна точка М прямої АВ визначить точкове рівняння прямої:
xC =(xB −xA )t+xA M = (B−A)t +A yC =(yB −yA )t+yA .
zC =(zB −zA )t+zA
Або, в іншому виді:
M = At +Bt, t =1- t.
Доповнення параметра до одиниці зручно використовувати при завданні точкового рівняння прямої.
4.3. РІВНЯННЯ ПРЯМОЇ ЛІНІЇ, ВІДРІЗКА, ПРОМЕНЯ В СТАНДАРТНІЙ ТА ПРИРОДНІЙ ПАРАМЕТРИЗАЦІЯХ.
Оскільки параметр t = АМ/AB, тоді доповнення параметра до одиниці має вигляд:
t =1−t =1− AMAB = ABAB−AM = MBAB .
Тоді, останнє точкове рівняння прямої можна записати у вигляді:
M = A×MB+B×AM = Aa+Bb , AM+MB a+b
де a і b симетричні параметри з області дійсних чисел, що задовольняють залежності:
а + b =const = lAB.
Параметри a і b називаються стандартними, а рівняння – рівнянням прямої у стандартній параметризації.
А М В
b |
а |
|
lAB |
Рис. 4.2
У точковому численні прийнято позначати параметр t через q, а його доповнення до одиниці – через р. Рівняння прямої, записане у вигляді:
M = Ap + Bq,
де p + q = 1,
називається рівнянням прямої АВ у природній параметризації.
Існує безліч і інших параметризацій прямої, кожна з яких пристосована до розв’язання певного виду задач, але природна і стандартна параметризації складають основу точкових рівнянь. Щоб задати точку С на прямій АВ досить задати її параметри (наприклад рс і qc, причому pc + qc =1 або ac і bc, де ac + bc = lAB). Щоб задати відрізок або промінь на

60
прямій досить вказати область зміни параметрів. Задамо, наприклад, значення параметра t для різних геометричних форм:
Значення параметра t |
Геометрична форма |
|
Параметр t |
дорівнює нулю (t = 0) |
Точка А |
Параметр t дорівнює одиниці (t = 1) |
Точка B |
|
Параметр t |
приймає значення |
|
від 0 до 1 (0 ≤ t ≤1) |
Відрізок AB |
|
Параметр t |
більше або дорівнює 0 (t ≥ 0) |
Промінь із А спрямований до B |
Параметр t |
менше або дорівнює 0 (t ≤ 0) |
Промінь із А в напрямку зворотному B |
Параметр t |
більше або дорівнює 1 (t ≥ 1) |
Промінь із B у напрямку зворотному А |
Параметр t |
менше або дорівнює 1 (t ≤ 1) |
Промінь із B у напрямку А |
Параметр t |
належить числовій |
|
осі (– ∞ < t < ∞) |
Пряма АB |
|
4.4. ПОБУДОВА ЧЕТВЕРТОЇ ВЕРШИНИ ПАРАЛЕЛОГРАМА ПО ТРЬОМ ЗАДАНИМ. РІВНЯННЯ ПЛОЩИНИ.
Нехай задані три вершини A, B, C паралелограма |
|
А |
D |
|
ABCD. Потрібно визначити току D (четверту |
вершину |
|||
|
K |
|||
паралелограма). |
|
|
||
|
|
|
||
Точка К (рис. 3) є центроїдом діагоналей паралелограма: |
B |
C |
||
2К = А + С = В + D D = A + C – B. |
|
|||
Твердження: Вершина паралелограма дорівнює сумі двох |
|
Рис. 4.3 |
||
суміжних з нею вершин без протилежної вершини. |
|
|
|
|
Задача. Визначити рівняння прямої, яка паралельна АВ і проходить через точку С. Розв’язання: Поточна точка М шуканої прямої утворить з поточною точкою N прямої
АВ паралелограм ANMC (рис. 4). Рівняння прямій АВ в |
C |
M |
|
природній параметризації має вигляд: |
|
||
|
|
||
N = Ap + Bq, |
|
N |
B |
тоді шукана вершина М паралелограма ANMC визначить |
|
||
шукане рівняння: |
|
А |
|
М = Ap + Bq + C – A = A (p - 1) + Bq – C, |
|
|
|
де p + q = 1. |
|
Рис. 4.4 |
|
