УЧЕБНО-МЕТОДИЧ. ПОСОБИЕ ПО ВМ_1

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Белорусский государственный экономический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

у прямых L1 и L2 известны направляющие векторы

1 m1; n1 ; p1

; n2 ; p2 соответственно.

.pdf

Скачиваний:

Добавлен:

20.02.2016

Размер:

2.05 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 109 10 > Следующая >>>

Решая эту систему, находим х 1, у 3 . Итак, на прямой известна точка

M 0 1;

; 0

. Так как направляющий вектор s (l;m; p) должен быть перпен-

дикулярен к нормальным векторам n1 (1;2; 3)

и n2 (2; 2;1)

заданных плос-

костей, то

, т.е.

, R .

4 ; 7 ; 6 . Со-

Тогда

n1 n2

4i 7 j 6k ,

x 1

z 0

x 1

– канониче-

гласно формуле (3.28)

или

ские уравнения прямой.

Из канонического уравнения прямой видно, что направление прямой зада-

ет вектор

4; 7; 6 .

Он образует с координатными осями Ox, Oy, Oz углы

, и

соответственно. Находим направляющие косинусы:

cos

, аналогично cos

, cos

42 72 62

101

Заметим, что равенство cos2 cos2 cos2 1 выполняется.

П р и м е р 3.9. Составить параметрические уравнения прямой, проходя-
щей через точку М 0	2; 1; 3 , в каждом из следующих случаев:
	х 1 2t,
		t R;
а) параллельно прямой y 2 4t,		t R;

	z t,

б) параллельно оси Oy ;

в) перпендикулярно плоскости 3x y z 8 0 .

Р е ш е н и е а) Так как прямые параллельны, то они имеют один и тот же направляю-

щий вектор s 2; 4;1 .

Согласно формуле (3.29), составим параметрические уравнения прямой:

		х 2 2t,
					t R .
		y 1 4t,

		t 3 t,
	б) В	качестве направляющего вектора оси Oy можно взять вектор
	0;1; 0	, совпадающий с ортом		.
s			j

Искомые уравнения прямой

õ 2 0 t,		õ 2,
			t,	t R.
y 1	1 t, или y 1		t,	t R.
	0 t
z 3	0 t	z 3;

в) Вектор п 3;1; 1 перпендикулярен плоскости 3x y z 8 0 . Следовательно, в качестве направляющего вектора прямой можно взять

вектор n, т. е. s 3;1; 1 . Тогда параметрические уравнения прямой примут вид

	õ 2 3t,
		t,	t R.
	y 1
		t,
	z 3
П р и м е р 3.10. Составить канонические уравнения прямой, проходящей
через точку М 0 4; 3; 2	параллельно:

а) вектору а 3; 6; 5 ;

х 3у z 6 0,

б) прямой

2х у 4z 1 0.

Р е ш е н и е а) В качестве направляющего вектора прямой, проходящей через точку

М 0 , возьмем вектор s , равный вектору a , т. е. s 3; 6; 5 . Тогда по формуле (3.28) канонические уравнения прямой примут вид

x 4

у 3

z 2

б) Так как направляющий вектор s (l;m; p)

должен быть перпендикуля-

рен к нормальным векторам n1 (1;3;1) и n2

(2; 1; 4) заданных плоскостей,

то

, т.е.

, R .

11 ; 6 ; 7 или

Тогда n1 n 2 1

1 11i 6 j 7k

s 11; 6; 7 .

Так как данная прямая и искомая параллельны между собой, то в качестве направляющего вектора s1 искомой прямой можно взять вектор s , т. е. s1 s . Получаем канонические уравнения

x 4	у 3	z 2	.
11
	6	7

3.5.1 Задачи для самостоятельного решения

1. Найти канонические уравнения прямой,

проходящей через точку

М 3; 2; 5 параллельно:

а) оси Ох; б) оси Оу; в) оси Оz;

г) прямой

х у z 1 0,

4z 3 0;

2х

д) прямой

x 1

у 1

х 2,

2. Найти направляющий вектор прямой

z 4.

х 2 у 4z 8 0,

3. Привести к каноническому виду прямую

3у 2z 18 0.

6х

4. Найти направляющие косинусы прямой

x 3

у 2,5

z 1

5. Найти параметрические уравнения прямой:

а)

проходящей

через

точку М 0

1; 0; 1

параллельной вектору

2; 3; 0

;

б) проходящей через точки М1 2; 2; 2

и М 2 6; 2;1 .

6. Составить канонические уравнения прямой, проходящей через две дан-

ные точки:

а) М1

1; 4; 8 , М 2 1; 3; 0 ;

б) М1

2; 1;10 , М 2 2; 3; 5 .

7. Найти расстояние от точки М 0 1; 2; 4 до прямой:

а)

x 1

у 3

z 4

;

х t,

б) y 1 3t,

t R ;

z 5 t

х у z 1 0,

в)

4х у z 11

8. Найти расстояние между скрещивающимися прямыми

x 1	у 1		z	,	x	у		z	.

2	2	4			2	3	4

3.6. Взаимное расположение двух прямых в пространстве

Под углом между двумя прямыми в пространстве понимается любой из двух смежных углов, которые образуют прямые, проведенные параллельно данным через какую-нибудь точку пространства 0 .

Угол находится из формулы

m1m2 n1n2

p1 p2

cos

s1 s2

(3.33)

m12 п12 p12

m22 n22 p22

Условие параллельности прямых:

L || L s1 || s

(3.34)

Условие перпендикулярности прямых:

L1 L2 s1 s2 s1 s2

0 m1m2

n1n2 p1 p2 0 .

(3.35)

П р и м е р 3.11. Найти величину угла между прямыми

x 4

у 1

z 5

х у 2z 8 0,

2х у

z 3 0.

Р е ш е н и е

Направляющий вектор первой прямой s1 3;1; 2 . Находим направ-


			i		j	k
												2 1; 5; 3 .
ляющий вектор s 2			1	1		2	i 5 j 3k , т. е.				s	2 1; 5; 3 .
			2	1		1

	3 1 1 5 2 3
										10
cos								10	, arccos	10			85 .
										35

		9 1 4 1 25 9						35

П р и м е р 3.12. Установить взаимное расположение прямых:

z 1

х 5 8t,

а)

y 4

6t, t R ;

z 3

б)

у 1

z 2

x 4

у 3

z 1

Р е ш е н и е
а) Направляющие векторы прямых		1 4; 3; 2		,		2 8; 6; 4 . Так
	s				s
как координаты этих векторов пропорциональны			4		3		2	, то данные
					6
			8				4

прямые параллельны или совпадают. Возьмем на первой прямой какую-нибудь
точку, например точку			M 0	2; 0; 1 . Подставим ее координаты в уравнение
второй прямой
				2 5 8t,

				0 4 6t,

				1 3 4t.
Получаем t	3	из	первого уравнения, t		2	– из второго, t 1 – из
Получаем t		из	первого уравнения, t			– из второго, t 1 – из
8					3

третьего. Так как полученные значения различны, то это означает, что точка M 0 2; 0; 1 не принадлежит второй прямой. Прямые не совпадают, значит

они параллельны;

б) Координаты направляющих векторов s1 2; 3;1 и s 2 3; 2; 4 данных прямых не пропорциональны. Следовательно, прямые либо пересека-

ются, либо являются скрещивающимися. Выпишем координаты точек, через
которые проходят данные прямые: М1 0;1; 2						и	М 2 4; 3;1		. Проверим
условие принадлежности двух прямых одной плоскости
	x2 x1	y2 y1	z2 z1		4	4 3
	x2 x1	y2 y1	z2 z1		4	4 3
	m1	n1	p1	= 0,	2	3	1	115 0 .
	m2	n2	p2		3	2	4

Следовательно, данные прямые являются скрещивающимися.

3.6.1Задачи для самостоятельного решения

1.Найти величину острого угла между прямыми

а)

б)

у 1

z 1

х 4

z 1

;

x y 2 0,

x y z 1 0,

y z 6 0

x y 3z 1 0.

2. Установить взаимное расположение прямых:

		0,	x 18t,

2x 3y 3z 9			и y 10t,	t R;
а)	2 y z 3
x		0
			x 3 2t,

б)

у 30

z 2,5

х 1

y 7

z 4

Даны прямые

х 1

у 1

z 3

х 4

z 1

. При каком значе-

нии параметра m прямые: а) перпендикулярны; б) параллельны?

3.7. Взаимное расположение прямой и плоскости

Величина угла

между прямой (L)

х х0

у y0

z z0

и плоскостью

Q Ax By Cz D 0 определяется по формуле

sin

Am Bn Cp

(3.36)

m2 n2 p2

A2 B2 C 2

Условие параллельности прямой и плоскости:

Q Am Bn Cp 0.

(3.37)

Условие перпендикулярности прямой и плоскости:

L Q

(3.38)

Координаты точки пересечения прямой и плоскости находятся из решения

системы уравнений:

x x0 mt, y y0 nt,

z z0 pt,

t R,

(3.39)

Ax By Cz D 0.

П р и м е р 3.13. Найти величину угла между прямой

х 3

у 6

z 7

и плоскостью 4х 2у 2z 3 0.

Р е ш е н и е

Воспользуемся формулой (3.36):

sin

4 1 2 1 2 2

, следовательно, .

1 1 4 16 4 4

П р и м е р 3.14. Установить взаимное расположение прямой и плоскости:

а)

б)

x 2 4t,

y t, t R и 5x 6y 2z 10 0;

z 3 2t,

х 1	у 2		z 4	и 3x y 4z 15 0 .
	1
3		2

Р е ш е н и е
а) Имеем		4;1; 2 ,		5; 6; 2			. Прямая не перпендикулярна плос-
а) Имеем	s	4;1; 2 ,	n	5; 6; 2			. Прямая не перпендикулярна плос-

кости, так как координаты векторов s					и n не пропорциональны
				4	1			2	.
				4		6			.
			5			6	2

Условие параллельности прямой и плоскости (3.37) также не выполняется

Am Bn Cp 5 4 6 1 2 2 20 6 4 22 0 .

Следовательно, прямая пересекает плоскость. Параметрические уравнения прямой подставим в уравнение плоскости и найдем точку пересечения

					2		3		4	1
				4		;		;			.
				4		;		;			.
					5		5			5
б) Имеем		3; 1; 2 ,		3;1; 4					. Условие (3.37) параллельности пря-
б) Имеем	s	3; 1; 2 ,	n	3;1; 4					. Условие (3.37) параллельности пря-

мой и плоскости выполняется

Am Bn Cp 3 3 1 1 4 2 0.

Следовательно, данная прямая параллельна плоскости или принадлежит ей. Возьмем любую точку М 0 прямой, например М 0 1; 2; 4 . Подставим

ее координаты в уравнение плоскости

Aх0 Bу0 Cz0 D 3 1 2 4 4 15 0.

Таким образом, прямая принадлежит плоскости.

3.7.1 Задачи для самостоятельного решения

1. Установить взаимное расположение прямой L и плоскости

Q :

x y 4z 6 0,

L , 3x y 6z 12 0

Q ;

а)

2x y z 3 0.

б)

у 13

z 7

L , 5x z 4 Q .

2. Составить уравнение плоскости, проходящей через точку M 0 1; 2; 5

перпендикулярно прямой

х 1

у 4

3. Найти угол между прямой

х 1

у 3

z 4

и плоскостью z 3 0 .

4. При каком значении параметра

m прямая

х 1

у 2

параллель-

на (перпендикулярна) плоскости x 4y 6z 5 0 ?

3.8. Кривые второго порядка

Окружностью называется множество точек плоскости, равноудаленных от данной точки, называемой центром.

Уравнение окружности радиуса R c центром в точке М 0 х0 ; у0 :

х х	2 у у	0	2	R2 .	(3.40)
0		0

Если центр окружности совпадает с точкой О (0; 0), то ее уравнение записывается в виде x2 y2 R2 .

Эллипсом называется множество точек плоскости, сумма расстояний от которых до двух данных точек, называемых фокусами, есть величина постоянная (обозначаемая через 2а), большая, чем расстояние между фокусами.

Если оси координат расположены так, что ось Ох проходит через точки F1 и F2 , а точка О(0; 0) совпадает с серединой отрезка F1F2 (рис. 10), то простей-

шее (каноническое) уравнение эллипса с центром в начале координат

x2	y 2	1.	(3.41)
a2	b2	1.	(3.41)
a2	b2
	у	b

a -а

-b

Рис. 10

Здесь а –

большая

полуось, b

–

малая

полуось

а b ,

точки

с; 0 , F c; 0

– фокусы эллипса, c

b2 .

2 b2

Эксцентриситет эллипса ε

Уравнения директрис эллипса x

Замечание. Каноническое уравнение эллипса с центром в начале новой

системы координат O x y :

x х0 2

y у0

(3.42)

Оси O x y параллельны и одинаково направлены соответственно осям Ох

и Оу. Начало новой системы координат в точке O (x0 ; y0 ) , где

x0 и y0

– коор-

динаты точки O в старой системе координат. Единица масштаба в обеих сис-

темах одна и та же.

Гиперболой называется множество точек плоскости, абсолютная величина

разности расстояний от которых до двух данных точек, называемых фокусами,

есть величина постоянная (обозначаемая через 2а), меньшая, чем расстояние

между фокусами.

Если ось Ох проходит через точки F1

и F2 , а точка О (0; 0) – середина от-

резка F1F2 , то простейшее (каноническое) уравнение гиперболы с центром в на-

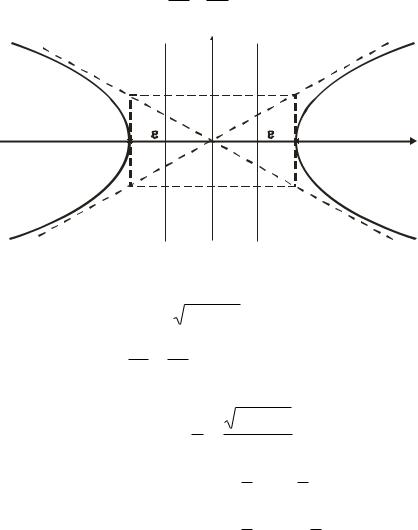
чале координат (рис. 11):

х2

у 2

(3.43)

а2

. b

- а- а .

. а

-b

Рис. 11

Здесь а – действительная полуось,

b – мнимая полуось, точки F1 c; 0 ,

F c; 0 – фокусы гиперболы, c

b2 .

Отметим, что уравнение

х2

у2

1 так же является уравнением гипербо-

а2

лы, но действительной осью этой гиперболы служит отрезок оси Оу длиной 2b .

Эксцентриситет гиперболы ε

а2 b2

Уравнения директрис гиперболы x a

x a .

Уравнения асимптот гиперболы у b

х ,

у b

х .

Замечание. Каноническое уравнение гиперболы с центром в начале новой

системы координат O x y :

x х

y у

(3.44)

Оси O x y параллельны и одинаково направлены соответственно осям Ох и Оу. Начало новой системы координат в точке O (x0 ; y0 ) , где x0 и y0 – коор-

динаты точки O в старой системе координат. Единица масштаба в обеих системах одинакова.

Параболой называется множество точек плоскости, равноотстоящих от данной точки, называемой фокусом, и данной прямой, называемой директрисой.

Если парабола симметрична относительно оси Ох и проходит через начало координат, то простейшее (каноническое) уравнение параболы с вершиной в начале координат (рис. 12):

	у2 2 рх р 0 .			(3.45)
p
Точка F	; 0 – фокус параболы.
Точка F	; 0 – фокус параболы.
2
Эксцентриситет параболы ε 1.
Уравнение директрисы параболы х		р	.
Уравнение директрисы параболы х		2	.
		2

		. . .
	р	0	.	х
-			F
	2

Рис. 12

Если парабола симметрична относительно оси Оу и проходит через начало координат, то простейшее (каноническое) уравнение параболы x2 2 py .

Замечание. Каноническое уравнение параболы с центром в начале новой

системы координат O x y :
у у0 2 2 р х х0 .	(3.46)
Оси O x y параллельны и одинаково направлены соответственно осям Ох
и Оу. Начало новой системы координат в точке O (x0 ; y0 ) , где	x0 и y0 – коор-

динаты точки O в старой системе координат. Единица масштаба в обеих системах одна и та же.

Эллипс, гипербола, парабола обладают общим свойством: отношение расстояния r произвольной точки кривой до фокуса к расстоянию d этой точки до

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 109 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
20.02.20163.15 Mб315Учебник КОМПЛЕКСНЫЙ АНАЛИЗ 1часть.doc
#
17.11.201981.16 Кб10Учебник по 2ин.яз для ЗФО (1).docx
#
20.02.2016876.25 Кб2467Учебник по Истории.pdf
#
14.08.2019803.33 Кб49Учебник по переводу 3 курс.doc
#
14.11.20192.4 Mб70Учебник.Основы растениеводства.doc
#
20.02.20162.05 Mб26УЧЕБНО-МЕТОДИЧ. ПОСОБИЕ ПО ВМ_1.pdf
#
20.02.201611.55 Mб204Учебно-методическое пособие (лекционная часть).doc
#
20.02.20162.31 Mб25Учебно-методическое пособие ВМ 2часть.pdf
#
20.02.20161.86 Mб29Учебно-прктич. пособие по матем.pdf
#
07.11.20182.12 Mб134Учебное пособие по охране труда.doc
#
15.11.2018458.75 Кб3учебное пособие по дел док 1 (книга).doc