УЧЕБНО-МЕТОДИЧ. ПОСОБИЕ ПО ВМ_1

4.а) x1 2, x2 2; б) x1 1,5 0,5t, x2 0,5 0,5t, x3 t, t R ;

в) x1 8, x2 4, x3 4 ; г) система несовместна.

5.а) x1 4, x2 0, x3 2; б) x1 1, x2 2, x3 2 ; в) система несовместна.

7. а) x1 34 t, x2 t, t R ; б) x1 t, x2 t, x3 t, t R ;

в) x1 0, x2 0, x3 0 ; г) x1 1,4t, x2 0,2t, x3 t, t R ; д) x1 0, x2 0, x3 0 .

52

Тема 2. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ

2.1. Векторы на плоскости и в пространстве. Скалярное произведение векторов

Вектором называется направленный отрезок AB , где точка А – начало вектора, точка В – конец вектора. Если начало и конец вектора в явном виде не

указаны, то вектор будем обозначать а, х и т. д.

Вектор, у которого начало и конец совпадают, называется нулевым векто-

ром и обозначается 0 .

Длиной (модулем) вектора AB называется число, равное длине отрезка АВ и обозначается АВ .

Вектор, длина которого равна единице, называется единичным или ортом. Векторы, параллельные одной и той же прямой, называются коллинеарными.

Два вектора а и b называются равными а b , если они имеют одинако-

С – вершина АВСD (рис. 2).

Разностью двух векторов a и b называется вектор a b и обозначается a b (рис. 3).

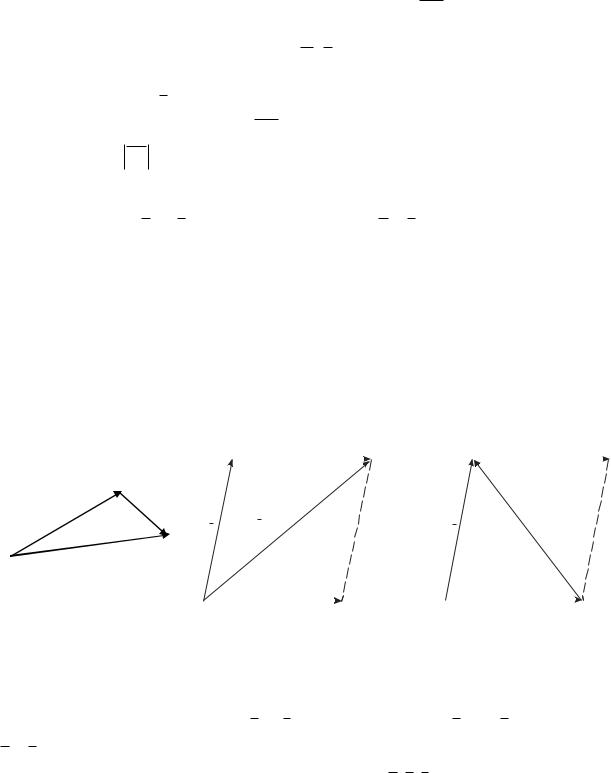
На рис. 4 показано сложение трех векторов a, b, с .

53

Базисом на плоскости называется упорядоченная пара любых неколлинеарных векторов этой плоскости.

Если e1, e2 – базис на плоскости, то любой вектор а этой плоскости един-

Базисом в пространстве называется упорядоченная тройка любых некомпланарных векторов.

Если e1, e2 , e3 – базис в пространстве, то любой вектор а единственным образом представляется в виде линейной комбинации векторов e1, e2 , e3 , т. е. a хe1 ye2 ze3 . Это равенство называется разложением вектора а по базису в пространстве. Числа x, y, z называют координатами вектора а в базисе

Линейные операции над векторами

Пусть а х1; у1; z1 , b x2 ; y2 ; z2 , R .

54

Два вектора, заданные координатами в фиксированном базисе, равны тогда и только тогда, когда равны их соответствующие координаты.

При умножении вектора на число все его координаты умножаются на это

число: a ( x1 ; y1 ; z1 ) .

При сложении двух векторов складываются их соответствующие коорди-

Декартовой прямоугольной системой координат в пространстве называ-

ется совокупность трех упорядоченных взаимно перпендикулярных осей координат Ох, Оу, Oz с общим началом в точке О. Орты координатных осей Ох, Оу,

Oz обозначают i, j, k соответственно. Векторы i, j, k образуют декартовый прямоугольный базис в пространстве.

Координаты вектора а в базисе i, j, k называют декартовыми прямо-

угольными координатами вектора а и записывают а х; у; z .

Координатами точки М в заданной системе координат называют координаты ее радиус-вектора ОМ . В этом случае пишут М х; у; z или M x; y; z .

Первая координата называется абсциссой, вторая – ординатой, третья – аппли-

катой.

Базис называется ортонормированным, если базисные векторы попарно ортогональны и длина каждого из них равна единице.

Длина вектора a (x; y; z) , заданного своими координатами в ортонормированном базисе, определяется равенством

ванными вектором a с положительными направлениями осей Ох, Оу и Оz соответственно. Косинусы этих углов называются направляющими косинусами вектора а и определяются по формулам:

Направляющие косинусы связаны соотношением

cos2 cos2 cos2 1

55

Скалярным произведением двух векторов a и b называется число, обозначаемое ab , равное произведению длин этих векторов на косинус угла между

a 2 a a a a cos 0 a 2 ;

5) a 2 a .

Из определения скалярного произведения следует, что

Ненулевые векторы a и b перпендикулярны (ортогональны) тогда и только тогда, когда их скалярное произведение равно нулю:

56

Найдем координаты вектора а :

а2 4; 4; 4 3 3;1; 6 1; 5; 2 8; 8; 8 9; 3;18 1; 5; 2

=8 9 1; 8 3 5; 8 18 2 18;10; 24 .

Тогда длина вектора а находится по формуле (2.1):

а182 102 24 2 324 100 576 1000 31,6.

Пр и м е р 2.2. Упростить выражение a b a b .

Р е ш е н и е Воспользуемся свойствами скалярного произведения:

a b a b a a a b b a b b a a cos 0 а b a b bb cos 0 a 2 b 2

=a2 b2 .

Пр и м е р 2.3. Определить, перпендикулярны ли векторы а и b , если a 3i 4 j k , b 4i 5k .

Р е ш е н и е

Векторы а и b имеют координаты: a 3; 4;1 , b 4; 0; 5 . Вычислим по формуле (2.4) скалярное произведение

а b 3 4 4 0 1 5 7 0 .

Следовательно, векторы a и b не перпендикулярны, так как не выполняется условие перпендикулярности (2.6).

П р и м е р 2.4. Найти координаты вектора b , коллинеарного вектору a i 2 j 3k при условии a b 14 .

57

Р е ш е н и е. Из условия коллинеарности векторов (2.7) следует, что суще-