1) Лінійні і нелінійні задачі:

- лінійні - в лінійних задачах цільова функція та система обмежень не повинні містити інших, ніж одиниця або нуль степенів невідомих та добутків невідомих. Для розв’язання цих задач застосовується симплексний метод лінійного програмування, який є універсальним для всіх лінійних задач;

- нелінійні– нелінійні задачі розв’язуються за допомогоюметодів нелінійного програмування.Універсального методу розв’язання нелінійних задач немає, але для окремих груп задач розроблені спеціальні методи, зокрема,методи опуклого програмування: градієнтний метод, метод штрафних функцій тощо. В задачахопуклого програмуванняцільова функція та система обмежень представленіопуклими (угнутими) функціями, причому обмеження повинні бутиоднотипними нерівностями або рівняннями. Частинним випадком опуклого програмування єквадратичне програмування. До задач квадратичного програмування відносяться задачі, які маютьлінійні обмеження і цільову функцію, що складає сумулінійної таквадратичної форм. Для розв’язаннянелінійних задач з неперервними диференційованими функціями та лінійними обмеженнямизастосовуєтьсяметод множників Лагранжа.

2) Дискретні та неперервні задачі:

- дискретні - в дискретних задачах усі або деякі невідомі в розв’язку повинні набувати дискретних або цілочислових величин. Такі задачі розв’язуються за допомогою методів дискретного програмування. Частинним випадком дискретного програмування є цілочислове програмування, задачі якого розв’язуються за допомогою методу відтинання Гоморі, методу розгалужень і меж тощо;

- неперервні - в неперервних задачах невідомі в розв’язку можуть набувати будь-яких значень в деяких інтервалах числової осі;

3) Детерміновані та стохастичні (ймовірностні) задачі:

- детерміновані - детерміновані задачі не повинні містити випадкових невідомих і функцій, які підлягають певним статистичним розподілам;

- стохастичні (ймовірностні) - стохастичні задачі містять випадкові параметри і розв’язуються за допомогоюметодів стохастичного програмування, які базуються на математичному апараті теорії ймовірностей;

4) Статичні (однокрокові) та динамічні (багатокрокові) задачі:

- статичні (однокрокові) - в статичних задачах всі компоненти вектора оптимального розв’язку визначаються одночасно за один кінцевий крок алгоритму;

- динамічні (багатокрокові) - в динамічних задачах оптимальні значення множини невідомих визначаються поетапно крок за кроком. Істотну роль в цих задачах відіграє фактор часу або певна послідовність операцій. Такі задачі розв’язуються за допомогою методівдинамічного програмування.

Окремими розділами МП є теорія ігор та імітаційне моделювання.

Слід зауважити, що одна і та ж задача МП може одночасно мати властивості всіх наведених вище класів задач.

Найбільш простими і тому найбільш поширеними є лінійні неперервні детерміновані статичні задачі, які розв’язуються за допомогоюсимплексного методу лінійного програмування (ЛП).

ЗМ 2. Лінійне програмування

Загальною задачею лінійного програмування (ЗЗЛП) є задача на знаходження екстремуму лінійної цільової функція при лінійній системі обмежень, яка у розширеній формі математично формулюється так: знайти вектор невідомих х = (х₁, х₂, ..., х_j, ..., х_n) , при якому цільова функція Z досягає екстремуму

Z_ext = с₁х₁ + с₂х₂ + ... + c_jx_j + ... + c_nx_n

при обмеженнях:

а₂₁х₁ + а₂₂х₂ + ... + а_2jx_j + ... + а_2nx_n { > = < } b₂

..........

а_i1х₁ + а_i2х₂ + ... + а_ijx_j + ... + а_inx_n { > = < } b_i

..........

а_m1х₁ + а_m2х₂ + ... + а_mjx_j + ... + а_mnx_n { > = < } b_m

або в скороченій формі:

_n __

Z_ext = ∑ c_j x_j j(1,n)

^j=1

при обмеженнях:

_n ___

1) ∑ a_ij x_j { > = < } b_i i(1,m)

^j=1

2) x_j >= 0

Запис задачі у векторно-матричній формі буде такий : знайти

Z_ext = СХ

при обмеженнях:

1) АХ { > = < } В

2) Х >= 0

де Х = (х₁, х₂, ..., х_j, ..., х_n) - вектор або матриця-рядок невідомих задачі;

С = (с₁, с₂, ..., с_j, ..., с_n) - вектор або матриця-рядок коефіцієнтів лінійної

форми або оцінок невідомих задачі;

А = (a_ij ) _nm - матриця розміром n х m коефіцієнтів при невідомих в

обмеженнях задачі або матриця умов задачі, де n – кількість колонок,

а m –кількість рядків;

B = (b₁, b₂, ..., b_i, ..., b_m) - вектор або матриця-колонка обсягів обмежень задачі.

Завдання 1. Графічний метод.

Теоретична частина. В задачах лінійного програмування потрібно

знайти

_n

Z _ext = ∑ c_j x_j j(1,n)

^j=1

при обмеженнях:

_n

1) ∑ a_ij x_j { ≥ = ≤ } b_i i(1,m)

^j=1

2) x_j ≥ 0.

При кількості невідомих n = 2, або дляn > 2, якщо при зведенні системи нерівностей до системи рівнянь шляхом введення додаткових змінних кількість зміннихnна2 більша числа обмеженьm,тобтоn – m = 2, задача розв'язуєтьсяграфічним методомза таким алгоритмом:

1. В системі координат Х₁ОХ₂ (перший квадрант системи координат двомірного простору, що обумовлено умовою невід'ємності змінних) представимо обмеження-нерівності а_і1х₁ + а_і2х₂ {≥} b_і, кожне з яких поділяє систему координат на дві напівплощини, межами яких є прямі, визначені рівняннями

а_і1х₁ + а_і2х₂ = b_і.

2. Для того, щоб визначити, для якої напівплощини виконується обмеження, потрібно взяти координати точок в першій і другій напівплощинах і перевірити, в якій із напівплощин виконується обмеження-нерівність.

3. Напівплощини, в яких виконуються обмеження, при перетині в системі координат Х₁ОХ₂ утворюють спільну частину, яка називається багатокутником розв'язків. Кожна точка цього багатокутника є розв'язком задачі, тому що в ній виконуються всі обмеження. Такий розв'язок називається допустимим.

4. Будуємо вектор N з координатами точок О (0,0) та N (с₁, с₂), який задає напрям зміни значення цільової функції (для задач максимізації в напрямку вектору, для задач мінімізації - в протилежному).

5. Будуємо пряму с₁х₁ + с₂х₂ =const, перпендикулярну до вектора N, яка називається лінією рівня цільової функції.

6. Пересуваємо пряму с₁х₁ + с₂х₂ =const паралельно саму до себе до тих пір, поки вона не торкнеться крайньої точки (вершини) багатокутника допустимих розв'язків. В цій точці цільова функція досягає екстремального значення. При розв"язанні задачі на максимум цільової функції екстремальна точка знаходиться якнайдалі від початку координат, а на мінімум – якнайближче.

7. Визначаємо координати точки, в якій цільова функція досягає екстремального значення, для чого розв'язуємо систему рівнянь двох прямих, перетином яких є оптимальна точка. Отримані координати точки є оптимальним розв'язком задачі.

8. Обчислюємо значення цільової функції і перевіряємо виконання обмежень.

К

онтрольні питання

1. Що називається математичною моделлю економічної задачі?

2. Які задачі лінійного програмування можна розв'язати графічним методом?

3. Що означають координати будь-якої точки багатокутника допустимих

розв'язків задачі?

4. В якій точці багатокутника допустимих розв'язків цільова функція досягає

екстремального значення?

5. Як умовам повинна задовольняти оптимальна точка при розв"язанні задачі на

максимум цільової функції?

6. Як умовам повинна задовольняти оптимальна точка при розв"язанні задачі

на мінімум цільової функції?

7. В якому випадку задача лінійного програмування має множину оптимальних

розв’язків?

Приклад 1.1. Для виробництва зерна озимої пшениці та кукурудзи виділено 600 га ріллі та 32000 люд.-год. Затрати праці та урожайність (в розрахунку на 1 га) такі:

Показник	Пшениця	Кукурудза
1. Затрати праці, люд.-год.	40	80
2. Урожайність, ц	50	70

Посівна площа кукурудзи повинна бути не менша 100 га. Знайти посівні площі озимої пшениці та кукурудзи, які б забезпечили максимум виробництва зерна.

Розв'язання. Для побудови економіко-математичної моделі позначимо:

х₁ – посівна площа озимої пшениці, га

х₂ – посівна площа кукурудзи на зерно, га

Z – обсяг виробництва зерна, ц.

Тоді, умови задачі в математичній формі можна записати так:

1. Умова використання ріллі: посівні площі озимої пшениці та кукурудзи не повинні перевищувати наявної площі ріллі: х₁ + х₂ 600

2. Умова використання трудових ресурсів: затрати праці на вирощування сільськогосподарських культур не повинні перевищувати наявного обсягу трудових ресурсів: 40х₁+ 80х₂32000

3. Умова обмеження площі кукурудзи: посівна площа кукурудзи на зерно повинна бути не менше 100 га:х₂100

4. Умова невід'ємності змінних: посівні площі сільськогосподарських культур не можуть бути від'ємними числами: х₁0;х₂0.

Кінцеву мету задачі – отримання максимуму зерна - запишемо як функцію двох змінних х₁ і х₂: Z_mаx= 50х₁ + 70х₂

Нерівності на графіку являють собою напівплощини, межами яких є прямі лінії, визначені рівняннями відповідно: х₁+х₂ = 600 (L₁); 40х₁+80х₂ = 32000 (L₂) та х₂ = 100 (L₃). Побудуємо ці прямі в додатному квадранті системі координат Х₁ОХ₂, оскільки х₁0;х₂0. Для побудови на графіку будь-якої прямої знайдемо принаймні дві точки, які їй належать, наприклад, для рівняннях₁ + х₂ =600: якщо х₁ = 0, то х₂ = 600, а якщо х₂ = 0, то х₁ = 600.Через точки (0;600) та (600;0) проведемо пряму L₁. Аналогічно побудуємо прямі L₂ та L₃ (рис.1.)

Оптимальний розв'язок знаходимо, визначаючи напрямок зростання цільової функції Z_max= 50x₁ + 70x_2. Для цього побудуємо вектор N з координатами точок О (0;0) - початок координат - та N (50;70) - оцінки невідомих цільової функції. В точці О проведемо до вектора N перпендикуляр, який відповідає лінії рівня цільової функції Z=0.

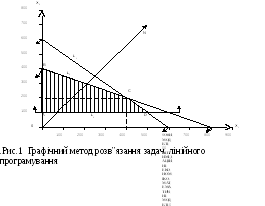
Значення Z зростає в напрямку вектора N (див. рис. 1), тому пряму Z=0 пересуваємо паралельно саму до себе в напрямку вектора N доти, поки вона не торкнеться крайньої верхньої точки (вершини) багатокутника допустимих розв'язків АВСD. Оптимальним розв"язком задачі будуть координати точки С, яка одночасно належить багатокутнику допустимих розв'язків АВСD і прямій рівня цільової функції Z_max =50х₁+70х₂, а також знаходиться якнайдалі від початку координат (задач розв"язується на максимум цільової функції). На рис.1 видно, що точка С є точкою перетину прямих L₁ і L₂. Отже, щоб визначити х₁ і х₂, потрібно розв'язати систему рівнянь:

х₁+х₂=600

40х₁+80х₂=32000

Розв'язок системи рівнянь: х₁=400; х₂=200.

Висновки.Для отримання максимальної кількості зерна в обсязі 34000 ц

(Z_max =50400+70200=34000) площа озимої пшениці повинна дорівнювати 400 га, (х₁=400), а кукурудзи – 200 га (х₂=200). При цьому повністю використані площа ріллі (400+200=600) та трудові ресурси (40400+80200=32000). Площа кукурудзи перевищує задану на 100 га (200-100=100).

Задачі для самостійного розв'язування

Задача 1.1. В господарстві для вирощування кукурудзи на зерно та ячменю виділено 400 га ріллі та 12000 люд.-год. Затрати праці на 1 га та урожайність сільськогосподарських культур наведені в табл.1.1.

Знайти посівні площі сільськогосподарських культур з метою отримання максимальної кількості фуражного зерна, якщо відомо, що площа кукурудзи на зерно повинна бути не менше 50 га.

Таблиця 1.1

Сільськогосподарська культура	Варіант *)	Затрати праці на 1 га, люд.-год.	Урожайність, ц з 1га
Кукурудза на зерно	0	60	60
	1	50	55
	2	40	50
	3	60	60
	4	50	55
	5	40	50
	6	60	60
	7	50	55
	8	40	50
	9	60	60
Ячмінь	0	30	50
	1	25	40
	2	20	30
	3	30	55
	4	25	45
	5	20	35
	6	30	40
	7	25	35
	8	20	30
	9	30	40

^*) Варіант технології вирощування кукурудзи на зерно вибирається за передостанньою цифрою шифру Р, а ячменю – за кінцевою К.

Задача 1.2. Знайти посівні площі зернових фуражних культур з метою мінімізації затрат праці на їх вирощування. Вихід поживних речовин і затрати праці на виробництво кормів (в розрахунку на 1 га) такі:

Показник	Кукурудза на зерно	Горох
1. Вихід кормових одиниць, ц	70	40
2. Вихід перетравного протеїну,ц	4	6
3. Затрати праці, люд.-год.	40	30

Планові завдання виробництва кормів та площа ріллі наведені в табл. 1.2.

Таблиця 1.2

Варіант (за передостанньою цифрою шифру Р)	Планові завдання виробництва, ц		Площа ріллі, га
	кормових одиниць	перетравного протеїну
0	14000	1200+10К	500
1	15000	1300+10К	510
2	16000	1400+10К	520
3	17000	1500+10К	530
4	18000	1700+10К	540
5	19000	1800+10К	550
6	20000	1900+10К	560
7	21000	2000+10К	570
8	22000	2100+10К	580
9	23000	2200+10К	590