381

1.2 Проекції відрізків прямих ліній

Положення прямої лінії у просторі визначається двома її кінцевими точками або однією точкою і напрямком S прямої, що проходить через цю точку. Проекція відрізка прямої – пряма лінія. Визначником відрізка прямої є дві точки. Умовний запис визначника прямої: l (А, В). На комплексному кресленні пряму визначають двома проекціями: АВ (А1В1; А2В2 ) або l (l1, l2 ).

Пряма лінія в просторі може займати загальне і окреме положення. Пряма загального положення – така пряма, яка не паралельна і не перпен-

дикулярна до жодної площини проекцій. Координати її поточних точок змінні. Вона має три сліди. Кожна з проекцій прямої загального положення менше її натуральної величини.

Прямі окремого положення поділяються на:

-прямі рівня;

-проеціюючі прямі.

Пряма рівня – така пряма, яка паралельна хоча б одній площині проек-

цій або належить їй. Вона не має слідів на площині проекцій, до якої вона паралельна, і проеціюється на цю площину в натуральну величину (НВ).

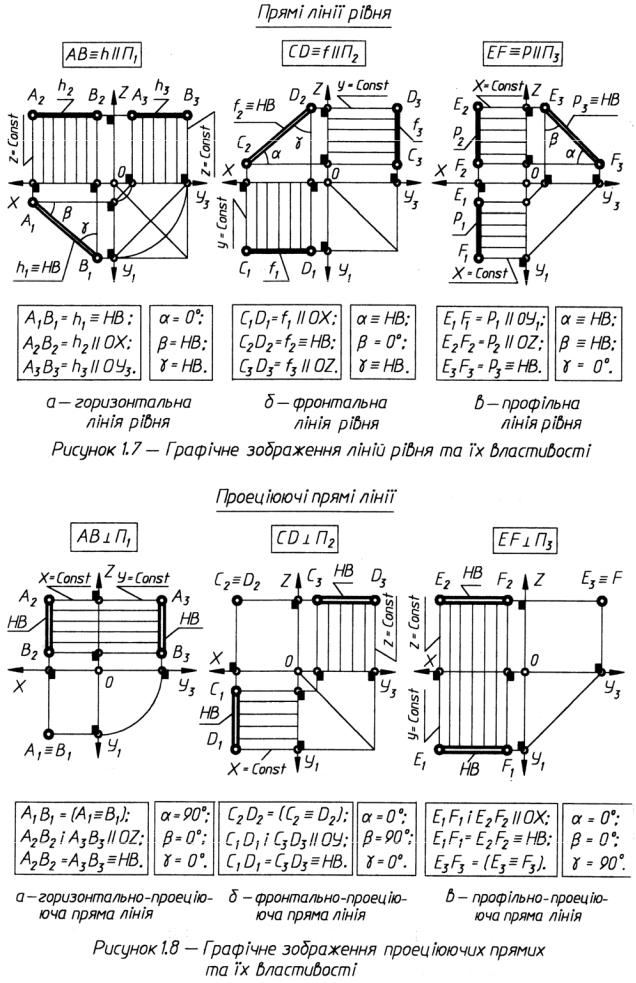
Відомі такі прямі рівня та їх позначення і властивості:

горизонтальна пряма рівня – h(h1, h2, h3)║П1; h1≡НВ; h2║0х; h3║0у;

γ≡ НВ; β≡ НВ; Z= Const; Рис. 1.7 а;

-фронтальна пряма рівня – f(f1, f2, f3)║П2; f1║0х; f2≡НВ; f3║0z; α≡НВ; γ

≡ НВ; У= Const; Рис. 1.7 б;

-профільна пряма рівня – p(p1; p2; p3)║П3; p1║0у; p2║0Z; p3≡НВ; α≡НВ;

β ≡ НВ; X= Const; Рис. 1.7 в.

Проеціююча пряма – така пряма, яка перпендикулярна до однієї площини проекцій та її проекція на цій площині перетворюється в точку, у котрої тотожно збігаються дві кінцеві точки відрізка прямої, а до інших двох площин проекцій вона паралельна, тому є натуральною величиною.

Відомі такі проеціюючі прямі та їх позначення і властивості:

- горизонтально-проеціююча пряма – АВ П1; АВ║П2 і║П3; А1≡В1;

А2В2= А3В3 ≡ НВ; Х = Соnst; У = Сonst; Рис. 1.8 а;

31

-фронтально-проеціююча пряма – АВ П2; АВ║П3 і П1; А1В1=А3В3≡НВ;

X= Const; Z= Const; Рис. 1.8 б;

-профільно-проеціююча пряма – АВ П3; АВ║П1 і П2; А1В1=А2В2≡НВ;

Z= Const; У= Const; Рис. 1.8 в.

Для завдання відрізка прямої в просторі достатньо задати дві її точки А і В. Утворення комплексного креслення прямої аналогічно утворенню комп-

лексного креслення точки. Для відрізку прямої лінії потрібно будувати за коор-

динатами вже дві точки, а потім – з'єднати їх між собою. (рис. 1.9 а).

Точки перетину прямої з площинами проекцій називаються слідами прямої і визначаються як точки прямої, одна з координат яких дорівнює нулю

(рис. 1.9 а).

Для побудови слідів прямої лінії існує таке правило:

–для знаходження горизонтального сліду прямої (М) необхідно її фронтальну проекцію продовжити до перетину із віссю Ох у точки М2 і від М2 провести лінію зв'язку до перетину її із продовженням горизонтальної проекції прямої в точке М1 ≡ М;

–для знаходження фронтального сліду прямої (N) необхідно її гоизонтальну проекцію продовжити до перетину із віссю Ох у точки N1 і від N1 провести лінію зв'язку до перетину її із продовженням фронтальної проекції прямої

вточке N2 ≡ N.

Якщо перетин буде на П1, то слід має назву горизонтальний і позначаєть-

ся М ≡ М1, а точка М2 – фронтальна проекція горизонтального сліду.

Якщо перетин буде на П2, то слід має назву фронтальний і позначається

N ≡ N2, а точка N1 – горизонтальна проекція фронтального сліду.

НВ прямих особистого положення очевидна (див. рис. 1.7 та 1.8). Натуральну величину відрізка прямої загального положення визначають згідно пра-

вила прямокутного трикутника (рис. 1.9 а) довжиною гіпотенузи прямокут-

ного трикутника, побудованого на одній із проекцій, як на катеті. Другий катет трикутника дорівнює різниці відстаней кінців відрізка від тієї площини проек-

33

цій, на якій взято перший катет.

Кут між натуральною величиною відрізка прямої та її проекцією на горизонтальну площину є кутом нахилу прямої до площини П1, умовно позначається як α.

Кут між натуральною величиною відрізка прямої та її проекцією на фронтальну площину є кутом нахилу прямої до площини П2 , умовно позначається як .

Кут між натуральною величиною відрізка прямої та її проекцією на профільну площину є кутом нахилу прямої до площини П3, умовно позначається як γ.

Якщо пряма перпендикулярна до площини проекцій, то на цю площину вона проеціюється в точку.

Якщо відрізок прямої паралельний площині проекцій, то на цю площину він проеціюється в натуральну величину.

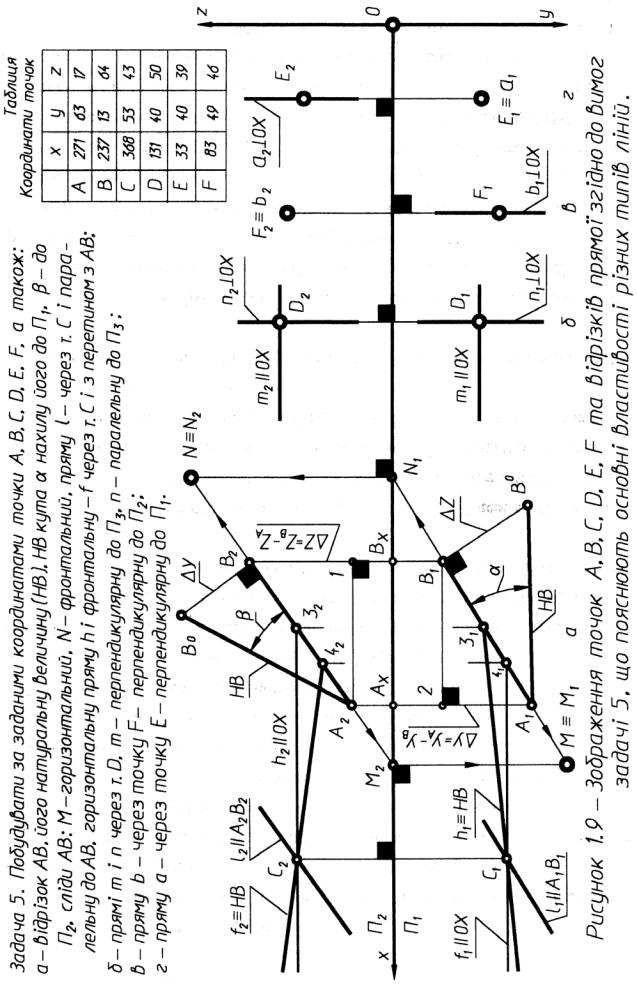
Задача 5. (Рис. 1.9) Побудувати за заданими координатами точки А, В, С, D, Е, F, а також:

а– відрізок АВ, його натуральну величину, НВ кута α нахилу його до П1,

– до П2, сліди відрізка АВ: М – горизонтальний, N – фронтальний, пряму l – через точку С і паралельно АВ, горизонтальну пряму h і фронтальну

– f через точку С із перетином з АВ;

б– прямі m і n через точку D, m – перпендикулярну до П3, n – паралельну

П3;

в– пряму b – через точку F – перпендикулярну до П2; г – пряму а – через точку Е – перпендикулярну до П1.

Розв’язання задачі 5:

Побудова відрізка прямої, його натуральної величини, слідів і кутів нахилу до площин проекцій

Спочатку за заданими координатами точок A, B, C, D, E, F треба побудува-

34

ти проекції точок в П1 і П2, потім будують:

- натуральну величину відрізка прямої АВ за допомогою правила прямокутного трикутника для прямої загального положення (рис. 1.9, а);

-натуральну величину α – кута нахилу відрізка АВ до П1 (визначають як кут між горизонтальною проекцією А1В1 та його натуральною величиною);

-натуральну величину β – кута нахилу відрізка АВ до П2 (визначають як кут між фронтальною проекцією А2В2 та його натуральною величиною);

-сліди відрізка АВ: М – горизонтальний, N – фронтальний.

Для визначення горизонтального сліду відрізка прямої АВ за її проекціями необхідно продовжити фронтальну проекцію А2В2 до перетину з віссю Ох, з точки М2 (фронтальної проекції горизонтального сліду) провести лінію зв'язку до перетину з продовженням горизонтальної проекції А1В1. Точка М1 є горизонтальною проекцією горизонтального сліду – вона збігається з самим слідом

М.

Для визначення фронтального сліду відрізка прямої АВ необхідно горизонтальну проекцію відрізка прямої А1В1 продовжити до осі Ох, з точки N1 (горизонтальної проекції фронтального сліду) провести лінію зв’язку до перетину з продовженням фронтальної проекції А2В2. Точка N2 є фронтальною проекцією фронтального сліду; вона збігається з самим слідом N.

- пряму l (l1, l2) – проводять через точку С паралельно до проекцій А1В1 і

А2В2;

- прямі рівня h (h1, h2) i f (f1, f2) – проводять через точку С так, щоб h i f перетинали побудований відрізок АВ; h2 проводять паралельно до осі Оx і до перетину з А2В2 в точці 32, потім за проекційною відповідністю визначають точку 31, далі через горизонтальні проекції точок С1 і 31 будують горизонтальну проекцію горизонталі – h1≡ НВ; f1 проводять паралельно до осі Оx до перетину з прямою А1В1 в точці 41, потім визначають 42, далі через фронтальні проекції точок С2 і 42 будують фронтальну проекцію фронталі f2 ≡ НВ;

- прямі n i m проводять через точку D таким чином, щоб n була паралельною до П3; m – перпендикулярна до П3. Пряма n – паралельна до П3, якщо її фронтальна проекція n2 паралельна осі Оz, а горизонтальна проекція n1 – паралельна осі Оу. Пряма m – перпендикулярна П3, якщо її горизонтальна і фронтальна проекції паралельни осі Оx.

35

Знайти натуральну величину (НВ) відрізка прямої АВ і кути нахилу до площини проекцій П1 і П2 ( рис. 1.9 а ).

Для визначення на кресленні натуральної величини відрізка прямої лінії з будь-якого кінця горизонтальної проекції цього відрізка, наприклад, з точки В1, проведемо пряму-промінь, перпендикулярну до цієї проекції, і на ній відкладемо відрізок В1Во, взятий із фронтальної проекції як різниця відстаней від проекцій В2 і А2 до осі ОХ, яка дорівнює Z = ZB - ZA. Відрізок А1В0 дорівнюватиме відрізку АВ ≡ НВ, а кут між А1 В0 і горизонтальною проекцією А1 В1 показуватиме нахил відрізка АВ до площини проекцій П1.

Для визначення кута β нахилу відрізка прямої АВ до площини проекцій П2 потрібно виконати подібні побудови на фронтальній проекції, наприклад, з точки В2, проведемо пряму-промінь, перпендикулярну до цієї проекції, і на ній відкладемо відрізок В2В°, взятий з горизонтальної проекції як різниця відстаней від проекцій А1 і В1 до осі Ох, яка дорівнює У= УА – УВ. Відрізок А2 В° дорівнюватиме відрізку АВ ≡ НВ, а кут β між А2В0 і фронтальною проекцією А2 В2 показуватиме нахил відрізка АВ до площини проекцій П2.

1.2.1 Взаємне положення прямих

Дві прямі у просторі можуть займати такі положення:

-бути паралельними (рис. 1.10 а);

-можуть перетинатися (рис. 1.10 б);

-бути мимобіжними (скрещивающимися) (рис. 1.10 в).

Дві прямі загального положення, а також дві фронталі і горизонталі паралельні між собою, якщо паралельні їхні однойменні проекції (рис. 1.10 а).

Уразі паралельності профільних прямих потрібно перевірити паралельність їх профільних проекцій на площині П3.

Дві прямі, що перетинаються, – це прямі, у яких перетинаються їхні проекції і точка перетину проекцій К лежить на одній лінії зв’язку (рис. 1.10 б).

Уразі перетину проекцій з профільною прямою необхідно проаналізувати

їїположення або перевірити на площині П3.

37

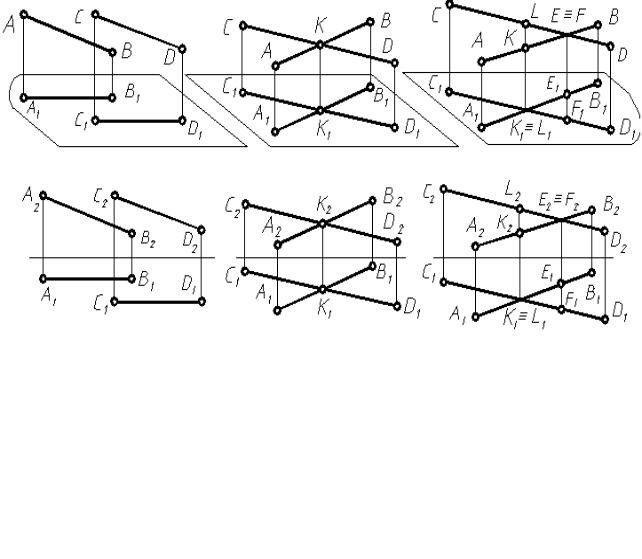
У мимобіжних прямих однойменні проекції також перетинаються, але точки перетину К, L і E, F не лежать на одній лінії зв'язку. Такі точки називають-

ся конкуруючими, тобто, К, L – горизонтально-конкуруючі та E, F – фрон-

тально-конкуруючі. За допомогою порівняння їх координат можна встановити

видимість прямих: видима та пряма, в якої конкуруюча точка має більшу

відповідну координату (рис. 1.10 в).

Здається, що на епюрі (рис. 1.10 в) проекції А2В2 і C2D2 перетинаються на площині П2, а А1В1 і C1D1 на – П1. Насправді мимобіжні прямі не перетинаються, а мають дві проекції точок, що збігаються Е2 ≡ F2, K1 ≡ L1 і ті, що не збігаються E1 ≡ F1, K2≡ L2. За координатами точок, що не збігаються, визначають які з точок, що збігаються, розташовані одна під або над другою на П1, а які – одна перед або за другою на П2. Точки F2 і L1 – видимі, E2 і K1 – невидимі.

Аналогічні висновки роблять і для прямих, яким належать зазначені точки. Коли YF > YE, то проекція C2D2, якій належить F2, проходить перед А2В2. А коли ZL> ZК, то пряма CD, якій належить точка L, проходить над АВ.

Рисунок 1.10 – Зображення взаємного положення двох відрізків прямих.

38

3* – Вправи для самостійної домашньої підготовки до практичного заняття з теми : “Проекції відрізків прямих ліній”

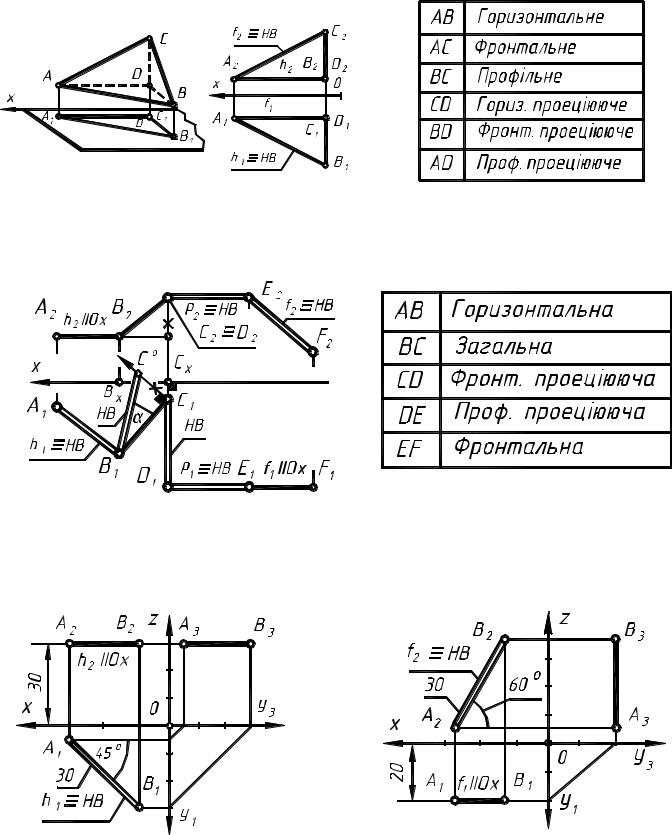
Вправа 3*.1 На епюрі літерами позначити проекції вершин піраміди та записати в таблицю положення ребер відносно площин проекцій.

Вправа 3*.2 На епюрі літерами позначити проекції кінців відрізків, що складають ламану лінію АВСDЕF, записати назву відрізків в таблицю та визначити натуральну величину відрізків.

Вправа 3*.3 Побудувати три проекції відрізка АВ = 30 мм таких прямих:

а) горизонтальної прямої на відстані 30 мм від площини П1 під кутом 45° до площини П2 (рис. а);

б) фронтальної прямої на відстані 20 мм від площини П2 під кутом 60° до площини П1 (рис. б).

39

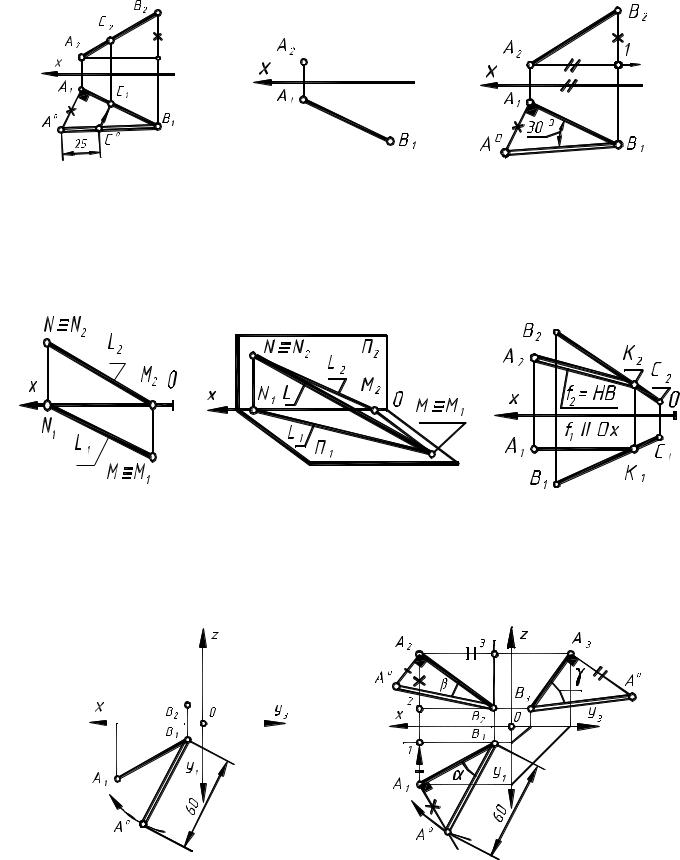
4*– Вправи для виконання в аудиторії на практичному занятті з теми: “Проекції відрізків прямих ліній” Вправа 4*.1 Побудувати на проекціях відрізка АВ проекції точки С, що розта-

шовані від точки А на відстані 25 мм (див. а).

а б – завдання: для вправи 4*.2; в – кінцеве рішення Вправа 4*.2 Добудувати фронтальну проекцію відрізка АВ, якщо відомо, що

відрізок у просторі нахилений до горизонтальної площини проекції під кутом у 30°. Проекція точки А2 зображена графічно (див. б та в).

Вправа 4*.3 Побудувати горизонтальну та фронтальну проекції відрізка L(L1, L2), якщо задані графічно горизонтальний М та фронтальний N сліди цього відрізка. Побудувати просторове зображення відрізка (див. а, б).

а б в – для вправи 4*.4 Вправа 4*.4 Через точку А провести пряму, що перетинає відрізок ВС та пара-

лельна фронтальній площині проекцій (див. в).

Вправа 4*.5 Побудувати фронтальну та профільну проекції прямої загального положення АВ = 60 мм. Визначити кути нахилу прямої АВ до площини проекцій П1, П2 та П3. На епюрі відрізок заданий проекцією А1В1 та проекцією точки В2.

40