Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный авиационный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Higher_Mathematics_Part_3

.pdf

Скачиваний:

304

Добавлен:

19.02.2016

Размер:

9.11 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1617 / 2417 18 19 20 21 22 23 24 > Следующая >>>

In this case evaluation of the integral can be done in different ways. For example, we can restore the function u(x, y), using the approach

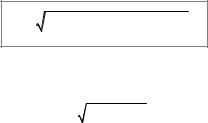
of solution of the differential equation of the first order in total differentials. The simplest way is to integrate along a broken line (Fig. 7.7) whose parts are parallel to axes of coordinates.

Thus, we receive

у	М	В
у1	М	В
у1		L
		L
у	А	К
0		К
О	х0	х1	х

Fig. 7.7

∫ P(x, y)dx + Q(x, y)dy = ∫ P(x, y)dx + Q(x, y)dy =

L AKB

= ∫ P(x, y)dx + Q(x, y)dy + ∫ P(x, y)dx + Q(x, y)dy =

	AK	KB
	x	y
	= ∫1 P(x, y0 ) dx + ∫1 Q(x1 , y)dy.
	x0	y0
Theorem	Let functions	P(x, y, z) , Q(x, y, z) and R(x, y, z) be conti-

nuous together with their partial derivatives of the first order in a simply connected domain D. Then the line integral

∫ P(x, y, z)dx + Q(x, y, z)dy + R(x, y, z)dz ,

is independent of the path of integration if and only if the next equalities hold

∂P	=	∂Q	,	∂Q	=	∂R	,	∂R	=	∂P .
∂y		∂x		∂z		∂y		∂x		∂z

In this case the integrand expression is a total differential of the function u(x, y, z) , i.e.

P(x, y, z)dx + Q(x, y, z)dy + R(x, y, z)dz = du(x, y, z)

and

∫ P(x, y, z)dx + Q(x, y, z)dy + R(x, y, z)dz =

= u(xB , yB , zB ) − u(xA , yA , zA ),

where A(xA , yA , zA ) and B(xB , yB , zB ) are initial and terminal points of the path of integration L.

161

http://vk.com/studentu_tk, http://studentu.tk/

7.7.Application of Line Integral

1.Length L of a plane or space curve is evaluated by the formula

L = ∫ dl.

In particular:

а) if a space curve is given by the equations x = x(t), y = y(t), z = z(t), t [α, β], then

L = ∫ (x′(t))2 + ( y′(t))2 + (z′(t))2 dt;

b) if a plane curve is given by the equation			y = y(x) ,		x [а; b], then

	b
	L = ∫	′	2	dx.	(7.11)
	L = ∫	1+ ( y (x))		dx.	(7.11)
	a

2. Area Р of a part of the cylindrical surface (Fig.7.2). The surface is formed by its directrix АВ lying in the plane Охy and its elements perpendicular to that plane, and bounded from above by the surface determined by the non-negative

function z = f (x, y) .P is defined by the formula:

P = ∫

f (x,

y)dl.

(7.12)

3. Mass m of a material curve L is evaluated by the formula

m = ∫ γ(x, y)dl,

where γ (x, y) is the line density of the curve L at the point M (x,

y) .

4. Coordinates xc ,

yc of the gravity center of the curve L may be found by

formulas

∫ xγ (x, y)dl

∫ yγ (x, y)dl

(7.13)

= L

, y

= L

5. Area S of the plane figure lying in the plane Оху and bounded by a closed contour L is evaluated by the formula

162

http://vk.com/studentu_tk, http://studentu.tk/

	S =	1	∫ xdy − ydx.	(7.14)
		2
			L
6. Work done by a force
F = P(x, y, z)i + Q(x, y, z) j + R(x, y, z)k
(functions P(x, y, z), Q(x, y, z),			R(x, y, z) are continuous over the space

curve L) at moving a material point along the curve L is defined by the formula

A = ∫ P(x, y, z)dx + Q(x, y, z)dy + R(x, y, z)dz.

If a curve L lies in the plane Оху, the work done by the force

F = P(x, y)i +

+Q(x, y) j at moving a material point along the curve is

A = ∫ P(x, y)dx + Q(x, y)dy.

(7.15)

Micromodule 7

EXAMPLES OF PROBLEM SOLUTIONS

Example 1. Evaluate line integrals of the first type:

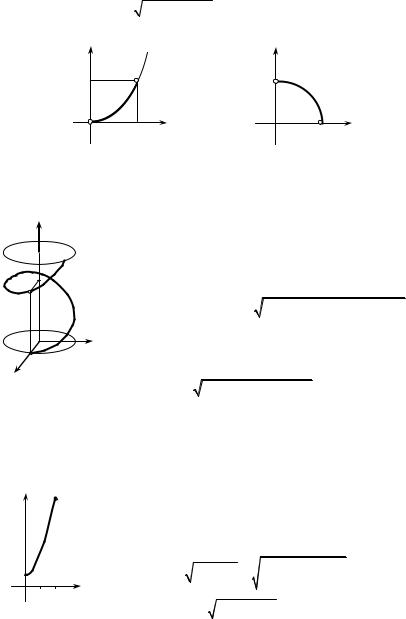
а) ∫ xdl, where AB is the arc of the parabola y = x2

from the point A (0; 0)

up to the point B (1; 1) (Fig. 7.8);

b) ∫ x2 ydl where L is an arc of the circumference

x2 + y2

= 1 lying in the

first quarter (Fig. 7.9).

Solution. а) We can find

y′ = 2x and receive by the formula (7.2)

∫ xdl = ∫ x

1+ 4x2 dx =

∫

1+ 4x2 d(1+ 4x2 ) =

(1+ 4x2 )3

(5 5 −1).

b) We can rewrite the equation of the circumference in the parametric form:

x = cos t, y = sin t, 0 ≤ t ≤	π	. Then we have by the formula (7.4)
	2

163

http://vk.com/studentu_tk, http://studentu.tk/

cos3 t

∫ x2 ydl = ∫2 cos2 t sin t

sin2 t + cos2 tdt = −∫2 cos2 td(cost) = −

Fig. 7.8

Fig. 7.9

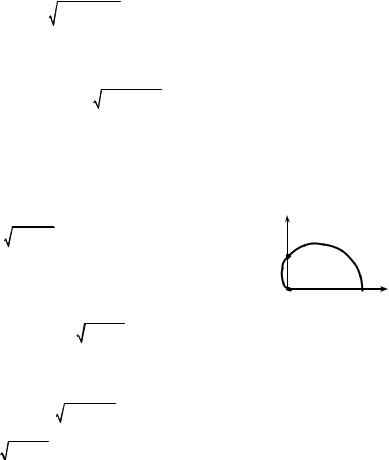
Example 2. Determine the mass of a screw line described by the equations

x = 3cos t,

y = 3sin t,

z = 4t, 0 ≤ t ≤ 2π (Fig. 7.10) if the density

at each

point

(x, y, z)

of the line is

defined

by the

formula

γ (x, y, z) = 2z.

Solution. The mass of the given space curve may be

8π

defined by the formula

m = ∫ γ(x(t), y(t), z(t)) (x′(t))2 + ( y′(t))2 + (z′(t))2 dt.

′

As γ(x, y, z) = 2z = 2 4t = 8t,

x (t) = −3sin t,

z (t) = 4 ,

3 у

y′(t)

= 3 cos t, therefore

2π

Fig. 7.10

m = ∫ 8t

9sin2 t + 9cos2 t + 16dt =

20t2

= 80π2 .

Example 3. Find coordinates of the gravity center of a homogeneous arc of

the chain line

y =	ex + e− x	, 0	≤ x ≤ ln 2 (Fig. 7.11).
	2

Solution. As the gravity center of a homogeneous arc does not depend on the value of density we shall consider it to be equal to 1. Then the mass of the arc will be numerically equal to the length of this arc. Taking into account that

					′ 2			1			x		− x		2
1	2		1+ ( y )			=	1+	4	(e			− e		)		=
О	2	х		1	(ex	+ e− x )2 =				1	(ex + e− x ),
			=

	Fig. 7.11			2					2
	Fig. 7.11			2					2

164

http://vk.com/studentu_tk, http://studentu.tk/

we receive by the formula (7.11)

ln 2

l = m =

∫ (ex

+ e− x )dx =

(ex − e− x )

After using the formula (7.13) we find

ln 2

( y′ (x))2 dx =

ln 2

(x (ex + e− x ))dx =

(ex − e− x )

ln02 −

xc =

∫ x 1+

∫

ln 2

(ex − e− x )dx =

2 x (ex

− e− x )

ln 2

− (ex

+ e− x )

ln 2

= 1 (3ln 2 − 1);

− ∫

4 ln 2

′

4 ln 2 ex + e− x

+ e− x

yc =

∫

y 1+ ( y (x))

∫

dx =

1 ln 2

−2 x

1 1

2 x

−2x

ln 2

∫ (e

2 + e

)dx =

(

+ 2x −

)

4 + 2 ln 2

−

(16ln 2 +

15).

Example 4. Evaluate the line integral of the first

type ∫

x2 + y2 dl

where

L is

the

upper

half

the

cardioid ρ = 1+ cos ϕ (Fig. 7.12).

Solution. We pass to polar coordinates

the

2 х

formulas

x = ρ cos ϕ ,

y = ρ sin ϕ , then

x2 + y2

ρ .

Fig. 7.12

So as ρ′ = − sin ϕ ,

ρ2 + (ρ′)2

= (1+ cos

ϕ)2 + sin2 ϕ = 2

+ 2 cos ϕ = 4 cos2 ϕ

′

ϕ [0; π] ,

+ (ρ )

= 2

cos

= 2cos 2

for

then ∫

∫ρ 2cos

+ y

dl =

2dϕ = ∫(1+ cos ϕ) 2cos

2dϕ =

4 cos

= ∫ 2 cos

= 8∫

1− sin

d sin

3 ϕ

= 8 sin

−

sin

= 8

1−

165

http://vk.com/studentu_tk, http://studentu.tk/

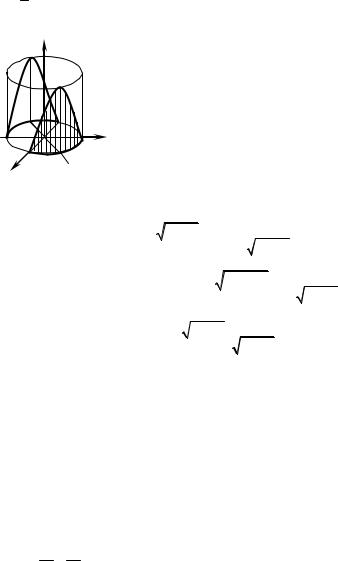
Example 5. Evaluate the area of the lateral surface of the circular cylinder x2 + y2 = 4 bounded by the plane Оху and by the hyperbolic paraboloid

z = 14 xy (Fig. 7.13).

	О	2 y
x	2	у = х

	Fig. 7.13

Solution. Proceeding from the geometrical meaning of a line integral of the first type, the problem is reduced to evaluation of the line integral of the function


f (x, y) =		1	xy	( f (x, y) ≥ 0) over the	circumference

x2 + y2	4				f (x; y) ≥ 0 for
	= 4		(the formula (7.12)). As
x ≥ 0 ,	y ≥ 0			and x ≤ 0, y ≤ 0 , and the surface z =		xy

is symmetric relative to the plane y = x					4
					it is possible to

reduce the evaluation of the integral only along the fourth part of the circumference which lies in the first quarter of the plane. We receive

y = 4 − x2 , y′ = −	x	,

4 − x2

1+ ( y′)2 =	4	, dl = 1	+ ( y′)2 dx =		2dx		,
	− x2				4 − x2
4
	2		2			2
P = ∫ f (x, y)dl = 2∫ x 4 − x2				dx = 2 x2			= 8.

L	0		4 − x2			0

Example 6. Evaluate line integrals of the second type:

а) ∫ x2 dx + xydy if АВ is a line segment connecting the points А(1; 1) and

В(2; 3) (Fig. 7.14);

b) ∫ (x − y)dx + (x + y)dy if L is the broken line ОАВ, where O(0;0), A(2;0),

В(2;3) (Fig. 7.15);

c) ∫ xdx + y2 dy if AB is the arc of the parabola y = x2 from the point A(0;

0) to the point B (2; 4) (Fig. 7.16);

d) ∫ dx − dy if L is the first quarter of the circumference x2 + y2 = 4 (direc-

L y x

tion of motion is clockwise).

166

http://vk.com/studentu_tk, http://studentu.tk/

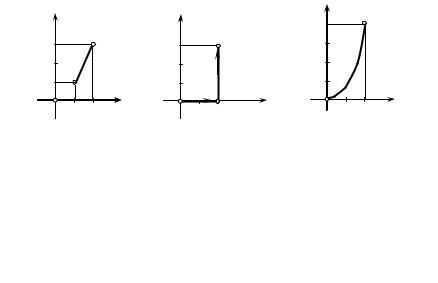
у		у			у	В
у		у			4

	В
3	В	3	В
1	А		А
О	1 2 х	О	А	х	А	2	х
О	1 2 х	О	2	х	А	2	х
Fig. 7.14			Fig. 7.15			Fig. 7.16

Solution: а) We can write down an equation of the straight line passing

through two points A (1; 1) and B (2; 3):	x − 1	=	y − 1	, i.e.	y = 2x − 1. The
	2 − 1		3 − 1

equation of the segment АВ is: y = 2x − 1, 1 ≤ x ≤ 2 . And by the formula (7.7) we receive:

	2	2	26
∫ x2 dx + xydy = ∫(x2 + x(2x − 1) 2)dx = ∫(5x2 − 2x)dx =			26	.
∫ x2 dx + xydy = ∫(x2 + x(2x − 1) 2)dx = ∫(5x2 − 2x)dx =			3	.
AB	1	1	3

b) We can rewrite the integral as a sum of two integrals, first of which we take over the line segment ОА, and the second one over the line segment АВ. For

the segment ОА y = 0, dy = 0, 0 ≤ x ≤ 2, therefore

			2
	∫ (x − y)dx + (x + y)dy = ∫ xdx = 2.
	OA		0
For the segment AB x = 2 , dx = 0 , 0 ≤ y ≤ 3 , therefore
		3		y2	3		9
		3		y2	3		9
∫ (x − y)dx + (x + y)dy = ∫(2 + y)dy = 2 y +					= 6 +			= 10,5.
∫ (x − y)dx + (x + y)dy = ∫(2 + y)dy = 2 y +					= 6 +			= 10,5.
AB		0		2	0		2
So,	∫ (x − y)dx + (x + y)dy = 2 + 10, 5 = 12, 5.
	L
c) We have (see Fig. 7.16):
			2	4		70
∫ xdx + y2 dy = ∫ xdx + ∫			y2 dy = ∫ xdx + ∫ y2dy =			70			.
∫ xdx + y2 dy = ∫ xdx + ∫			y2 dy = ∫ xdx + ∫ y2dy =						.
AB	AB	AB	0	0			3

d) We can rewrite the equation of the given circumference arc in the para-

metrical form: x = 2 cos t, y = 2sin t, 0 ≤ t ≤	π	. Then x′(t) = −2sint, y′(t) = 2cost.
Using the formula (7.6) we receive:	2
Using the formula (7.6) we receive:
		167

http://vk.com/studentu_tk, http://studentu.tk/

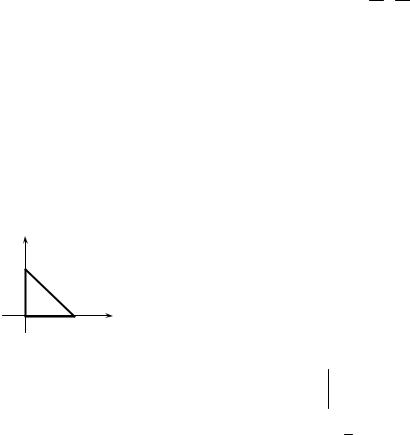
	dx		dy	0		2sin t		2 cos t		0	π
											2
∫		−		= ∫	−		−		dt = −2∫ dt = 2∫ dt = π.
	y		x			2sin t
AB				π				2 cos t		π	0
				2						2

Example 7. Evaluate the area of the domain bounded by the ellipse x2 + y2 = 1. a2 b2

Solution. We can rewrite the equation of the ellipse in parametrical form:

x = a cos t, y = b sin t,				t [0; 2π] . For			evaluation of the area			we apply the
formula (7.14). Then
	1				1	2π
S =	1	∫ xdy − ydx =			1	∫ (a cos t bsin t + bsin t a sin t )dt =
S =	2	∫ xdy − ydx =			2	∫ (a cos t bsin t + bsin t a sin t )dt =
		L		0
			ab	2π				ab	2π
		=	ab	∫ (cos2 t + sin2 t)dt =				ab	∫ dt = πab.
		=	2	∫ (cos2 t + sin2 t)dt =				2	∫ dt = πab.
				0			0
Example 8. Evaluate the line integral							I = ∫ (x2 + y2 )dx + xdy			using Green’s

formula if L is a set of sides of the triangle whose vertices are the points A (0; 0), B(1; 0), C(0; 1) (Fig. 7.17).

Solution. We have P = x2 + y2 , Q = x,

∂Q

−

∂P

= 1− 2y . By the formula (7.9) we receive

∂x

∂y

х + у = 1

∫ (x2 + y2 )dx + xdy = ∫∫(1− 2 y)dxdy

where the domain D is the triangle ОАВ. As an equation

Fig. 7.17

of the side AB looks like х + y = 1, then

1 1− x	1
I = ∫∫ (1− 2 y)dxdy = ∫ dx ∫	(1− 2 y)dy = ∫ ( y − y2 )

D		0 0
	1
	∫	(1− x − (1− x)2 )dx =
=		(1− x − (1− x)2 )dx =
	0
		(1;2)

Example 9. Evaluate I = ∫ (x2 +

			0
	(1− x)2		(1− x)3	1

−		+

	2		3	0

y)dx + (x + 2 y)dy.

(0;0)

1− x

dx =

= 16 .

Solution. We should check up the condition of the line integral to be path-

independent: P = x2 + y , Q = x + 2y ,	∂P	=	∂Q	= 1 .
	∂y		∂x
168

http://vk.com/studentu_tk, http://studentu.tk/

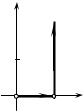
As the condition (7.10) is fulfilled, the integral is pathindependent. We can move from the point (0; 0) to the point (1; 2) along the broken line ОАВ (Fig. 7.18). We have for ОА: y = 0, dy = 0, 0 ≤ x ≤ 1; on АВ: х = 1, dx = 0, 0 ≤ y ≤ 2 .

So,

1		2		x	3	1			2		19			1

I = ∫ x	2	dx + ∫ (1	+ 2 y)dy =			+ ( y + y	2	)		=			= 6		.
				3					0			3		3
0		0				0

2 В

		А
О	1	х

Fig. 7.18

Example 10. Evaluate the work done by the force F = y2 i + x j at moving a material point along the line segment connecting the points A (1; 2) and B (2; 4).

Solution. It is necessary to evaluate the line integral of the second type of functions P = y2 and Q = x along the line segment АВ. We can write down an

equation of the segment АВ:						x − 1				=			y − 2	,	from here			y = 2x . By the formula
equation of the segment АВ:										=				,	from here			y = 2x . By the formula
(7.14) we have						2 − 1						4 − 2
(7.14) we have																	2			4
																	2			4	y
A = ∫ y2 dx + xdy = ∫										y2 dx + ∫					xdy = ∫ 4x2 dx + ∫						y	dy =
A = ∫ y2 dx + xdy = ∫										y2 dx + ∫					xdy = ∫ 4x2 dx + ∫						2	dy =
AB							AB						AB				1			2	2
AB							AB						AB				1			2
	4	x	3	2	y2			4			4					1			37
	4		3	2	y2			4			4					1			37
=				+					=				(8 −1)		+		(16 − 4)	=		.
=	3			+	4				=		3		(8 −1)		+	4	(16 − 4)	=	3	.
	3			1	4			2			3					4			3

Example 11. Evaluate the line integral

∫ (

)

(

− cos y

)

if L

x3 + 2xy dx +

is the ellipse x2 + 4 y2

= 4 .

Solution. Since ∂P

∂(x3 + 2xy)

= 2x,

∂Q =

∂(x2 − cos y)

2x,

then ∂P =

∂Q

∂x

∂y

∂x

∂y

but the line integral over any closed contour L is equal to zero.

Example 12. Evaluate the line integral

I = ∫ (x2 + 2z)dx + (x − y)dy +

+ (x + 2z)dz if L is a line segment connecting the points A(2; 0; −1) and B(4; 1; 2).

Solution. Let us write down parametrical equations of the straight line АВ:

x − 2

y − 0

z + 1

x − 2

= y =

z + 1

= t.

4 − 2 1− 0 2 + 1

Thus x = 2t + 2, y = t, z = 3t − 1 are parametrical equations of the straight line АВ.

169

http://vk.com/studentu_tk, http://studentu.tk/

Coordinates of the point A may be received from the parametrical equations for t = 0 ; and t = 1 corresponds to the point B. So, on the segment АВ t [0; 1] .

Taking into account that dx = 2dt, dy = dt, dz = 3dt, we can pass from the line integral to the definite one:

I = 1 (((2t + 2)2 + 2(3t − 1)) 2 + (2t + 2 − t) + (2t + 2 + 2(3t − 1)) 3)dt =

∫

0
1	2		8		3		53		2		1
1	2		8		3		53		2		1
= ∫ (8t		+ 53t + 6)dt =		t		+		t		+ 6t
= ∫ (8t		+ 53t + 6)dt =	3	t		+	2	t		+ 6t
0			3				2				0

= 83 + 532 + 6 = 35 16 .

Micromodule 7

CLASS AND HOME ASSIGNMENTS

Evaluate line integrals of the first type.
1.	∫ sin3 x cos xdl if L is the arc of the curve					y = ln sin x ,	x [π / 6; π / 2].
	L
2.	∫ y2 dl			if L is the cycloid arc x = t − sin t,		y = 1− cos t	( 0 ≤ t ≤ 2π).
	L
3.	∫		dl	if L is the line segment connecting the points А(–2; 0) and В(4;0).
3.	∫	x	− y
	L	x	− y
	L
4.	∫ xy−4 dl if L is the arc of the hyperbola				xy = 1 between two points А(1; 1)
	L
and В(2; 1/2).
5.	∫		x2 + y2 dl if L is the circumference		x2 + y2 = 2x .
	L
6.	∫		x2 + y2 + 1dl if L is the arc of Archimed’s spiral				ρ = ϕ bounded by
	L
two points А(0; 0) and В(1; 1).
7.	∫ xy2 dl			if L is the circumference arc x = R cos t, y = R sin t ( 0 ≤ t ≤ π / 2 ).
	L
8.	∫ (x2 + y2 + z2 )dl if L is the arc of the screw line						x = cos t, y = sin t,
	L
z = bt ( 0 ≤ t ≤ 2π ).
9.	∫ (2x − 3y + z + 4)dl if L is the line segment connecting the points А(1; 3; –1)
	L

and В(2; 0; 3).

170

http://vk.com/studentu_tk, http://studentu.tk/

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1617 / 2417 18 19 20 21 22 23 24 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
19.02.20169 Mб95Higher_Mathematics_Part_1.pdf
#
19.02.20166.63 Mб1052Higher_Mathematics_Part_1.pdf
#
19.02.20169.73 Mб45Higher_Mathematics_Part_2.pdf
#
19.02.20167.48 Mб408Higher_Mathematics_Part_2.pdf
#
19.02.20167.31 Mб123Higher_Mathematics_Part_2.pdf
#
19.02.20169.11 Mб304Higher_Mathematics_Part_3.pdf
#
19.02.2016694.82 Кб11HiraganaKatakanaWorkSheet (1).pdf
#
11.09.2019192.23 Кб1hjuj;f.docx
#
27.11.2019386.05 Кб9How Airplanes Work.doc
#
20.11.201958.78 Кб8I exercise 5.docx
#
19.02.201615.51 Mб28IFPS.pdf