Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный авиационный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Higher_Mathematics_Part_3

.pdf

Скачиваний:

304

Добавлен:

19.02.2016

Размер:

9.11 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 2410 11 12 13 14 15 16 17 18 19 20 21 22 23 24 > Следующая >>>

Definition. A function F(ω) presented by formula (4.7), is called Fourier transformation for the function f (x) . Formula (4.6) gives inverse Fourier transformation for the function F(ω) .

A function f (t) is called an original and a function F(ω) is called its

transform.

Fourier formula (4.5) can be written in symmetric form :

1) if a function

f (x)

is even then

∞

f (x) =

∫

(ω) cos ωxdω,

∞

FC (ω) =

∫

f (t) cos ωtdt;

where

f (x)

is odd then

2) if a function

2 ∞

f (x) =

∫

F (ω) sin ωxdω,

where

2 ∞

FS (ω) =

∫

f (t) sin ωtdt.

Definition. A function FC (ω)

is called Fourier cosine-transform and FS (ω)

is called Fourier sine-transform of a function f (x) .

Definition. Functions

F(ω) ,

FC (ω) ,

FS (ω) are called spectrum density of a

function f (x).

We can write a complex function F(ω) as

F(ω) = F(ω) eiϕ(ω) , − ∞ < ω < ∞ .

Definition. A modulus of spectrum density A (ω) = F(ω) is called an

amplitude spectrum and an argument of a conjugate function ϕ(ω) = arg F(ω) is called a phase spectrum of a function f (x) . They give an amplitude and a phase of a fluctuation with a frequency ω correspondently.

http://vk.com/studentu_tk, http://studentu.tk/

Fourier transformation is used for many tasks solution in mathematical physics, electronics, digital processing of signals and so on.

Micromodule 4

EXAMPLES OF PROBLEMS SOLUTION

Write a function f (x) as a Fourier integral. Find the spectrum density, amplitude and a phase spectrum of a function f (x) . Sketch the graphs of a function f (x) , an amplitude and a phase spectrum.

	e−2x , if		x ≥ 0,
Example 1.
Example 1.	f (x) =
		0, if	x < 0.
		0, if	x < 0.

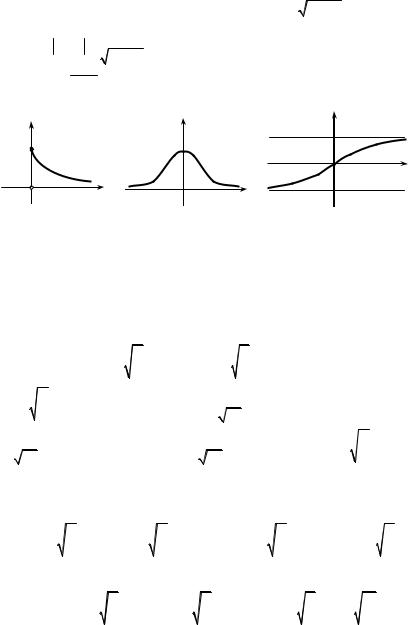
Solution. Fig. 4.1 gives the graph of the function f (x) . Let’s prove this function to be absolutely integrable:

∞	0			∞		e	−2x	A

∫		f (x)	dx = ∫ 0 dx + ∫ e−2xdx = lim

						−2
−∞			−∞	0	A→∞			0

Let’s find the spectrum density using formula (4.7)

= 12 < ∞ .

∞				∞					∞
F(ω) = ∫ f (t)e−iωt dt = ∫ e−2t e−iωt dt = ∫ e−(2+iω)t dt =
−∞			0						0
=	lim	e−(2+iω)t		A	=		1	=	2 − iω	.
=	lim				=			=	4 + ω2	.
	A→∞ −(2 + iω)			0		2	+ iω		4 + ω2

We substitute the value of spectrum density in formula (4.6) and get the expansion of the given function in Fourier integral

	1	∞	2 − iω
f (x) =		∫		eiωx dω.
	2π		2
		−∞ 4 + ω

This equality is fulfilled for all real x except x = 0 . For x = 0 the following formula is true:

1	∞	2 − iω		1
	∫		eiωx dω =		.
2π		2		2
	−∞ 4 + ω

Let’s find the amplitude and the phase spectrum:

F(ω) =

F(ω)

earg F (ω) ,

F(ω)

2 − iω

4 + ω2

http://vk.com/studentu_tk, http://studentu.tk/

		2		ω		1		ω
arg F(ω) = arctg	−ω /(4 + ω )		= − arctg		, F(ω) =		e−i arctg	2 ,
	2 /(4 + ω2 )			2		4 + ω2

A(ω) = F(ω) =	1	is the amplitude spectrum (Fig. 4.2),

4 + ω2

ϕ(ω) = arg F(ω) = arctg ω2 is the phase spectrum (Fig. 4.3)

f(x)		А(ω)			φ(ω)
f(x)		А(ω)			π/2
1			0,5
1
					О	ω
	х			ω
О	х		О	ω	–π/2
Fig. 4.1			Fig. 4.2		Fig. 4.3
Example 2.		sin x, if	\| x \|≤ π,
	f (x) =	sin x, if	\| x \|≤ π,
	f (x) =	0, if	\| x \|> 0.
		0, if	\| x \|> 0.

Solution. The given function is absolutely integrable, bounded and piecewise monotone on a finite segment (Fig. 4.4). Therefore we can expand it in Fourier

integral. The function f (x) is odd. Then we find its Fourier sine-transform:

2 ∞

F (ω) =

π ∫

f (t) sin

ωtdt =

∫

sin t sin ωtdt =

(cos(1− ω)t − cos(1+ ω)t ) dt =

sin(1− ω)t

sin(1+ ω)t

∫

−

2π

− ω

1+ ω

sin(1− ω)π

sin(1+ ω)π

sin ωπ

2 sin ωπ

−

= =

1− ω

1+ ω

− ω

1+ ω

2π

π 1− ω

where ω ≠ 1.

For ω = 1 we get

(1) =

π sin2 tdt =

π (1− cos 2t)dt

t −

sin 2t

π .

π ∫0

2 π ∫0

2 π

Furthermore,

lim

F (1) =

lim

sin ωπ

lim π cos ωπ =

−π =

π .

ω→1

ω→1 1− ω2

ω→1

−2ω

π −2

http://vk.com/studentu_tk, http://studentu.tk/

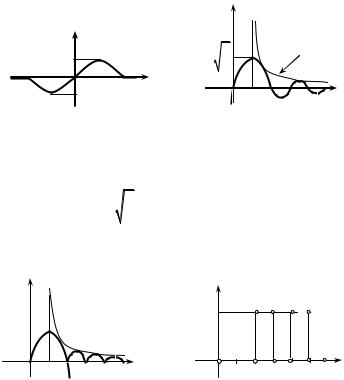
That is, Fourier sine-transform

FS (ω) is a continuous function on [0; ∞)

(Fig. 4.5).

The expansion of the given function in Fourier integral looks like

∞ sin ωπ

f (x) =

∫

sin ωxdω.

1− ω

This equality is fulfilled for all real x .

FS(ω)

f(x)

1 − ω2

–π

π х

1 2

–1

3 4

Fig. 4.4

Fig. 4.5

Let’s find the amplitude and the phase spectrum:

sin ωπ

> 0,

A(ω) =

FS (ω)

sin ωπ

1− ω

, ϕ(ω) =

sin ωπ

1− ω2

π,if

< 0.

1− ω

Let’s consider the graphs of functions

A(ω), ϕ(ω)

(Fig. 4.6 and 4.7).

А(ω)

φ(ω)

О 1

3 4

2 3 4 5 ω

Fig. 4.6

Fig. 4.7

Micromodule 4

CLASS AND HOME ASSIGNMENTS

Write a function f (x)

as Fourier integral. Find the spectrum density,

amplitude and the phase spectrum of a function f (x).

Sketch the graphs of a

function f (x), amplitude and phase spectrum.

http://vk.com/studentu_tk, http://studentu.tk/

x, if	\| x \|≤ 1,	cos πx, if \| x \|≤ 0,5,
1. f (x) =	\| x \|> 1.	2. f (x) =
0, if	\| x \|> 1.	0, if \| x \|> 0,5.

3. Find the amplitude and the phase spectrum of the function

1, if 1 ≤ x ≤ 2,

f (x) =		x < 1 або x > 2.
0, if
4. Find Fourier transformation of the function
cos(x / 2), if			\| x \|≤ π,
f (x) =	0,	if	\| x \|> 0.

5. Write the function f (x) as a Fourier integral
x, if	0 ≤ x < 1,

f (x) = 1, if 1 ≤ x < 2,
	x ≥ 2.
0, if

Answers

∞ sin2 ω

2sin2 ω

f (x) =

∫

cos ωxdω, x R, FC (ω) = A(ω) =

ϕ(ω) = 0.

2. f (x) =

cos

∞

cos 2

2π

якщо ω ≠ π,

cos 2

∫

cos ωxdω,

x R, FC (ω) =

− ω

A(ω) =

2π

π2

− ω2

π2 − ω2

якщо ω = π,

8π

cos

0, якщо

≥ 0,

π2 − ω2

3. A(ω) =

3ω

F(ω) =

4cos πω

ϕ(ω) =

sin

, ϕ(ω) =

cos

2π

1 − 4ω2

π, якщо

< 0.

− ω

∞

sin ω

cos 2ω

∫

−

sin ωxdω.

http://vk.com/studentu_tk, http://studentu.tk/

Micromodule 4

SELF-TEST ASSIGNMENTS

Write a function f (x) as Fourier integral.

0, if x ≤ 0,

1.f (x) = sin x, if 0 < x < π,0, x ≥ π.if

0, if x ≤ 0,

3.f (x) = cos, if 0 < x < π,0, if x ≥ π.

	2, if		0 < x < 3,
5.		1, if	x = 3,
	f (x) =
			x > 3.
	0, if
		0,	if x < 0,
7.		1− x, if 0 ≤ x ≤ 1,
	f (x) =
		0,	if x > 1.

	0, if		x < 0,
9.
	f (x) = x, if 0 ≤ x ≤ 1,
			x > 1.
	0, if


	1+ x, if − 1 < x < 0,
2.
	f (x) = 1− x, if 0 ≤ x < 1,
		0, if \| x \|≥ 1.

	0, if		x < −1,
4.		1, if	− 1 ≤ x ≤ 0,
	f (x) =
			x > 0.
	0, if
	4, if		0 < x < 2,
6.			x = 2,
	f (x) = 2, if
			x > 2.
	0, if
		0,	if x < 0,
8.		πx, if 0 ≤ x ≤ 1,
	f (x) =
		0,	if x > 1.

		6, if	0 < x < 4,
10. f (x) =			x = 4,
		3, if
			x > 4.
		0, if

Find the Fourier sine-transform of the function f (x) .

11. f (x)

13. f (x)

15. f (x)

	0 ≤ x ≤ 2,			x, if	0 ≤ x ≤ 1,
1, if		12.	f (x) =
=	x > 2.				x > 1.
0, if			0, if
2, if 0 ≤ x ≤ 3,		14.	2x, if 0 ≤ x ≤ 1,
=	x > 3.		f (x) =		x > 1.
0, if			0, if
2x + 1, if 0 ≤ x ≤ 1,		16.	x −1, if 0 ≤ x ≤ 2,
=	x > 1.		f (x) =		x > 2.
0, if			0, if

Find the Fourier cosine-transform of the function f (x) .

		0 ≤ x ≤ 4,			x, if	0 ≤ x ≤ 1,
17.	1, if		18.	f (x) =
	f (x) =	x > 4.				x > 1.
	0, if			0, if

http://vk.com/studentu_tk, http://studentu.tk/

19. f (x)

21.f (x)

23.f (x)

2, if	0 ≤ x ≤ 2,
=	x > 2.
0, if	x > 2.

sin x, if 0 ≤ x ≤ π,
=	x > π.
0, if	x > π.
1,	if 0 ≤ x ≤ 1,

=2 − x, if 1 < x < 2,0, if x ≥ 2.

20.	x + 1, if		0 ≤ x ≤ 1,
	f (x) =	0, if	x > 1.

=e− x , if 0 ≤ x ≤ 1,

22.f (x)

0, if x > 1.

2, if 0 ≤ x ≤ 1,

24.f (x) = 3 − x,if 1 < x < 3,0, if x ≥ 3.

Find the amplitude and the phase spectrum of the function f (x).

	0, if	x < 0,
25.	f (x) = 1, if	0 ≤ x ≤ 2,
	0, if	x > 2.
	0, if	x ≤ 1,
27.	f (x) = 1, if	1 < x ≤ 2,
	0, if	x > 2.
	0, if	x < 2,
29.	f (x) = 1, if	2 ≤ x ≤ 3,
	0, if	x > 3.

	0, if	x < 0,
26.	f (x) = 2, if	0 ≤ x ≤1,
	0, if	x >1.
	0, if	x <1,
28.	f (x) = 2, if	1 ≤ x ≤ 3,
	0, if	x > 3.
	0, if	x < 4,
30.	f (x) = 3, if	4 ≤ x ≤ 5,
	0, if	x > 5.

http://vk.com/studentu_tk, http://studentu.tk/

Моdule

MULTIPLE INTEGRALS. LINE AND SURFACE INTEGRALS.

FIELD THEORY

MODULE STRUCTURE

Micromodule 5. Double integral. Principal concepts and definitions. Conditions of the existence and properties of calculation. Change of variable in double integral. Application of double integrals.

Micromodule 6. Triple Integrals. Principal concepts and definitions. Conditions of the existence and properties. Cylindrical and Spherical coordinates. Change of variable in double integral. Application of double integrals.

Micromodule 7. Line integrals of the first and second type. Properties and evaluation. Green’s formula. Conditions for a line integral being pathindependent. Integration of total differentials. Application.

Micromodule 8. Surface integrals of the first and of the second type. Properties and evaluation. Gauss — Ostrogradsky’s formula. Stokes formula.

Micromodule 9. Field theory. Scalar and vector fields. Gradient of a scalar field. Directional derivative. Flux, circulation, divergence, rotation of the vector field. Gauss — Ostrogradsky’s formula. Stokes’ formula. Hamiltonian operator. Potential, solenoidal, harmonic fields. Differential operations of the first and second orders.

Micromodule 5

BASIC THEORETICAL INFORMATION. DOUBLE INTEGRALS

Double integral. Principal concepts and definitions. Conditions of the existence and properties of calculation. Change of variable in double integral. Application of double integrals.

Key words: double integral — подвійний інтеграл; integral sum — інтегральна сума; iterated (repeated) integral — повторний інтеграл, directrix — директриса, generatrices — твірні, nonhomogeneous material plate — неод-

норідна матеріальна пластина, mass of a planar figure — маса плоскої фігури; moment of inertia — момент інерції; static moment of inertia — статичний момент інерції.

Literature: [3, chapter 2, section 2.3], [9, chapter 10, § 1], [15, chapter 12, п. 12.1], [16, chapter 14, § 1—10], [17, chapter 2, § 7].

http://vk.com/studentu_tk, http://studentu.tk/

5.1. Problem Leading to the Concept of Double Integral

In this chapter we shall discuss the main problems connected with the integration of functions of two variables. The definitions and results obtained can be extended functions of three and more variables.

a) Problem of computing the volume of a cylindrical body

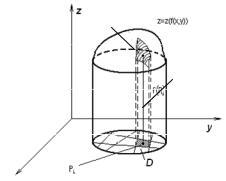
Let a body in space be bounded from above by the graph of a continuous and nonnegative function z = f (x, y), which is defined in the domain D,

from the sides by a cylindrical surface whose directrix is the boundary of the domain D and whose generatrices are parallel to the z-axis, and from below by the domain D lying in the ху-plane. A body of this shape is a curvilinear cylinder (Fig. 5.1).

	z	Δδi
	z
				z = z(f(x, y))
				z = z(f(x, y))
					f(Pi)
					f(Pi)
		Si				y





x	Pi		D
x	Pi	Fig. 5.1
		Fig. 5.1

A domain D is called the base of the cylindrical body. This is the orthogonal projection on the ху-plane of the surface that bounds the cylindrical body. We have closed bounded domain D. We denote the volume of the cylindrical body

by V. Let’s find volume V.

Now we break the base D of the cylindrical body into n nonintersecting


squarable domains Di ,		(i = 1, 2, ...n) of arbitrary shape such that they have no
common internal points. We call them partial domains or regions. Let their areas
be Si , i = 1, 2...n.
In every regions Di		we take arbitrary points	Pi (ξi ,ηi ) . Find the value of a
function at these points		f (Pi ) = f (ξi , ηi ).
We can consider the volume Vi of each Di			to be approximately equal to
f (ξi , ηi ) Si	= Vi . It is the volume of cylindrical pillar, where its generatrix is a
parallel to the	z — axis, the base is Di and the altitude h = f (Pi ). There exists
n pieces of pillars.

Then the volume of the whole cylinder is to be approximately equal to the sum

http://vk.com/studentu_tk, http://studentu.tk/

n	n
Vn = ∑Vi = ∑ f (ξi , ηi ) Si		(5.1)
i=1	i=1

It is intuitively clear that Vn ≈ V.

The diameter λ(D) of a bounded closed domain D is the largest distance between two points of a boundary of this domain. Let denote λ as the largest diameter of Di ,

λ = max λ(Di )

(5.2)

1≤i≤ n

Then the volume V is a limit, as λ → 0

V = limVn

= lim

∑ f (ξi , ηi ) Si .

(5.3)

λ →0

i=1

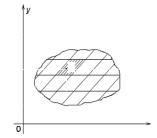
b) Problem of computing the mass of a plate

Let’s

consider,

on the

—

plane, a

nonhomogeneous material plate. A domain D

has the mass m. γ(x,

y) is the density. Proceeding

from the density γ(x, y), we calculate the mass

m of the plate assuming that

γ(x,

is a

continuous function.

divide

into

parts

arbitrarily

Di , i = 1, 2, ...n, so that they have no common

internal points. The masses of the subdomains

are mi .

Their areas are equal to

Si .

In each

Fig. 5.2

region Di we arbitrarily take a point Pi (ξi , ηi ).

Find density at the points γ(ξi , ηi ).

We may consider the mass

mi of each Di to be approximately equal to

γ(ξi , ηi ) Si = mi .

The mass m of the whole plate is approximately equal to the sum

= ∑mi =∑ γ(ξi , ηi ) Si ,

(5.4)

i=1

which is the integral sum for the continuous function γ(x, y)					in the domain D.
Passing to the limit, as λ → 0,		we shall evidently get the exact value of the mass
of the plate

				n
	m = lim mn		= lim ∑γ(ξi , ηi ) Si .		(5.5)
	λ →0		λ →0	i=1
				i=1
100

http://vk.com/studentu_tk, http://studentu.tk/

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 2410 11 12 13 14 15 16 17 18 19 20 21 22 23 24 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
19.02.20169 Mб95Higher_Mathematics_Part_1.pdf
#
19.02.20166.63 Mб1052Higher_Mathematics_Part_1.pdf
#
19.02.20169.73 Mб45Higher_Mathematics_Part_2.pdf
#
19.02.20167.48 Mб408Higher_Mathematics_Part_2.pdf
#
19.02.20167.31 Mб123Higher_Mathematics_Part_2.pdf
#
19.02.20169.11 Mб304Higher_Mathematics_Part_3.pdf
#
19.02.2016694.82 Кб11HiraganaKatakanaWorkSheet (1).pdf
#
11.09.2019192.23 Кб1hjuj;f.docx
#
27.11.2019386.05 Кб9How Airplanes Work.doc
#
20.11.201958.78 Кб8I exercise 5.docx
#
19.02.201615.51 Mб28IFPS.pdf

x, if	\| x \|≤ 1,	cos πx, if \| x \|≤ 0,5,
1. f (x) =	\| x \|> 1.	2. f (x) =
0, if	\| x \|> 1.	0, if \| x \|> 0,5.