Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный авиационный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Higher_Mathematics_Part_3

.pdf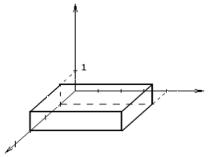

Скачиваний:

304

Добавлен:

19.02.2016

Размер:

9.11 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 1415 / 2415 16 17 18 19 20 21 22 23 24 > Следующая >>>

Solution. The domain of integration is a rectangular parallelepiped (Fig. 6.5). Then the triple integral can be reduced to the formula (6.14). We have

						z
						1				4	y
						1

			x 3				Fig. 6.5
							Fig. 6.5
							3	4	1
		∫∫∫(x + y + 2z)dxdydz = ∫ dx∫ dy∫(x + y + 2z)dz =
		G					1	0	0
3	4		2		1	3	4			3				y2	4
3	4		2		1	3	4			3				y2	4
= ∫ dx∫((x + y)z + z				)		dy = ∫ dx∫(x + y + 1)dy = ∫					(x + 1) y +				dx =
= ∫ dx∫((x + y)z + z				)		dy = ∫ dx∫(x + y + 1)dy = ∫					(x + 1) y +			2	dx =
1	0				0	1	0			1				2	0
	3							3
		= ∫(4x + 12)dx = (2x2 + 12x)						= 18 + 36 − 2 − 12 = 40.
	1							1
Example 2. Calculate the triple integral									∫∫∫	xdxdydz			over the domain
Example 2. Calculate the triple integral									∫∫∫	(1+ 2y + z)		3	over the domain
		x = 0, y = 0 , z = 0 , x + y + z =							D	(1+ 2y + z)
D = {(x, y)									1}.
D = {(x, y)									1}.

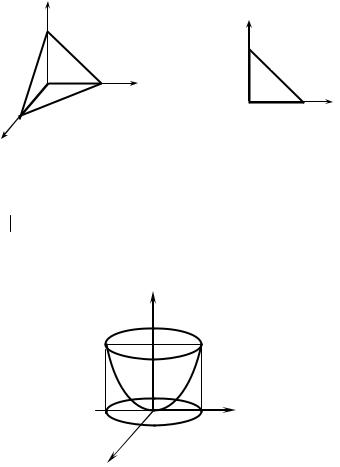
Solution. The domain of integration is a rectangular triangular pyramid bounded by coordinate planes and sloping plane x + y + z = 1 (Fig. 6.6).

Let’s define limits of integration in a triple integral. Projecting the given body on the xy-plane, we shall receive domain D. It is a triangle ОАВ (Fig. 6.7.),

which boundaries are determined by the equations

x = 0,

y = 0,

x + y = 1 (on

the xy-plane

z = 0 ).

We have

xdxdydz

1− x

1− x− y

∫∫∫

= ∫ xdx ∫

∫

(1+ 2y + z)

(1+ 2 y + z)

1− x

1− x− y

1− x

dy =

∫

xdx

dy = −

∫

xdx

∫

−

∫

− x + y)

+ 2y)

−2(1+ 2y + z)

141

http://vk.com/studentu_tk, http://studentu.tk/

	1	1						1						1				1− x							1	1					1					1				1
= −		∫ x		−							+									dx = −						∫ x									−				−		dx =
= −	2	∫ x		−		2 − x + y					+	2(1+								dx = −					2	∫ x		2(2x − 3)							−		x − 2		−	2	dx =
	2	0				2 − x + y						2(1+			2y)			0							2	0		2(2x − 3)									x − 2			2
			1	1	1						3							2				x					1				3			3
	= −			∫				1	+					− 1−						−			dx			= −			−			x	+			ln		2x − 3			−
	= −			∫				1	+					− 1−						−			dx			= −			−			x	+			ln		2x − 3			−
			2	0			4			2x − 3							x	− 2			2						2				4			8
										−2ln			x −		2	−	x2		1		=		1	− ln 2 +				3		ln 3.
																	x2		1				1					3

																	4						2					16
																			0
																			0
							z
							1 C																						у
																												1			В		x + y = 1
																																	x + y = 1

ОB

1 у

1 х

Fig. 6.6 Fig. 6.7

Example 3. Calculate the triple integral ∫∫∫(x2 + y2 ) dxdydz over the domain

G = {(x, y) z = 3, x2 + y2 = 3z }.

Solution. The domain of an integration G (Fig. 6.8.) is bounded by the paraboloid x2 + y2 = 3z and the plane z = 3.

– 3

Fig. 6.8

142

http://vk.com/studentu_tk, http://studentu.tk/

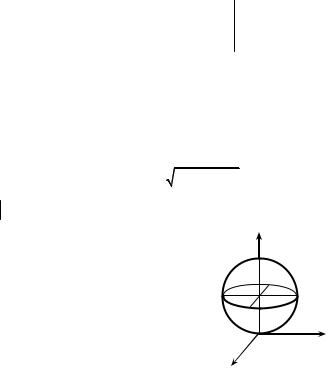
A projection of this domain on xy-plane is a circle x2 + y2 = 9 (this equation is a result of an elimination of a variable z from the system of the equations

x2 + y2 = 3z and z = 3 ).
Let’s consider cylindrical coordinates x = ρ cosϕ,			y = ρsin ϕ, z = z. The
equation of a paraboloid can be written as the form	z =	ρ2		, and the equation of
			3

a plane is not changed. Let’s define limits of integration in cylindrical coordinates

0 ≤ ϕ ≤ 2π, 0 ≤ ρ ≤ 3,	ρ2	≤ z ≤ 3.
	3

Then we have

2π	3	3	2π	3
				3

∫∫∫(x2 + y2 )dxdydz = ∫ dϕ∫ dρ ∫ ρ2 ρdz = ∫ dϕ∫ρ3 z																									ρ2		dρ =
	G									0		0			ρ2						0	0			3
																3									3
																3
2π	3	3		ρ2							2π	3				3	ρ5				2π	3ρ4			ρ6			3
2π	3	3		ρ2							2π	3				3	ρ5				2π	3ρ4			ρ6			3
= ∫ dϕ∫ρ		3 −				d			ρ = ∫ dϕ∫					3ρ −				dρ = ∫						−				dϕ =
= ∫ dϕ∫ρ		3 −		3		d			ρ = ∫ dϕ∫					3ρ −			3	dρ = ∫				4		−	18			dϕ =
0	0			3						0		0					3				0	4			18			0
		2π	35				35				3		243			2π			243				243π
		2π	35				35				3		243			2π			243				243π
	= ∫				−						dϕ =					∫ dϕ =					2π =					.
	= ∫		4		−			6			dϕ =			12		∫ dϕ =			12		2π =			6		.
		0	4					6			0			12		0			12					6
Example 4. Calculate the triple integral																		∫∫∫		x2 + y2 + z2 dxdydz over the
																		G

domain G = {(x, y) x2 + y2 + z2 = 2z}.

Solution. Lets consider the equation x2 + y2 + z2 = 2z.

It is a sphere. Let’s transform it to the canonical form. After determination of the perfect square, we obtain

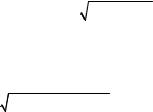
x2 + y2 + (z − 1)2 = 1. Therefore centre of the sphere lies in

a point (0; 0; 1) and radius is equals 1 (Fig. 6.9).

The form of the domain G, and also kind of intergrand

function specify the necessity of realization of calculation	O	y
of a triple integral in spherical coordinates.	x
In spherical coordinates the equation x2 + y2 + z2 = 2z	Fig. 6.9
can be written as ρ2 = 2ρ cos θ or ρ = 2cos θ. We have:	Fig. 6.9
can be written as ρ2 = 2ρ cos θ or ρ = 2cos θ. We have:
0 ≤ ϕ ≤ 2π, 0 ≤ θ ≤ π , 0 ≤ ρ ≤ 2cos θ.
2
		143

http://vk.com/studentu_tk, http://studentu.tk/

Besides,			x2 + y2 + z2 = ρ,
				J = r2 sin θ.
Applying the formula (6.25), we obtain
				2π			π	2cos θ
				2π			2	2cos θ
∫∫∫ x2 + y2 + z2 dxdydz = ∫ dϕ∫ dθ ∫										ρ ρ2 sin θdρ =
Ω				0			0	0
2π	π		2cos θ		2π		π
2π	2		2cos θ	3	2π		2			ρ4	2cos θ		dθ =
= ∫ dϕ∫sin θdθ ∫				ρ dρ = ∫			dϕ∫sin θ			4	0		dθ =
= ∫ dϕ∫sin θdθ ∫				ρ dρ = ∫			dϕ∫sin θ				0
0	0		0		0		0
2π	π						2π	π
2π	2						2π	2
= ∫	dϕ∫ 4cos4θ sin θdθ = −4						∫ dϕ∫cos4 θd(cos θ) =
0	0						0	0
		4	2π	π	4	2π			4			8π
			2π	2 dϕ =		2π
	= −		∫ cos5 θ				∫ dϕ =			2π =			.


	5		0	0	5		0	5				5
	5		0	0	5		0	5				5

Example 5. Find the volume of the body bounded by the surfaces		y = x,
x + y − 4 = 0, + z − 2 = 0, = 0, z = 0.
Solution. Let’s construct the	body (Fig. 6.10). The plane y = x	passes
through z-axis and intersects plane	Оху along a straight line y = x .

The plane x + y − 4 = 0 is parallel to the axis Oz and intersects a plane Оху along a straight line x + y − 4 = 0 . The plane x + z − 2 = 0 is parallel to the axis

Oу and intersects with the plane Oхz along a straight line x + z − 2 = 0 . The projection of the given body on the ху-plane is the triangle OMK. Using the formula (6.27) we have

	2		4− x		2− x		2	4− x			2− x					2	4− x
V = ∫∫∫ dxdydz = ∫ dx ∫				dy ∫ dz = ∫ dx ∫ z							2− x		dy = ∫(2 − x)dx ∫ dy =
G	0		x		0		0		x		0					0	x
2		4− x		2										2		(4 − 4x + x2 )dx =
2				2										2
= ∫(2 − x) y			= dx∫		(2 − x)(4 − 2x)dx = 2∫
0		x		0										0
			= 2		4x − 2x	2	+	x3		2	=	16			.
						2		x3		2		16

								3					3
								3		0			3

Example 6. Find the volume of the body bounded by the surfaces x2 + y2 = 4, z = y2 , z = 0.

144

http://vk.com/studentu_tk, http://studentu.tk/

Solution. Let’s construct our body (Fig. 6.11). The surface x2 + y2 = 4 is the infinite circular cylinder which intersects xy-plane along the circle x2 + y2 = 4 with the centre in origin and with the radius R = 2. The surface z = y2 is the

infinite parabolic cylinder which intersects yz-plane along the parabola z = y2 . The plane z = 0 is xy-plane.

	z
	2		z
	2
x + z = 2			z = y2
x + z = 2			K	G
	O		K	G
	2	4	y
4	М	D	D	2	y
4	x + y = 4		D	2	y
	x + y = 4

	x	x = y
	x	x
		x
	Fig. 6.10	Fig. 6.11

The obtained body projects on xy-plane in a circle D. Therefore we shall conduct calculations in the cylindrical coordinates (6.20)

				x = ρ cos ϕ, y = ρ sin ϕ,									z = z.
The equation of parabolic cylinder transforms to															z = ρ2 sin2 ϕ, and the
equation of circle	x2 + y2 = 4 transforms to the form ρ = 2. Let’s define limits
of an integration:
Hence		0 ≤ ϕ ≤ 2π,			0 ≤ ρ ≤ 2,				0 ≤ z ≤ ρ2 sin2 ϕ.
Hence
					ρ2 sin2 ϕ							2π	2		2			2	ϕ ρdρ =
					ρ2 sin2 ϕ							2π	2		2			2
V = ∫∫∫ dxdydz = ∫∫ρdρdϕ						∫		dz = ∫ dϕ∫ z							ρ	sin
G				D		0				0			0		0
2π		2		2 3	2π	2	ϕ	ρ4			2			2π			2	ϕdϕ =
2π		2		2 3	2π	2		ρ4			2			2π			2
= ∫ sin			ϕdϕ∫ρ dρ = ∫ sin						4			dϕ = 4 ∫ sin
0				0	0				4		0		0
	= 22π			1− cos 2ϕ dϕ =		2		ϕ −				sin 2ϕ		2π	= 4π.
												sin 2ϕ		2π

			∫	(	)					2
			0							2				0
Example 7. Find the volume of a body bounded by the spheres x2 + y2 + z2 = a2 ,
x2 + y2 + z2 = b2	(a < b) and a cone x2 + y2								= z2 .
																			145

http://vk.com/studentu_tk, http://studentu.tk/

Solution. Let’s construct such body (Fig. 6.12). Clearly that for a solution of a problem it is necessary to enter spherical coordinates (6.23)

x = ρ sin θ cos ϕ, y = ρ sin θ sin ϕ, z = ρ cos θ .

θ = π4 a	b
a	y

Fig. 6.12

Let’s find limits of integration. As the equation of our spheres x2 + y2 + z2 = a2 ,

x2 + y2 + z2

= b2 in the spherical coordinates is

ρ = a

and

ρ = b

correspon-

dently, then

a ≤ ρ ≤ b.

The projection of the body on the xy-plane is the whole

circle, then

0 ≤ ϕ ≤ 2π. Now we find the limits for angle θ.

We substitute the

spherical coordinates into the equation of the given cone. Then

ρ2 sin2 θ cos2 ϕ + ρ2 sin2 θ sin2 ϕ = ρ2 cos2 θ,

ρ2 sin2 θ = ρ2 cos2 θ

tan2 θ = 1.

Hence θ = π . It is clear that, 0 ≤ θ ≤

π .

Using the formula (6.29) we find the volume of the given body

2π

V = ∫∫∫ρ2 sin θdρdθdϕ = ∫ dϕ∫ dθ∫ρ2 sin θdρ =

Ω*

2π

− a

2π

= ∫

dϕ∫sin θ

∫ (− cos θ)

dθ =

04 dϕ =

2π

− a3

2π

− a3

−

+ 1 dϕ =

−

+ 1

= (b

− a

)(1

− 2)

∫

146

http://vk.com/studentu_tk, http://studentu.tk/

Example 8. Find the coordinates of the center of mass of a uniform hemisphere of radius R.

Solution. Suppose that the centre of the sphere lies at the origin of coordinates, and that the hemisphere lies below the xy-plane. Then by symmetry we have

xc = 0, yc = 0.

The volume of the hemisphere is

V = 23 πR3.

Now we find the static moment relative to the xy-plane

2π

Kxy = ∫∫∫ zdxdydz = ∫

dϕ∫sin θ cos θdθ∫ρ3dρ =

= 2π

sin2 θ

π ρ4

0 4

Therefore

Kxy

zc =

πR4 / 4

2πR3

/ 3

Micromodule 6

CLASS AND HOME ASSIGMENTS

Establish limits of an integration in a triple integral ∫∫∫ f (x, y, z)dV over a

domain G, if							G
domain G, if
1.	x = 0 , y = 0 , z = 0 , 3x + 6y + 4z − 24 = 0 .
2.	x = 0 , y = 0 , x = 2 , y = 3 , z = 0 , z = 3 + y.
3.	x2 + y2 = 4 , z = −1 , z = 4.
Calculate the integral.
	1	1	2		1	1− x	1− x− y	dz
4. ∫ dx∫ dy∫				(x + 2y + 4z)dz .	5. ∫ dx ∫		dy ∫	dz		.
4. ∫ dx∫ dy∫				(x + 2y + 4z)dz .	5. ∫ dx ∫		dy ∫	(3x + 2y + z − 4)	4	.
	0	0	0		0	0	0	(3x + 2y + z − 4)
	1	2− y		1
6.	∫ dy ∫		dx∫(x2 + y)zdz.
	0	y2		0

Calculate the triple integral in Rectangular coordinate system.

7. ∫∫∫ x2 yzdxdydz , if the domain G is bounded by planes x = 0 , y = 0 ,

z = 0 and x + y + z = 2 .

147

http://vk.com/studentu_tk, http://studentu.tk/

8. ∫∫∫ (x + y + z)dxdydz, if the domain G is bounded by planes x = 0 , y = 0 ,

z = 0 , x = 1, y = 1, z = 1.

9. ∫∫∫ x2 dxdydz , if the domain G is bounded by the surfaces x2 + y2 = 1 and

z = 0, z = 3.

Evaluate the followіng integrals using cylindrical coordinates.

10.	∫∫∫ (x2 + y2 + z2 )dxdydz, if the domain G is bounded by the surfaces
	G
x2 + y2	= 4 and z = 0 , z = 1.
11.	∫∫∫ zdxdydz , if the domain G is bounded by the surfaces z2 = x2 + y2
	G
and z = 2 .
12.	∫∫∫ (x + y2 + z2 )3 dxdydz , if the domain G is bounded by the surfaces
	G
x = y2 + z2		and x = 1.
Evaluate the followіng integrals using spherical coordinates.
13.	∫∫∫	x2 + y2 + z2 dxdydz , if the domain	G is bounded by the sphere
	G
x2 + y2 + z2 = y.
14.	∫∫∫ (x2 + y2 )dxdydz , if the domain G ={(x, y), z ≥ 0 ,			x2 + y2 + z2 ≤ 1.}.
	G
15.	∫∫∫ (x2 + y2 + z2 )2 dxdydz , if G is sphere		x2 + y2 + z2	≤ R2 .
	G

Calculate the volume of the followіng body.

16.	z = 4 − x2 ,	z = x2 + 2,		y = −1,	y = 2.
17.	z = x2 + y2 ,	z = 1.
18.	z = 2 − x2 − y2 ,		z =	x2 + y2	(cone).
19.	x2 + y2 + z2	= 4,	x2 + y2 + z2 = 9, z2 = x2 + y2 , z ≥ 0.

Calculate the mass of the followіng body with the density γ(x, y, z) .

20.z = x2 + y2 , z = 4, γ(x, y, z) = (x2 + y2 + z)2 .

21.x2 + y2 + z2 = R2 , γ(x, y, z) = (x2 + y2 + z2 )3 .

148

http://vk.com/studentu_tk, http://studentu.tk/

Answers

			4−	x			24−3x−6 y										2 3 3+ y															2		4− x2
		8	4−	2				4									2 3 3+ y															2		4− x2
	1. ∫dx ∫					dy		∫			f (x, y, z)dz.						2. ∫dx∫dy ∫ f (x, y, z)dz.												3. ∫ dx ∫ dy ×
		0	0					0									0			0		0									−2		−		4− x2
																	0			0		0									−2		−		4− x2
4											1			27			16					3		3			28π									π
× ∫											1			27			16					3		3			28π									π
	f (x, y, z)dz.						4. 11. 5.							. 6.			. 7.			.	8.		. 9.		π. 10.					.	11.		4π . 12.			2 .
	f (x, y, z)dz.						4. 11. 5.						144	. 6.	42		. 7.	315		.	8.	2	. 9.	4	π. 10.			3		.	11.		4π . 12.			2 .
−1									4πR7																										4πR9
	π		4						4πR7							π			5π			19(2 −			2)π				448π						4πR9
13.		. 14.			π. 15.							. 16. 8. 17.					. 18.			.	19.					. 20.						. 21.				.
13.	10	. 14.	15		π. 15.					7		. 16. 8. 17.				2	. 18.		6	.	19.	3				. 20.		3				. 21.		9		.
	10		15							7						2			6			3						3						9
														Micromodule 6
										CLASS AND HOME ASSIGMENTS
	6.1. Calculate the triple integral																∫∫∫ f (x, y, z)dxdydz. The function f(x, у, z)
																	V
and surfaces bounding the volume V are given in Table 6.1.																																		Table 6.1
																																		Table 6.1

	№					f(x, у, z)																	Domain V

	1					5y – 4								x = 0, y = 0, z = 0, x + y + 2z – 6 = 0.

	2					6y + 2z								x = 0, y = 0, z = 0, 3x + y + z – 9 = 0.

	3				5 + y +2х									x = 0, y = 0, z = 0, 2x + 3y + z – 2 = 0.

	4					4x–y								x = 0, y = 0, z = 0, 4x + y + 2z – 1 = 0.

	5					3 + 4z								x = 0, y = 0, z = 0, x + 4y + z – 4 = 0.

	6					7y – 2z								x = 0, y = 0, z = 0, 3x + y + 3z – 6 = 0.

	7					xy + 1								x = 0, y = 0, z = 0, 6x + 2y +z – 8 = 0.

	8					3y –2 z								x = 0, y = 0, z = 0, 7x + y + z – 3 = 0.

	9					2x + z								x = 0, y = 0, z = 0, 4x + 2y + 4z – 1 = 0.

	10					3 + 4z								x = 0, y = 0, z = 0, 8x + 2y + 2z – 3 = 0.

	11					4y + 5								x = 0, y = 0, z = 0, 3x + y + z – 6 = 0.

	12					3x + 2								x = 0, y = 0, z = 0, 7x + y + 7z – 14 = 0.

	13					3xy								x = 0, y = 0, z = 0, 2x + 4y + z – 8 = 0.

	14					8y – 2z								x = 0, y = 0, z = 0,5x + y + 10z – 10 = 0.

	15					5x + z								x = 0, y = 0, z = 0, 3x + 2y + 6z – 6 = 0.

	16					7 – 4z								x = 0, y = 0, z = 0, 4x + y + 2z – 8 = 0.

	17					3x + 2y								x = 0, y = 0, z = 0, 6x + 3y + z – 18 = 0.
																																				149

http://vk.com/studentu_tk, http://studentu.tk/

		End of table 6.1

№	f(x, у, z)	Domain V

18	3xy + 2	x = 0, y = 0, z = 0,x + 15y + z – 15 = 0.

19	6z + 3	x = 0, y = 0, z = 0, 2x + y + 5z – 10 = 0.

20	4x + y	x = 0, y = 0, z = 0, 3x + 4y + z – 12 = 0.

21	xy	x = 0, y = 0, z = 0, 4x + 2y + 3z – 12 = 0.

22	5 – 8z	x = 0, y = 0, z = 0,x + 3y + 15z – 15 = 0.

23	y +2	x = 0, y = 0, z = 0, x + 5y + 3z – 15 = 0.

24	y – 6z	x = 0, y = 0, z = 0, 2x + 5y + z – 10 = 0.

25	2x – y	x = 0, y = 0, z = 0, 3x + 6y + 2z – 12 = 0.

26	3 – 2z	x = 0, y = 0, z = 0, x + 2y + 4z – 8 = 0.

27	х + 3y	x = 0, y = 0, z = 0, 8x + y + 2z – 8 = 0.

28	2z + 1	x = 0, y = 0, z = 0, 4x + 6y + 3z – 12 = 0.

29	2x + y	x = 0, y = 0, z = 0, 2x + 9y + 2z – 18 = 0.

30	у + 4z	x = 0, y = 0, z = 0, x + 5y + 4z – 20 = 0.

6.2. Calculate the volume of a body bounded by the following surfaces. Use the cylindrical and spherical coordinates.

6.2.1.x2 + y2 + z2 = 1 , x2 + y2 + z2 = 9 , z =

6.2.2.x2 + y2 + z2 = 4 , x2 + y2 + z2 = 9 , z =

6.2.3.	x2 + y2 + z2	= 4 ,	z =	x2 + y2 .
6.2.4.	x2 + y2 + z2	= 16 ,	y =	x2 + z2 .
6.2.5.	x2 + y2 + z2	= 4 ,	z =	3(x2 + y2 ) .
6.2.6.	x2 + y2 + z2	= 4 ,	3z =	x2 + y2 .

6.2.7.z = x2 + y2 , z = 8 − x2 − y2 .

6.2.8.x = y2 + z2 , x = 18 − y2 − z2 .

6.2.9.z = 2(x2 + y2 ) , z = 12 − x2 − y2 .

6.2.10.2z = x2 + y2 , z = 6 − x2 − y2 .

6.2.11.z = x2 + y2 , z = 16 − 3(x2 + y2 ) .

6.2.12.y = x2 + z2 , y = 3 − 2(x2 + z2 ) .

6.2.13. z = 3 x2 + y2 , z = 5 − 2(x2 + y2 ) .

x2 + y2 .

x2 + y2 , (x ≥ 0, y ≥ 0) .

150

http://vk.com/studentu_tk, http://studentu.tk/

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 1415 / 2415 16 17 18 19 20 21 22 23 24 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
19.02.20169 Mб95Higher_Mathematics_Part_1.pdf
#
19.02.20166.63 Mб1052Higher_Mathematics_Part_1.pdf
#
19.02.20169.73 Mб45Higher_Mathematics_Part_2.pdf
#
19.02.20167.48 Mб408Higher_Mathematics_Part_2.pdf
#
19.02.20167.31 Mб123Higher_Mathematics_Part_2.pdf
#
19.02.20169.11 Mб304Higher_Mathematics_Part_3.pdf
#
19.02.2016694.82 Кб11HiraganaKatakanaWorkSheet (1).pdf
#
11.09.2019192.23 Кб1hjuj;f.docx
#
27.11.2019386.05 Кб9How Airplanes Work.doc
#
20.11.201958.78 Кб8I exercise 5.docx
#
19.02.201615.51 Mб28IFPS.pdf