Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный авиационный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Higher_Mathematics_Part_3

.pdf

Скачиваний:

304

Добавлен:

19.02.2016

Размер:

9.11 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 1314 / 2414 15 16 17 18 19 20 21 22 23 24 > Следующая >>>

In each of Ωi we select an arbitrary point Pi (ξi , ηi , ζi ) .Throughout Ωi , i = 1, 2, 3… n the density is almost constant and equal to μ(Pi ), i = 1, 2, ..., n .

The mass	mi of this part of the body will then be given in the approximate
relation	mi ≈ μ(Pi ) Vi .
	mi ≈ μ(Pi ) Vi .
The mass of the entire body will be
		n
	m ≈ ∑μ(Pi ) Vi .				(6.1)
		i=1
Let λ be the largest diameter of Ωi ,
i.e.	λ = max d (Ωi ),		i = 1, 2, ..., n.
	1≤i≤ n
If (6.1) has a finite limit as λ → 0,			which is independent on the way of
dividing	Ω into partial regions	and of		selection of Pi Ωi ,	this limit is
considered to be the mass of the body
		n
	m = lim	∑μ(Pi )		Vi .	(6.2)
	λ →0	i=1
		i=1

On the other hand, this limit is known as the triple integral of the function μ(P) over the domain Ω and is denoted by

∫∫∫μ(P)dV = lim		n
∫∫∫μ(P)dV = lim		∑μ(Pi )	Vi .	(6.3)
Ω	λ →0	i=1
Hence
m = ∫∫∫μ(P)dV = ∫∫∫μ(x, y, z) dxdydz.				(6.4)
Ω	Ω
Here dx dy dz is an element of volume dV			in Cartesian coordinates.

Now we will give the formal definition of the triple integral. Consider a

closed cubable domain Ω in which a bounded function			f (P(x, y, z)) , P Ω, is
defined.			I = 1, 2, 3 … n. Let their
We divide Ω into nonoverlaping cubable parts Ωi ,			I = 1, 2, 3 … n. Let their
volumes be Vi , respectively. In each of		Ωi we arbitrarily choose a point
Pi (ξi , ηi , ζi ) . Constructed sum

	n
	σ = ∑ f (ξi , ηi , ζi )	Vi	(6.5)
	i=1
is called integral sum for function f(x, y, z).
			131

http://vk.com/studentu_tk, http://studentu.tk/

Definition. If as λ → 0, the integral sum (6.5) has a limit, that is, neither dependent on the way in which Ω is broken down into Ωi nor on the choice of points Pi Ωi , then this limit is called the triple integral of the function f(x,

y, z) over Ω and is denoted by ∫∫∫ f (x, y, z)dV					or ∫∫∫ f (P)dV .
				Ω		Ω

The function		f (x, y, z)	is called integrable in			Ω. Thus by definition we
have

				n
	∫∫∫ f (x, y, z)dV = lim∑ f (ξi , ηi , ζi )					Vi		(6.6)
		Ω		λ →0 i=1
If the mass		is distributed		over the body	Ω	with volumetric		density
γ = γ(x, y, z) for any point			(x,	y, z) Ω then mass		m = ∫∫∫γ(x, y, z)dxdydz . It
is mechanical sense.							Ω
is mechanical sense.

Triple integrals are generalization of the double integrals in three — dimension region.

Theorem	(Sufficient condition). If the function f (x, y, z) is continuous in
	a closed cubable domain Ω then it is integrable in that domain.

6.2. Properties of Triple Integrals

Triple integrals are similar in their behavior to double integrals. Therefore, we can easily list their properties.

Let the functions f (P) and g(P) be integrable in a domain Ω. 1. Linearity.

∫∫∫(αf (P) + βg(P))dV = α∫∫∫ f (P)dV + β∫∫∫ g(P)dV ,

Ω Ω Ω

where α and β are arbitrary real constants.

2. If the functions f (P) ≤ g(P)	everywhere in Ω, then
∫∫∫ f (P)dV ≤ ∫∫∫ g(P)dV.
Ω	Ω

(6.7)

(6.8)

3. If f (P) ≡ 1 in Ω, then

∫∫∫ dV = V ,	(6.9)
Ω

where V is the volume of Ω.

132

http://vk.com/studentu_tk, http://studentu.tk/

Pm Ω,

4. If the function f(P) is continuous in a closed cubable domain Ω and M and m are its largest and smallest values in Ω, then

mV ≤ ∫∫∫ f (P)dV ≤ MV ,

(6.10)

where V is the volume of Ω.

5. Additivity.

If a region Ω is divide into cubable domains Ω1 and Ω2 without common

internal points and f (P)	is integrable in Ω,	then f (P)	is integrable in each of
Ω1 and Ω2 , and
∫∫∫ f (P)dV =∫∫∫ f (P)dV +∫∫∫ f (P)dV			(6.11)
Ω	Ω1	Ω2

6. Theorem (mean value). If the function f (P) domain Ω then there exists a point such as

∫∫∫ f (P)dv = f (Pm )V ,

is continuous in a closed

(6.12)

where V is the volume of Ω.
Definition. The value f (Pm ) =	1	∫∫∫Ω	f (P)dV is known as the mean value
	V
of f (P) in Ω .

6.3. Triple Integral in Cartesian Coordinates

As in the case of double integrals, the calculation of triple integrals reduces to the calculation of integrals of a lower multiplicity.

Suppose that f (x, y, z) is a continuous function in a domain Ω . Then there

exists all the integrals described below.

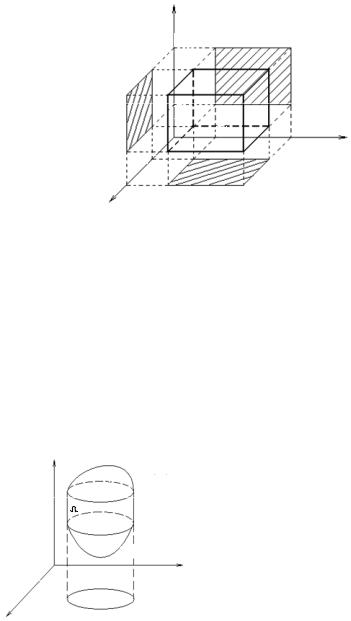
Let’s consider the case, where Ω is a rectangular parallelepiped

Ω = {a ≤ x ≤ b, c ≤ y ≤ d, l ≤ z ≤ m},

whose projection on the yz-plane is a rectangle R (Fig. 6.1). Then we will have

∫∫∫ f (x,	b
∫∫∫ f (x,	y, z)dV =∫ dx∫∫ f (x, y, z)ds.		(6.13)
Ω	a	R
			133

http://vk.com/studentu_tk, http://studentu.tk/

1
c	d

Fig. 6.1

Substituting the iterated integral for the double integral we obtain

	b	d	m
∫∫∫ f (x, y, z)dV =∫ dx∫ dy∫ f (x, y, z)dz				.	(6.14)
Ω	a	ñ	l

When Ω is a rectangular parallelepiped, we could thus reduce the taking of the triple integral to taking three conventional integrals in a series. Formula (6.13) can be rewritten

	m
∫∫∫ f (x, y, z)dv =∫∫[∫ f (x, y, z)dz]dxd y,		(6.15)
Ω	D l

where D = {a ≤ x ≤ b, c ≤ y ≤ d} is a rectangle in the xy-plane. This rectangle is

an orthogonal projection of the parallelepiped on the xy-plane.								Ω so that a
	z			Let’s consider a domain				Ω so that a
	z	S2	z = z2(x, y)	surface	S,	that bounds	Ω,	is intersected
				surface	S,	that bounds	Ω,	is intersected
				not more than at two points by any straight
				not more than at two points by any straight
				line parallel to the z-axis (Fig. 6.2).
				Let the surface S1 that bounds Ω from
		S1		below be described by the equation z = z1(x, y),
		S1	z = z1(x, y)	and the surface S2 that bounds					Ω from
			y	above	be	described	by	the	equation
		D		z = z2 (x, y). We project S1				and S2 on the
x	L	D		xy-plane into a domain D bounded by a
	L			curve L.
				curve L.
				The body Ω is bounded by a cylindrical
		Fig. 6.2		surface with a generatrix parallel to the z-
134

http://vk.com/studentu_tk, http://studentu.tk/

axis and with the curve L, which here acts as a directrix. Then by analogy with (6.15) we will obtain

	z2	( x, y)
∫∫∫ f (x, y, z)dV =∫∫[		∫ f (x, y, z)dz]dxd y.	(6.16)
Ω	D z1	( x, y)

If the domain D in the xy-plane is a curvilinear trapezoid bounded by the

curves y = ϕ1 (x) and y = ϕ2 (x),		a ≤ x ≤ b, then the double integral (6.16) can
be written in the form

		b	ϕ2 ( x)	z2 (x, y)
	∫∫∫ f (x, y, z)dv =∫ dx ∫ dy			∫ f (x, y, z)dz	(6.17)
	Ω	a	ϕ1 ( x)	z1 ( x, y)

6.3. Triple Integral in Cylindrical and

Spherical Coordinates

For more simple calculation of a triple integral, as well as for double, method of a replacement of variable frequently is used. Let’s consider the general formula.

6.3.1. Curvilinear Coordinates

Let the function f (x, y, z) be continuous in closed cubable domain functions

x = x(u, v, w),y = y(u, v, w),z = z(u, v, w)

Ω . The

(6.18)

are continuous together with their partial derivatives of the first order in a closed domain Ω*. Suppose further that the functions (6.18) establishe a one-to-one correspondence between all points (u, v, w) of Ω* and all points (x, y, z) of Ω.

A change of variables in a triple integral is performed by the following formula

∫∫∫ f (x, y, z)dxdydz =
Ω			(6.19)
= ∫∫∫ f (x(u, v, w), y(u, v, w), z(u, v, w))	I	dudvdw,


Ω*
			135

http://vk.com/studentu_tk, http://studentu.tk/

where I is the Jacobian of the set of functions (6.18):

	∂x	∂x	∂x
	∂x	∂x	∂x
	∂u	∂v	∂w
J =	∂y	∂y	∂y	≠ 0.	(6.20)
J =	∂u	∂v	∂w	≠ 0.	(6.20)
	∂u	∂v	∂w
	∂z	∂z	∂z
	∂u	∂v	∂w

6.3.2. Triple Integral in Cylindrical Coordinates

In cylindrical coordinates the position of a point M in space is determined by

three numbers ρ, ϕ, z,	where ρ,		ϕ are the polar coordinates of the projection
M onto the xy-plane and	z is termed the cylindrical coordinates of M (Fig. 6.3).
		z
		z	z
			z
				M(ρ, ϕ, z)
				y
		ϕ	ρ	y
		ϕ	ρ
	x
x

Fig. 6.3

It is clear

0 ≤ ρ < ∞, 0 ≤ ϕ < 2π, − ∞ < z < +∞.

The relation of rectangular coordinates and cylindrical coordinates is apparent from the Fig. 6.3.

x = ρ cos ϕ, y = ρ sin ϕ, z = z.

Let’s find the Jacobian

	∂x	∂x	∂x

	∂ρ	∂ϕ	∂z		cos ϕ	−ρ sin ϕ	0

J =	∂y	∂y	∂y
				=	sin ϕ	ρ cos ϕ	0	= ρ.
	∂ρ	∂ϕ	∂z
					0	0	1
	∂z	∂z	∂z

	∂ρ	∂ϕ	∂z

136

http://vk.com/studentu_tk, http://studentu.tk/

Since ρ ≥ 0, then

I		= ρ	(6.21)

and for triple integrals the formula (6.19) for the transition from rectangular coordinates to cylindrical ones becomes

∫∫∫ f (x, y, z)dxdydz = ∫∫∫ f (ρ cos ϕ, ρ sin ϕ, z)ρdρdϕdz.		(6.22)
G	G′

In cylindrical coordinates a volume element is dV = ρdρdϕdz.

Remark. Coordinates frequently pass to cylindrical, when the domain of integration derivates by a cylindrical surface, which projection on an appropriate plane is domain as a circle, annulus, sector and etc. Integrand function set as

f (x, y, z) = g(x2 + y2 , z).

6.3.3. Triple Integral in Spherical Coordinates

In spherical coordinates the position of a point M in space is determined by three numbers ρ, ϕ, θ, where ρ is the distance from the origin to the point M

(Fig. 6.4), ϕ is the angle between x-axis and the projection of the radius vector

OM of the point M on the xy-plane, θ is the angle between z-axis and the radius vector OM of M reckoned from z-axis.

M(ρ, ϕ, θ)

θρ

ϕ	y

Fig. 6.4

It is clear

0 ≤ ρ < +∞, 0 ≤ ϕ < 2π, 0 ≤ θ ≤ π.

The relation of rectangular coordinates and spherical coordinates is apparent from the Fig. 6.4.

137

http://vk.com/studentu_tk, http://studentu.tk/

x = ρ sin θ cos ϕ, y = ρ sin θ sin ϕ, z = ρ cos θ.

(6.23)

Let’s find the Jacobian

∂x

∂ρ

∂ϕ

∂θ

sin θ cos ϕ −ρ sin θ sin ϕ

ρ cos θ cos ϕ

J =

∂y

= −ρ2 sin θ.

sin θ sin ϕ

ρ sin θ cos ϕ

ρ cos θ sin ϕ

∂ρ

∂ϕ

∂θ

cos θ

−ρ sin θ

∂z

∂ρ

∂ϕ

∂θ

Therefore,

and becomes

= ρ2 sin θ

(6.24)

∫∫∫ f (x, y, z)dxdydz =

= ∫∫∫

(6.25)

f (ρ sin θ cos ϕ, ρ sin θ sin ϕ, r cos θ)ρ2 sin θdρd θd ϕ

Ω*

In spherical coordinates a volume element is dV = ρ2 sin θdρdθdϕ .

Remark. The equation of a sphere x2 + y2 + z2 = R2 in spherical coordinates can be simplified to a form ρ = R .

The spherical coordinates are frequently used, when the domain of an integration is a full-sphere, or its part or a sector. The intergrand function has a

form f (x, y, z) = g(x2 + y2 + z2 ) .
For example, if the domain is a full-sphere x2 + y2 + z2 = R2 ,				then we have
	2π	π	R
∫∫∫ f (x2 + y2 + z2 )dxdydz = ∫ dϕ∫sin θdθ∫ f (ρ2 )ρ2dρ.				(6.26)
Ω	0	0	0

6.4. Application of Triple Integrals

We shall briefly discuss typical problems of application of triple integrals and give the necessary formulas without deriving them since their derivation is similar to that of the corresponding formulas for double integrals.

1. The volume of a body.

V = ∫∫∫ dxdydz.	(6.27)
Ω

138

http://vk.com/studentu_tk, http://studentu.tk/

The volume of a body in the cylindrical coordinate can be written as

V = ∫∫∫ρdρdϕdz,

Ω1

and spherical coordinate as

V = ∫∫∫ρ2 sin θdρdθdϕ.

Ω2

2. The mass of a body.

Let in xOy some figure be given. γ(x, y, z) is density.

m = ∫∫∫ γ(x, y, z)dxdydz,

where the function γ(x, y, z) is continuous in Ω.

3. Static moments of a body relative to coordinate planes. The elementary static moment relative to the xy-plane will be dKxy = zdm = zγ(x, y, z)dV = zγ(x, y, z)dxdydz, where γ(x, y, z) is the density. The static moment is thus given by

(6.28)

(6.29)

(6.30)

Kxy = ∫∫∫ zγ(x, y, z)dxdydz.

(6.31)

Likewise, we write the static moment relative to the xz- and yz-planes

Kxz = ∫∫∫ yγ(x, y, z)dxdydz,

Kyz = ∫∫∫ xγ(x, y, z)dxdydz.

4. The coordinates of the center of mass of the body.

xc	=	∫∫∫ xγ(x,	y, z)dxdydz
		Ω		,
		∫∫∫ yγ(x,	m	,
			m
yc	=		y, z)dxdydz
		Ω			,
		∫∫∫ zγ(x,	m		,
			m
zc	=		y, z)dxdydz
		Ω		.
			m	.
			m

(6.32)

(6.33)

139

http://vk.com/studentu_tk, http://studentu.tk/

If the body is homogeneous then the density γ(x, y, z) = const We finally have

xc =	∫∫∫ xdxdydz
	Ω	,
	V	,
	V
yc =	∫∫∫ ydxdydz
	Ω		,
	V		,
	V
zc =	∫∫∫ zdxdydz
	Ω	,
	V	,
	V
where V is the volume of Ω .

5. Moment of inertia with respect to x-, y- and z- axes.

Ix = ∫∫∫( y2 + z2 )γdV ,

I y = ∫∫∫(x2 + z2 )γdV ,

in the domain.

(6.34)

(6.35)

Iz = ∫∫∫(x2 + y2 )γdV .

6. Moment of inertia with respect to xy - , yz- and xz-planes.

Ixy = ∫∫∫ z2 γdV ,

Ixz = ∫∫∫ y2 γdV ,

I yz = ∫∫∫ x2 γdV .

7. Moment of inertia with respect to the origin

I0 = ∫∫∫(x2 + y2 + z2 )γ(x, y, z) dxdydz .

(6.36)

(6.37)

Micromodule 6

EXAMPLES OF PROBLEM SOLUTIONS

Example 1. Calculate the triple integral ∫∫∫(x + y + 2z) dxdydz over the domain

G = {(x, y) x = 1, x = 3 , y = 0 , y = 4 , z = 0 , z = 1}.

140

http://vk.com/studentu_tk, http://studentu.tk/

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 1314 / 2414 15 16 17 18 19 20 21 22 23 24 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
19.02.20169 Mб95Higher_Mathematics_Part_1.pdf
#
19.02.20166.63 Mб1052Higher_Mathematics_Part_1.pdf
#
19.02.20169.73 Mб45Higher_Mathematics_Part_2.pdf
#
19.02.20167.48 Mб408Higher_Mathematics_Part_2.pdf
#
19.02.20167.31 Mб123Higher_Mathematics_Part_2.pdf
#
19.02.20169.11 Mб304Higher_Mathematics_Part_3.pdf
#
19.02.2016694.82 Кб11HiraganaKatakanaWorkSheet (1).pdf
#
11.09.2019192.23 Кб1hjuj;f.docx
#
27.11.2019386.05 Кб9How Airplanes Work.doc
#
20.11.201958.78 Кб8I exercise 5.docx
#
19.02.201615.51 Mб28IFPS.pdf