Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный авиационный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Higher_Mathematics_Part_3

.pdf

Скачиваний:

304

Добавлен:

19.02.2016

Размер:

9.11 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 1920 / 2420 21 22 23 24 > Следующая >>>

Example 2. Evaluate the surface integral of the first type I = ∫∫ z(x + 2y)dσ,

where σ is the part of the surface z = 1− x2 bounded by the planes y = 0 and y = 3 (Fig. 8.9).

	Solution. The projection of the given surface to the plane Оху is the
rectangular:			−1 ≤ x ≤ 1,		0 ≤ y ≤ 3 (Fig.	8.10). We’ll find			partial derivatives
z′	=	− x	, z′	= 0,
z′	=		, z′	= 0,
x		1− x2	y
		1− x2
	Then
		d	σ =	1+ (z′ )2 + (z′ )2 dxdy =		1+	x2	dxdy =	dxdy	.
		d	σ =	1+ (z′ )2 + (z′ )2 dxdy =		1+		dxdy =		.
				x	y	1− x2			1− x2
						1− x2			1− x2
	Now we’ll evaluate the surface integral

I = ∫∫ z(x + 2y)dσ = I = ∫∫

1− x2 (x + 2y)

dxdy

= ∫∫ (x + 2y)dxdy =

1− x2

= ∫ dx∫ (x + 2y)dy = ∫ (xy + y

)

dx = ∫ (3x + 9)dx

+ 9x

= 18.

−1

–1 O

1 х

Fig. 8.8

Fig. 8.9

Fig. 8.10

Example 3. Find

coordinates

of the centre of mass

for the

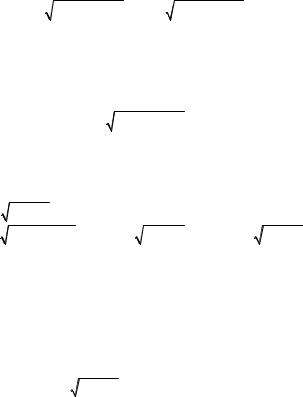
hemisphere

z = R2 − x2 − y2

(Fig. 8.11) if its surface density at each point is numerically

equal to the distance of this point to the radius, perpendicular to the basis of the hemisphere.

Solution. Under the condition of the problem the surface density at a point

(x, y, z) is defined by the formula γ = x2 + y2 . From symmetry of the hemisphere to the axis Оz and the function γ(x, y) comparatively to the point (0; 0) it follows, that the centre of mass is placed on the axis Оz. So, xc = yc = 0 and we’ll define coordinate zc accordingly the formula (8.7).

191

http://vk.com/studentu_tk, http://studentu.tk/

Let’s transform an element dσ. As

z′

− x

, z′

− y

R2 − x2 − y2

then

+ (z′ )2

= 1+

R2 − x2 − y2

and

Rdxdy

dσ =

R2 − x2 − y2

Considering that the projection of the surface to the plane Оху is the disk of

radius R, bounded with the circle x2 + y2

= R2 ,

we make calculations in polar

coordinates system. We have

x2 + y2 dxdy

2π

ρ2dρ

m = R ∫∫

= R ∫ dϕ∫

ρdρ = 2πR∫

− x

− y

− ρ

Dxy

ρ = R sin t,

= 2πR∫2

R2 sin2 t R costdt

= 2πR3 ∫2 sin2 tdt =

dρ = R costdt,

0 ≤ t ≤ π / 2

R cost

sin 2t

π2 R3

= πR

∫(1− cos 2t)dt = πR

t −

;

2π

2πR

∫∫ zγ dσ =R ∫∫

x2 + y2 dxdy =R ∫ dϕ∫ρ2dρ =

Dxy

So,

2πR4

zc =

π2 R3

3π

Example 4. Evaluate the surface integral of the second type

I = ∫∫ xdydz +

+ zdxdz + 3dxdy,

where

is the

upper

side

the

part

the plane

2x − 3y + 3z − 6 = 0 ( x ≥ 0, y ≤ 0, z ≥ 0 ).

Solution. The given surface σ, being the part of plane, is represented on the Fig. 8.12. The normal n corresponding to the upper side of the surface forms the

192

http://vk.com/studentu_tk, http://studentu.tk/

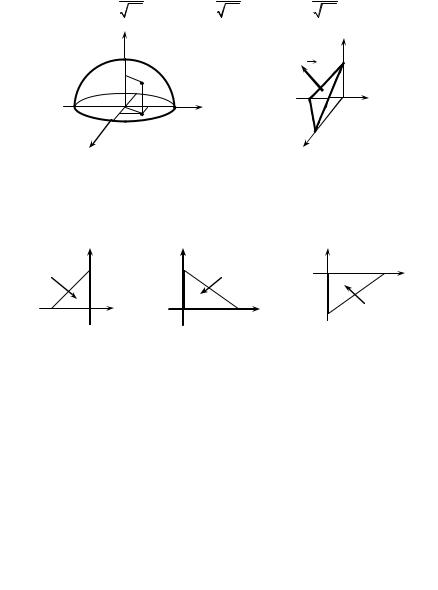
acute angles with axes Oh and Oz and the obtuse angle with the axis Оу. Actually, the normal n = {2; − 3; 3} has such directing cosines:

cos α = 2	> 0,	cosβ =	−3	< 0, cos γ =	3 > 0 .
22			22		22
z					z
R					z
R					2
					2
d					n
d
О	y	R у		–2	О у
х	y	R у
R				3
х					х
Fig. 8.11					Fig. 8.12

Therefore the surface integral is reduced to the sum of three double integrals over the domains represented on Fig. 8.13, the first and third taken with the sign «+» and the second taken with the sign «–».

	z	z		у
Dyz	2	2	Dxz	О	3 х

–2	О у	О	3 х	–2	Dxy

Fig. 8.13

So, we have

I = ∫∫ xdydz + zdxdz + 3dxdy = ∫∫ xdydz − ∫∫ zdxdz + ∫∫ 3dxdy =

Dyz

Dxz

Dxy

y+ 2

6− 2x

6 +

3y − 3z

= ∫ dy ∫

dz −∫ dx

∫ zdz +3

3 2 =

−2

(6 − 2x)2

= ∫

3y + 3 +

dy −

∫

dx + 9 = −4 − 2 + 9 = 3.

−2

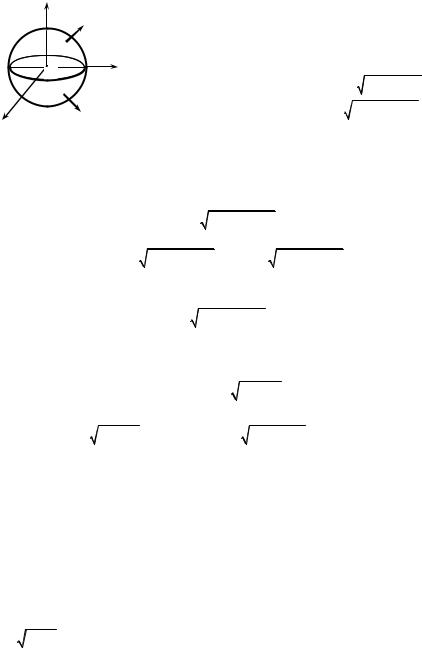
Example 5. Evaluate the surface integral of the second type ∫∫ zdxdy, if σ is

the external side of sphere x2 + y2 + z2 = R2 (Fig. 8.14).

193

http://vk.com/studentu_tk, http://studentu.tk/

z G

R n

О R у

R n

Fig. 8.14

Solution. The upper and the lower hemispheres are projected on the plane Оху in same domain, i.e.

the circle limited by a circle x2 + y2 = R2 . That is why we divide the surface σ into the part σ1 and the part

σ2 , where σ1 is the upper hemisphere z = R2 − x2 − y2 ,

and σ2	is the lower hemisphere z = − R2 − x2 − y2 .
So,	∫∫ zdxdy = ∫∫ zdxdy + ∫∫ zdxdy .
	σ	σ1	σ2

We’ll reduce each of integrals to the double one, considering, that a normal vector on the selected side of the upper hemisphere forms with the axis Oz an acute angle, and an obtuse angle with bottom hemisphere. So,

	∫∫ zdxdy = + ∫∫		R2 − x2 − y2 dxdy ,
	σ1	Dxy
∫∫ zdxdy = − ∫∫ −		R2 − x2 − y2 dxdy = ∫∫ R2 − x2 − y2 dxdy .
σ2	Dxy		Dxy
Then
	∫∫ zdxdy = 2 ∫∫		R2 − x2 − y2 dxdy = I.
	σ	Dxy

Now we’ll pass to polar coordinates and we’ll get

					2π		R
I = ∫∫ zdxdy = 2 ∫ dϕ∫								R2 − ρ2 ρdρ =
σ					0		0
R	d (R	2	− ρ	2	)		4		R		4

= 4π∫ R2 − ρ2						= −		π (R2 − ρ2 )3		=		πR3.
		−2					3				3
0									0

Example 6. Evaluate the surface integral of the second type. ∫∫ 2xdydz − ydxdz,

where σ is the external side of the part of the surface of the cylinder x2 + y2 = 1,

0 ≤ z ≤ 1, x ≥ 0, y ≥ 0 (Fig. 8.15).
Solution. We’ll consider the given integral	as the sum of two	integrals
I = I1 + I2 . For evaluation of the surface integral	I1 = ∫∫ 2xdydz we project the
	σ	0 ≤ z ≤ 1
surface σ on the plane Oyz. We’ll get the rectangular σ yz : 0 ≤ y ≤ 1,		0 ≤ z ≤ 1

(Fig. 8.16). Now we’ll solve the equation of the cylinder comparatively to the x: x = 1− y2 (the condition x ≥ 0 ). As the normal vector n at any point of the

194

http://vk.com/studentu_tk, http://studentu.tk/

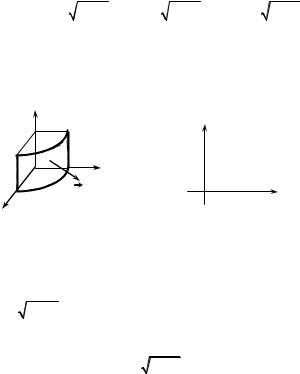
selected side of the surface σ forms with the axis Ox an acute angle, then we take the corresponding double integral with the sign «+». We have

I1 = ∫∫ 2xdydz = ∫∫ 2		1	1	1
I1 = ∫∫ 2xdydz = ∫∫ 2		1− y2 dydz = 2∫	1− y2 dy∫ dz = 2∫ 1− y2 dy =
σ	σ yz	0	0	0

y = sin t,

sin 2t

dy = cos tdt,

= ∫cos

tdt =

∫(1+ cos 2t)dt =

0 ≤ t ≤ π

/ 2

σyz

1 у

Fig. 8.15

Fig. 8.16

Similarly we evaluate the integral I2 = −∫∫ ydxdz. For this purpose we

project the surface on the plane Оxz and solve the equation of a surface with

respect to y: y = 1− x2 . Then we pass to the double integral (a sign of double integral is the same, as the sign of the surface integral). Then

		1	1	π ,
I2 = −∫∫ ydxdz = −∫ 1− x2 dx∫ dz = −				π ,
σ		0	0	4
σ		0	0
And finally we receive I = π −	π =	π .
2	4	4
Example 7. Evaluate the surface integral of the second type
I = ∫∫ x2dxdz + xdxdz + xzdxdy,
σ
where σ is the upper side of that surface part			y = x2 + z2	which is placed in the
first octant between planes y = 0 and		y = 1.

Solution. We’ll represent the surface σ. The equation y = x2 + z2 determines a paraboloid of the rotation around the axis Oy. And its part which is placed in the first octant, crosses coordinate plane Oyz on the parabola y = z2 , and plane Oxy

195

http://vk.com/studentu_tk, http://studentu.tk/

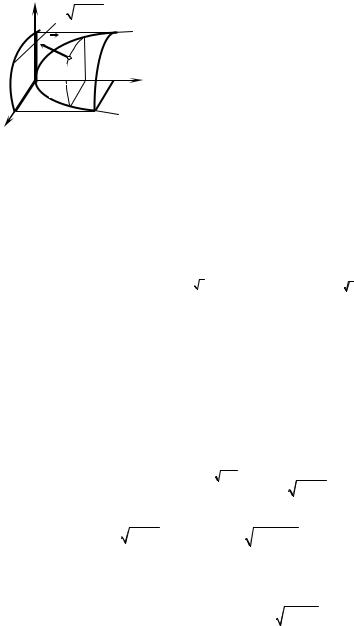
1 x

z								2
z	z = 1−x2						on the parabola	y = x . With the plane	y = 1 the
	z = 1−x2						on the parabola	y = x . With the plane	y = 1 the
1				y = z2			paraboloid is crossed along the circle x2 + z2 = 1 ,
1			σ	y = z2			paraboloid is crossed along the circle x2 + z2 = 1 ,
		n	σ				the quarter of this circle lays in the first octant.
σxz	σyz						Eventually, if	y = 0, then x2 + z2 = 0.	Only one
σxz	σyz					y	point (the Origine) satisfies this equation. As a result
		σxy			1	y	of the analysis carried we constract the surface σ
							(Fig. 8.17).		n at any
				y = x2			Let’s notice, that the normal vector		n at any
							point of the selected side of a surface		σ creates
		Fig. 8.17					acute angle with axes Ox and Oz, and it creates
							obtuse angle with the axis Oy.
Let’s evaluate three integrals in series.
1)	I1 = ∫∫ x2 dydz .
			σ

From the surface equation y = x2 + z2 it followes that x2 = y − z2 and we pass to double integral behind a projection σ yz . As the normal vector n creates acute angle with the axis Ox (see Fig. 6.16) before double integral we put a plus sign:

	2			1		y				2					1			z3	y
	2			1						2					1			z3	y
I1 = ∫∫ ( y − z		)dydz		= ∫ dy ∫ ( y − z							)dz			= ∫ yz −					dy =
I1 = ∫∫ ( y − z		)dydz		= ∫ dy ∫ ( y − z							)dz			= ∫ yz −				3	dy =
σ yz				0	0										0			3	0
σ yz				1	3						5		1						0
			2	1	3		2	2			5		1			4
		=		∫ y		dy =			y					=			.
					2							2
			3		2		3	5				2			15
			3	0			3	5					0		15

2) I2 = ∫∫ xdxdz.

The integrand does not contain variable y, therefore we pass directly to the double integral behind a projection σxz . From Fig. 8.17 it is сlear, that a normal

n corresponding to the upper side of a surface σ , creates an obtuse angle with the axis Oy, therefore double integral we take with a minus sign:

				1	1− x2		1
I2	= − ∫∫ xdxdz = −∫ xdx				∫	dz = −∫ x 1− x2 dx =
			σ xz	0	0		0
		1	1		1	2		1		1

=			∫ 1− x2 d (1− x2 ) =				(1− x2 )3		= −		.
	2				2	3				3
			0					0

3)I3 = ∫∫ xzdxdy .

σxy

From the surface equation we find that z = ± y − x2 , but we take a plus sign before the root because z ≥ 0 in the first octant, and we pass to the double

196

http://vk.com/studentu_tk, http://studentu.tk/

integral behind a projection σxy , having taken integral with a plus sign (the normal n creates an acute angle with the axis Oz):

											1			y							1	1			y
I3 = ∫∫ x		y − x2 dxdy = ∫ dy ∫ x														y − x2 dx = −					1	∫ dy ∫					y − x2 d( y − x2 ) =
I3 = ∫∫ x		y − x2 dxdy = ∫ dy ∫ x														y − x2 dx = −						∫ dy ∫					y − x2 d( y − x2 ) =
σ	xy										0		0							2		0		0
	xy
			1			1	2								y				1	1			1		2		5	1			2
						1									y					1							5	1
	= −				∫				( y − x2 )3							dy =				∫ y3 dy =						y			=			.
																											2
							3																				2			15
		2				0	3							0		3				0		3		5				0		15

So, I = I		+ I				+ I			=	4	−	1	+		2	=	1	.
So, I = I		+ I		2		+ I		3	=		−		+			=		.
	1			2				3	15		3		15			15
									15		3		15			15

Example 8. Evaluate the surface integral of the second type
										I = ∫∫ xdydz + zdxdz + 3dxdy,
												σ
where σ is the external side of the pyramid bounded by the																											x = 0,				y = 0, z = 0
and 2x − 3y + 3z − 6 = 0 (Fig. 8.12).

Solution. As the surface is closed, we apply Ostrogradsky-Gauss formula. We’ll have

P = x, Q = z, R = 3;	∂P	= 1,	∂Q		= 0,	∂R	= 0 .
Then	∂x		∂y			∂z
Then				1
I = ∫∫∫(1+ 0 + 0)dxdydz =Vpymid			=	1	3 2 2 = 4.
I = ∫∫∫(1+ 0 + 0)dxdydz =Vpymid			=		3 2 2 = 4.
G			3

Example 9. Evaluate the surface integral of the second type

I = ∫∫(x + 3z)dydz − 2ydxdz + (z − y)dxdy,

where σ is the external side of the cone part x2 + y2 = z2 placed between planes z = 0 and z = 1 (Fig. 8.18).

Solution. It is impossible to apply OstrogradskyGaussian formula to the given integral directly. On the other hand, evaluation of integral by means of designing a surface on coordinate planes leads to rather bulky calculations. We’ll apply the following method. Let’s close the surface with the circle σ1 (a part of the plane

z = 1 placed inside a cone). Then

I = I1 − I2 ,

1 σ2

σ1


Dxy	1	у
х1	1	у
х1
Fig. 8.18

197

http://vk.com/studentu_tk, http://studentu.tk/

where

I1 = ∫∫ (x + 3z)dydz − 2 ydxdz + (z − y)dxdy,

σ+σ1

I2 = ∫∫(x + 3z)dydz − 2ydxdz + (z − y)dxdy.

σ1
As
P = x + 3z, Q = −2 y, R = z − y;	∂P	+	∂Q	+	∂R	= 1− 2 + 1 = 0,
	∂x		∂y		∂z

then I1 = 0 and consequently I = −I2 , i.e. the required integral is reduced to the surface l integral over the disk σ1 . The projections of this disk on the coordinate planes Oxz and Oyz are segments. So,

I = −I2 = − ∫∫ (z − y)dxdy = − ∫∫ (1− y)dxdy.

σ1 Dxy

The sign of the double integral is not changed, as the angle between the normal vector n and the axis Oz is equal to zero ( cos γ = 1 > 0 ).

Having passed to polar coordinates in double integral, we get

I = − ∫ dϕ∫(1− ρ cos ϕ)ρdρ = − ∫

− ρ

cos ϕ

dϕ =

2π

ϕ dϕ = −

sin ϕ

2π

= − ∫

−

cos

ϕ −

= −π.

Micromodule 8

CLASS AND HOME ASSINMENTS

Evaluate the surface integral of the first type over the given surface.

∫∫(x2 + y2 + z2 )dσ,

if σ is the hemisphere

z =

R2 − x2 − y2 .

∫∫(x2 + 3y2 + z2 + 5)dσ,

if σ is the part of a cone placed between planes

y = 0

and y = 2.

∫∫ (x2 + ( y2 + z2 )2 )dσ,

if σ is the part of the plane

x + y + z = 2 , which

y2 + z2

= 1.

has been cut out by the cylinder

198

http://vk.com/studentu_tk, http://studentu.tk/

4.	∫∫(2x + 3y + 5z)dσ, if σ is the part of the plane 2x + 3y + 5z = 30, placed
	σ
in the first octant.
Evaluate the surface integral of the second type over the given surface.
5.	∫∫ ( y2 + z2 )dxdy, if σ is the external side of the cylinder part z =									9 − x2 ,
	σ	and y		= 2.
placed between planes y = 0		and y		= 2.
6.	∫∫ (x2 + y2 + z2 )dxdy,	if	σ is the external side					of a	hemisphere		part
	σ
y =	1− x2 − z2 , cut out by a cone			y =	x2 + z2 .
7.	∫∫ x2 dydz + y2dxdz + z2dxdy,			if	σ is the external			side	of a sphere		part,
	σ
placed in first octant.
8.	∫∫ zdxdy − ydydz, if σ is		triangle formed by section of a plane								6x −
	σ
− 3y + 2z = 6 with coordinate planes and a normal to the selected side creates an
acute angle with the axis Oz.
9.	∫∫ xdydz + ydxdz + zdxdy,		if σ is the external side of a sphere x2 + y2 +
	σ
+ z2 = R2 .
10. Calculate coordinates			of	mass centre		of a	homogeneous			surface
2z = 4 − x2 − y2 (z ≥ 0) .
			Answers
1.	2πR4. 2. 52 2π. 3. 29	3π / 6.		4.	450 14.	5. 88.	6.	π / 2. 7. 3πR4 /8. 8. 3.
9. 4πR3. 10. (0; 0; 307 − 15 5)/310.

Micromodule 8

SELF—TEST ASSINMENTS

8.1. Evaluate the surface integrals of the first type over the surface G (Table 8.1).

									Table 8.1

№			Integral					The equation	Additional conditions
№			Integral					of surface G	Additional conditions
								of surface G
8.1.1	∫∫(x	2	+ y	2	+ z	2	)dσ	z = x2 + y2	Surface G is bounded by
8.1.1	∫∫(x		+ y		+ z		)dσ	z = x2 + y2	planes z = 0 , z = 2
	G
									199

http://vk.com/studentu_tk, http://studentu.tk/

Continuity of table 8.1

№

Integral

The equation

Additional conditions

of surface G

8.1.2

∫∫ ydq

z =

9 − x2 − y2

8.1.3

∫∫ xyzdq

x + y + z = 1

Surface G is placed in the first

octant

8.1.4

∫∫(3z + 6x + 4y)dq

= 1

Surface G is placed in the first

octant

8.1.5

∫∫

16 − x2 − y2 dq

z = − 16 − x2 − y2

8.1.6

∫∫(x2 + y2 )dq

x2 + y2 + z2 = 4

z ≥ 0

8.1.7

∫∫ x2 z2dq

y =

25 − x2 − z2

8.1.8

∫∫

+ z

− x2 = 0

Surface G is bounded by planes

x = 0 , x = 1

8.1.9

∫∫

x2 + z2 = 16

Surface G is bounded by planes

x2 + y2

+ z2

y = 0, y = 2

8.1.10

∫∫(x2 + z2 )dq

y = 1− x2 − z2

y ≥ 0

8.1.11

∫∫

+ y

+ z

)dq

y =

x2 + z2

Surface G is bounded by planes

y = 0, y = 4

8.1.12

∫∫ xdq

z =

16 − x2 − y2

8.1.13

∫∫ y2 zdq

x + 2y + z = 1

Surface G is placed in the first

octant

8.1.14

∫∫(z + 2x + 3y)dq

= 1

Surface G is placed in the first

octant

8.1.15

∫∫

25 − x2 − z2 dq

y = −

25 − x2 − z2

8.1.16

∫∫( y2 + z2 )dq

x2 + y2 + z2 = 36

x ≥ 0

200

http://vk.com/studentu_tk, http://studentu.tk/

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 1920 / 2420 21 22 23 24 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
19.02.20169 Mб95Higher_Mathematics_Part_1.pdf
#
19.02.20166.63 Mб1052Higher_Mathematics_Part_1.pdf
#
19.02.20169.73 Mб45Higher_Mathematics_Part_2.pdf
#
19.02.20167.48 Mб408Higher_Mathematics_Part_2.pdf
#
19.02.20167.31 Mб123Higher_Mathematics_Part_2.pdf
#
19.02.20169.11 Mб304Higher_Mathematics_Part_3.pdf
#
19.02.2016694.82 Кб11HiraganaKatakanaWorkSheet (1).pdf
#
11.09.2019192.23 Кб1hjuj;f.docx
#
27.11.2019386.05 Кб9How Airplanes Work.doc
#
20.11.201958.78 Кб8I exercise 5.docx
#
19.02.201615.51 Mб28IFPS.pdf