Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный авиационный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Higher_Mathematics_Part_3

.pdf

Скачиваний:

304

Добавлен:

19.02.2016

Размер:

9.11 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 243 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 > Следующая >>>

			∞			2n
Example 14. Examine the series ∑								for convergence.
Example 14. Examine the series ∑					n			for convergence.
			n=1 ln			(n + 1)
Solution. We have an =		2n
				,
	lnn			,
	lnn	(n + 1)
lim n a		n	= lim			2	= 0		< 1.
lim n a			= lim				= 0		< 1.
n→∞			n→∞ ln(n + 1)
n→∞			n→∞ ln(n + 1)

By the Cauchy’s test, the series converges.

∞

)n2 for convergence.

Example 15. Examine the series ∑

n=1

Solution. Here a =

(1+

)n2 , n

a =

(1+

)n ,

lim n a

= lim

(1+

)n =

e > 1.

n→∞

n→∞ 2

By the Cauchy’s test, the series diverges.

∞

Example 16. Examine the series ∑

for convergence.

i=1 n

+ 1

Solution. Let’s consider Integral test. In this case f(x) =

. The integral

x2 + 1

+∞

∫

dx =

lim

∫

= lim arctan x

+ 1

b→ +∞

+ 1

b→ +∞

= lim (arctan b − arctan1)

= lim

−

arctan b −

b→ +∞

→ +∞

converges, and so does the series.

∞

Example 17. Examine the series ∑

for convergence.

i=1 n

+ 1

Solution. Since the nth term of the series is f (n) =

we choose the

n2 + 1

function f (x) =

which satisfies the conditions of the theorem, and then

x2 + 1

+∞

consider the improper integral

∫

dx.

1 x

http://vk.com/studentu_tk, http://studentu.tk/

We have

+∞

1 b

d (x

2 + 1)

∫

dx =

lim

∫

dx = lim

∫

+ 1

b→ +∞

+ 1

b→+∞ 2 1

lim ln(x2

+ 1)

lim (ln(b2

+ 1)

− ln 2) = +∞,

2 b→+∞

2 b→ +∞

which diverges, and so does the series. By the Integral test, the series diverges.

∞

Example 18. Examine the series ∑

for convergence.

i=1 (n − 2)ln

(n − 2)

Solution.

Since

the n-th

term

f (x) =

(n − 2) ln2 (n − 2)

will be, where

x ≥ 4.

(x − 2) ln2 (x − 2)

Then

+∞

∫

lim

∫

− 2) ln

− 2)

(x − 2) ln

(x −

b→ +∞

d (ln(x − 2)

= lim

∫

= lim

−

lim

−

(x − 2)

ln(x −

ln(b − 2)

ln 2

b→ +∞

b→+∞

+∞

Since the integral

∫

converges, so does the original series.

(x −

4 (x − 2) ln

Example 19. Examine for conditional convergence and absolute conver-

gence the series 1−

−

+ ... +

(−1)n−1

+ ... .

Solution. Let’s check up conditions of the Leibniz test.

1 >

> ...

lim a

= lim

= 0.

n→∞

n→∞ n

Then the given alternating series converges.

∞

Let’s consider the series in the form ∑

, i.e. 1

+ ... +

+ ... .

∞

n=1

This series diverges, because ∑

is the harmonic series.

n=1 n

Thus the given series is conditionally convergent.

http://vk.com/studentu_tk, http://studentu.tk/

Micromodule 1

CLASS AND HOME ASSIGMENTS

Write down the nth term of the series below:
a)	1+			1		+		1		+			1			+ ...			e)		2	+		6		+				24			+			120				...
								5					7							3			8
				3																								15						24
b)		1	+			1		+		1		+			1			+ ...	f)	2		+	4			+			6			+			8			+ ...
	2					4				6										5			8					11						14
													8
c)		1	+			8		+		27			+ ...						g) 1+				1 3				+				1 3 5						+		1 3 5 7				+ ...

	2					3		4															1 4							1 4 7								1 4 7 10
d)	1+				2		+		3		+			4			+ ...		h) 1+				1		+ 3 +							1		+ 5 +							1	+ ...
				2				4					8										2									4
																																						6

Find the sum Sn of the first n terms of the following series and prove its convergence using the definition of the convergence of a series.

∞

2n + 3n

∞

1. ∑

. 2. ∑

. 3. ∑

. 4. ∑ln 1

−

(2n − 1)(2n + 1)

n 1

n 1 n!(n + 2)

n 1

Examine the following series for divergence using the sufficient condition of the divergence.

∞

n + 2

∞

n − 2

∑

(n + 1)sin

∑

7. ∑

n 1

+ 1

n 1

+ 2n + 5

n 1

n + 3

∞

πn

∑

∑cos

10. ∑sin

6n + 5

n=2 ln n

n=1

Use the comparison test to examine the following series for convergence.

	∞	2n + 1								∞	n2 + n + 1									∞			1
11.	∑						.		12.	∑									.	13. ∑							.
11.	∑	3n	2		− 1		.		12.	∑	4n			5	+ 3				.	13. ∑							.
	n=1	3n			− 1					n=1	4n				+ 3					n=1 n2 + 1
	∞	2		n						∞				1						∞			π
14.	∑	2				.			15.	∑				1				.		16. ∑ tg			π					.
14.	∑					.			15.	∑								.		16. ∑ tg			3n +		2			.
	n=1	3n + 2								n=1 ln(n + 4)										n=1			3n +		2
	∞									∞						1				∞	3n + 4n
17.	∑ ( n + 1 − n).								18.	∑	1		− cos						.	19. ∑						.
17.	∑ ( n + 1 − n).								18.	∑	1		− cos				n		.	19. ∑	4	n	+ 5	n		.
	n 1									n 1							n			n 1	4		+ 5
	=									=		1								=
	∞ 4 n + 2											1
	∞ 4 n + 2									∞	e		n − 1							∞							1
20.	∑							.	21.	∑						.				22. ∑ n ln 1+										.
20.	∑							.	21.	∑			n			.				22. ∑ n ln 1+							n		2	.
	n=1	3 n5 + 1								n=1			n							n=1							n
																														23

http://vk.com/studentu_tk, http://studentu.tk/

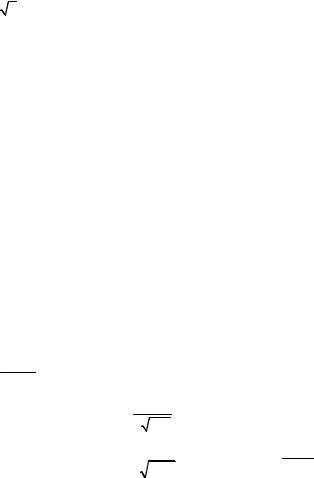
Using the D’Alembert’s test, examine the series for convergence.

∞

1 3 5 …(2n − 1)

23.

∑

n arctg

24. ∑

25. ∑

(n + 2)!

2 5 8 …(3n − 1)

n=1

∞

(2n + 1)!

∞

4n + 1

∞

(n!)

26.

∑

27. ∑

28. ∑ 2n sin

29. ∑

n 1 n3 7n+1

n 1

(2n)!

Using the Cauchy’s test, examine the series for convergence.

	∞	2n + 1		n
30.	∑			.
30.	∑			.
	n 1	5n + 3
	=
	∞		n		n
33.	∑ arccos					.
33.	∑ arccos				2n + 1	.
	n 1				2n + 1
	=

∞

n + 1 2n+3

∞

1 n

n + 2

31.

∑

. 32.

∑

n 1

∞

n2 + 1

∞

n + 1

34.

∑

35.

∑

n=1

Using the Integral test, examine the series for convergence.

	∞			1			∞	1				∞	ln n
36.	∑				.	37.	∑				.	38. ∑			.
36.	∑		2	+ 4	.	37.	∑	+ ln	2		.	38. ∑	n	2	.
	n=1 n			+ 4			n=2 n(1	+ ln		n)		n=1	n
	∞				1		∞	1
39.	∑					. 40.	∑					.
39.	∑	(2n + 1) ln(2n + 1)				. 40.	∑					.
	n=2	(2n + 1) ln(2n + 1)					n=2 n ln n ln ln n

Examine for conditional convergence and absolute convergence the series.

∞ cos πn

41. ∑ .

n=1 n + 1

∞	n	+ n
44. ∑(−1)n+1	3		.
	n	+ 1
n=1	4

∞		n
42. ∑ (−1)n+1			.
	n2
n=1		+ n + 1

∞(−1)n

45.∑ n ln n .n=2

∞

n 2n + 3

∞

(−1)n

47.

∑

(−1)

. 48.

∑

n 1

3n + 2

∞

sin 2

50.

∑

n=1

	∞			2n + 9
43.	∑	(−1)n+1		2n + 9			.
43.	∑	(−1)n+1					.
	n=1		11n − 3
	n=1
	∞		(−1)		n
46.	∑	2n tg	(−1)			.
46.	∑	2n tg	5n			.
	n=1		5n

∞(−3)n

49.∑ n! .n=1

Calculate approximately sum of series with accuracy ε . Indicate least sufficient of the members of a series.

∞	(−1)n+1				∞			2 n+1
51. ∑				, ε = 0,001.	52. ∑	−			, ε = 0,001.
51. ∑	n	3		, ε = 0,001.	52. ∑	−	13		, ε = 0,001.
n 1	n		n!		n 1		13
=					=

http://vk.com/studentu_tk, http://studentu.tk/

Answers

1. Sn =

−

, S =

. 2. Sn

−

, S =

4n + 2

2 3n

Hint. un =

n + 1

−

. 4.

Sn = ln

n + 1

n!(n + 2)

(n + 2)!

(n +

1)!

(n +

2)!

Sn = 1 −	1		,	S = 1.
	(n +	2)!

= − ln 2. 11. Diverges.

12. Converges. 13. Diverges. 14. Converges. 15. Diverges.16. Diverges. 17. Diverges. 18.Converges. 19. Converges. 20. Converges. 21. Converges. 22. Diverges. 23. Converges. 24. Converges. 25. Converges. 26. Diverges. 27. Converges. 28. Converges. 29. Converges. 30. Converges. 31. Converges. 32. Converges. 33. Diverges. 34. Converges. 35.Converges.36. Converges. 37. Converges. 38. Converges. 39. Diverges. 40. Diverges. 41.Conditionally converges. 42. Conditionally converges. 43. Diverges. 44. Absolutely converges. 45. Conditionally converges. 46. Absolutely converges. 47. Absolutely converges. 48. Absolutely converges. 49. Absolutely converges. 50. Absolutely converges. 51. S ≈ 0,944, n = 3 . 52. S ≈ 0,134, n = 3 .

Micromodule 1

SELF-TEST ASSIGNMENTS

1.1. Find the sum Sn of the first n terms of the following series and prove its convergence using the definition of the convergence of a series.

∞	3n + 4n
1.1.1. ∑		.
1.1.1. ∑	12n	.
n=1	12n
∞	1
1.1.3. ∑				.
1.1.3. ∑	(2n + 1)(2n + 3)			.
n=1	(2n + 1)(2n + 3)
∞	1
1.1.5. ∑			.
1.1.5. ∑	(n + 2)(n + 4)		.
n=1	(n + 2)(n + 4)
∞	4n − 3n
1.1.7. ∑		.
1.1.7. ∑	12n	.
n=1	12n

∞1

1.1.9.n∑=1 (n + 7)(n + 6) .

∞1

1.1.11.n∑=1 (n + 4)(n + 6) .

∞2n + 7n

1.1.13.∑ .n

n=1 14

∞1

1.1.15.n∑=1 (3n + 1)(3n + 4) .

∞

1.1.2. ∑

n=1 n(n +

∞

5n − 3n

1.1.4. ∑

15n

n=1

∞

5n − 2n

1.1.6. ∑

10n

n=1

∞

1.1.8. ∑

(2n +

5)(2n + 7)

n=1

∞

3n + 7n

1.1.10. ∑

21n

n=1

∞

5n − 3n

1.1.12. ∑

15n

n=1

∞

1.1.14. ∑

(n +

3)(n + 5)

n=1

∞

7n − 2n

1.1.16. ∑

n=1

http://vk.com/studentu_tk, http://studentu.tk/

∞			1
1.1.17. ∑								.
1.1.17. ∑	(n + 4)(n + 6)							.
n=1	(n + 4)(n + 6)
∞	6n − 5n
1.1.19. ∑					.
1.1.19. ∑		30n			.
n=1		30n
∞				1
1.1.21. ∑									.
1.1.21. ∑	(2n + 3)(2n +						5)		.
n=1	(2n + 3)(2n +						5)
∞				1
1.1.23. ∑									.
1.1.23. ∑	(2n + 3)(2n +						5)		.
n=1	(2n + 3)(2n +						5)
∞	2	n	+ 9	n
1.1.25. ∑	2		+ 9			.
1.1.25. ∑		18n				.
n=1		18n
∞			1
1.1.27. ∑							.
1.1.27. ∑	(n + 3)(n + 5)						.
n=1	(n + 3)(n + 5)
∞				1
1.1.29. ∑									.
1.1.29. ∑	(3n + 5)(3n +						2)		.
n=1	(3n + 5)(3n +						2)

∞	4n + 5n
1.1.18. ∑							.
1.1.18. ∑	20n						.
n=1	20n
∞					1
1.1.20. ∑										.
1.1.20. ∑	(2n −			1)(2n + 1)						.
n=1	(2n −			1)(2n + 1)
∞	n	+ 8			n
1.1.22. ∑	3	+ 8				.
1.1.22. ∑	24n					.
n=1	24n
∞	7n − 4n
1.1.24. ∑								.
1.1.24. ∑	28n							.
n=1	28n
∞					1
1.1.26. ∑										.
1.1.26. ∑	(3n −			1)(3n + 2)						.
n=1	(3n −			1)(3n + 2)
∞	10	n			n
1.1.28. ∑	10		− 3						.
1.1.28. ∑									.
n=1	30n
∞	9n − 2n
1.1.30. ∑							.
1.1.30. ∑	18n						.
n=1	18n

1.2. Examine the following series for divergence.

∞

1.2.1. ∑ cos

n=1

∞

n − 1 n

1.2.3. ∑

n 1

∞

ln n

1.2.5. ∑

+ 2 ln n

n=1 3

∞

2n − 1 n

1.2.7. ∑

n 1

∞

1.2.9. ∑ cos

n=1

∞

1.2.11. ∑ ( n2 + n + 1 − n) .

n=1

∞ln n

1.2.13.n∑=1 1+ 2 ln n .

∞7n − 1

1.2.2.n∑=1 1000n + 1 .

∞n2 + 1

1.2.4.n∑=1 5n2 − 3n + 1 .

∞n + 1 n2

1.2.6.∑ .

nn=1

∞3n + 5

1.2.8.n∑=1 5n + 1000 .

∞2n2 + 1

1.2.10.n∑=1 n(3n + 1) .

∞n!

1.2.12.n∑=1 n!+ 10 .

∞3 + n!

1.2.14.n∑=1 100 + n! .

http://vk.com/studentu_tk, http://studentu.tk/

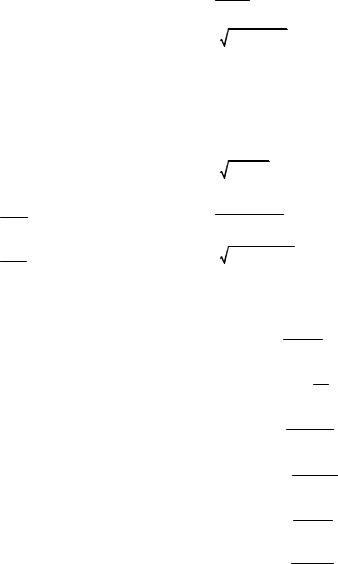
n=1

∞

1.3.12. ∑

n=1

∞

1.3.6. ∑

n=1

∞

1.3.9. ∑

∞

1.3.3. ∑

n=1

∞

1.2.15. ∑

(n + 3)!

n=1

∞

1.2.17. ∑ cos πn .

n=1

∞

n + 3

1.2.19. ∑

+ 2

n=1

∞

1.2.21. ∑ ctg

n=1

∞

2n − 5

1.2.23. ∑

n=1

100n + 3

∞

πn

1.2.25. ∑ arctg

n=1

6n + 1

∞n + 5 n

1.2.27.n∑=1 n + 4 .

∞n − 3 2n

1.2.29.n∑=1 n .

∞	3n − 5 n
1.2.16. ∑		.

n=1	3n

∞4n + 7

1.2.18.n∑=1 7n − 4 .

∞
1.2.20. ∑ (		n2 + 4n + 5 − n) .
n=1
∞		ln n
1.2.22. ∑		ln n			.
1.2.22. ∑	2	+ ln n			.
n=1	2	+ ln n
∞			n −	1
1.2.24. ∑ cos			n −	1		.
1.2.24. ∑ cos			2			.
n=1			n
∞
1.2.26. ∑ (		n2 + 2n − n) .

n=1

∞(n + 2)n

1.2.28.n∑=1 (n + 3)(n + 1) .

∞
1.2.30. ∑ ( 4n2 + 3n + 7	− 2n) .
n=1

1.3. Using the D’Alembert’s test, examine the series for convergence.

∞

(n + 2)!

∞

7n − 1

1.3.1. ∑

1.3.2. ∑

n=1

(n + 1)!

∞

+ 3

∞

4 5 6 (n+3)

1.3.4. ∑

1.3.5. ∑

n=1 n 3n−1

n=1 5 7 9 (2n+3)

∞

nn+1

∞ 1 7 13 (6n−5)

1.3.7. n∑=1

1.3.8. n∑=1

2 3 4 (n+1)

(n + 1)!

∞

(n + 2)!

∞

1.3.10. ∑

1.3.11. ∑(2n +1) tg

n=1

∞

1 6 11 (5n − 4)

1.3.13. ∑

1.3.14. ∑

(n +

3)!

n=1

3 7 11 (4n −1)

∞

2π

∞

+ 1) 2

1.3.16. ∑ n3 tg

1.3.17. ∑

n=1

(n + 1)!

(n + 3)! . n! 2n

n sin 2π . 3n

3n(n + 1) .

(n +1)n2 . n!

∞nn

1.3.15.n∑=1 (n + 3)! .

∞ln n

1.3.18.n∑=1 (2n + 3)! .

http://vk.com/studentu_tk, http://studentu.tk/

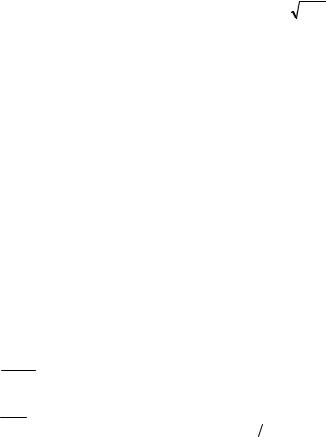
∞	2n (2n −1)
1.3.19. ∑							.
1.3.19. ∑		5n					.
n=1		5n
∞				π
1.3.22. ∑ n!sin				π		.
1.3.22. ∑ n!sin						.
n=1				2n
∞	5	n
1.3.25. ∑	5		.
1.3.25. ∑	4n!		.
n=1	4n!
∞	(2n −1)3
1.3.28. ∑					.
1.3.28. ∑					.
n=1	(2n)!

∞

3 5 8 (3n −1)

∞

(n +1)n

1.3.20. ∑

1.3.21. ∑

3 7 11 (4n −1)

n=1

n 1

∞

1 5 9 (4n − 3)

∞

(n!)2

1.3.23. ∑

1.3.24. ∑

1 4 7 (3n − 2)

(2n)!

n=1

∞ 1 3 5 (2n −1)

∞

1.3.26. n∑=1

1.3.27. n∑=1

2 7 12 (5n − 3)

(n + 1)!

∞

2n +1

1.3.29. ∑

(3n − 1) sin

1.3.30. ∑

n=1

n=1 n 2n

1.4. Using the Cauchy’s test, examine the series for convergence.

∞

1.4.1. ∑

n 1

n + 1

∞

1.4.3. ∑

arctg

n 1

2n + 1

∞

1.4.5. ∑

arcsin

n=1

∞

n+ 1.

1.4.7. ∑ arctg n 2

n =1

∞

2n +1

1.4.9. ∑

(n + 1)

n =1 ln

∞

πn

1.4.11. ∑ sin

+ 5

n =1

1.4.13. ∞ 2n − 1 n2 .

∑ n =1 2n

1.4.15. ∞ n + 1 n+1.

∑ n =1 4n

∞		1	n
1.4.17. ∑	e2n		− 1	(n
n=1
n=1

2 n .

+ 1)n .

∞

5n − 1 n2

1.4.2. ∑

n 1

∞

1.4.4. ∑

arctg

n 1

2n + 1

∞

n2 + 5n + 8

1.4.6.

∑

− 2

n=1

∞

1.4.8. ∑

n 1

n + 2

∞

1.4.10. ∑

n =1

∞

πn

1.4.12. ∑ tg

6n +

∞

π 2n

1.4.14. ∑

sin

n=1

∞

1.4.16. ∑

n =1 ((n + 1) n)n2

∞

3n − 1 n2

1.4.18. ∑

http://vk.com/studentu_tk, http://studentu.tk/

∞

5n + 2

1.4.19. ∑

(n +

n =1 ln

∞

3n2

− 1

1.4.21. ∑

+ 4

n=1

∞

πn

1.4.23. ∑ sin

n 1

4n +

∞

((n + 1)

n)n2

1.4.25. ∑

n =1

∞

n −

1.4.27. ∑

n 1

∞

1.4.29. ∑

1))n

n =1 (ln(n +

1.4.20. ∞ n + 1 n2 .

∑ n=1 2n

1.4.22. ∞ n n .

∑ n =1 3n + 1

∞	n + 1				5n
1.4.24. ∑				.
1.4.24. ∑		2n		.
n =1		2n
∞		1				n	(3n + 1)n .
1.4.26. ∑	e 4n		− 1				(3n + 1)n .
n=1
n=1

∞		3n
1.4.28. ∑ arctgn		3n	.
1.4.28. ∑ arctgn			.
n =1	n + 2
n =1
∞		n + 2
1.4.30. ∑ arcsin n		n + 2		.
1.4.30. ∑ arcsin n				.
n =1		2n
n =1

1.5. Use the comparison test to examine the following series for convergence.

∞

1.5.1. ∑

1.5.2. ∑

n=1 n3 + 2

n=1 3 n5 + n − 1

∞

n + 1

∞

1.5.3. ∑

1.5.4. ∑

+ 2

n=1

n=1 n3 + 3n

∞

1.5.5. ∑

1.5.6. ∑

n=1

n2 + n

n=1 ln(n +

∞

1.5.7. ∑

1.5.8. ∑

n=1

3 2n4 + 1

n=1 3n − 1

∞

n + 3

1.5.9. ∑ tg

1.5.10. ∑

4n −

n=1

n=1 n(n + 1)

∞

− 1

∞

cos

1.5.11. ∑

1.5.12. ∑

+ 1

n=1 n

+ 1

n=1

∞

2n − 1

∞

1.5.13. ∑

1.5.14. ∑

− n +

n=1

http://vk.com/studentu_tk, http://studentu.tk/

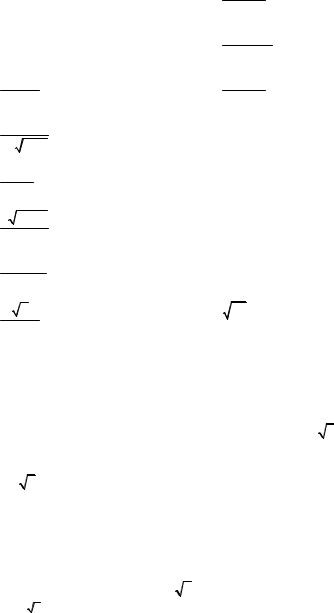
∞		π
1.5.15. ∑ n sin					.
		n2
n=1			+ 1
∞		2π
1.5.17. ∑ sin				.
	3n +		2
n=1

∞3n − 1

1.5.19.n∑=1 2n2 − 1 .

∞n + 2

1.5.21.n∑=1 n 3 n + 1 .

∞n2

1.5.23.n∑=1 n3 + 2 .

∞n 2n + 1

1.5.25.∑ .

+1n=1 n3

∞1

1.5.27.n∑=1 ln(n + 4) .

∞n

1.5.29.n∑=1 5n2 + 3 .

∞n + 2

1.5.16.n∑=1 n(n + 4) .

∞5n + 1

1.5.18.n∑=1 n3 + n + 1 .

∞n + 4

1.5.20.∑ .

n=1 n(n − 4)

∞					π
1.5.22. ∑ sin									.
1.5.22. ∑ sin			2n − 1						.
n=1			2n − 1
n=1
∞			π
1.5.24. ∑ sin			π			.
1.5.24. ∑ sin						.
n=1			4n
n=1
∞		1
1.5.26. ∑		1			.
1.5.26. ∑		2 n			.
n=1 n		5
∞	2n + 1
1.5.28. ∑							.
1.5.28. ∑		2	+	4			.
n=1 n			+	4
∞	3	n	2	+ 2
1.5.30. ∑		n		+ 2				.
1.5.30. ∑								.
n=1	n(n + 1)

1.6. Use the comparison test in limited form to examine the following series for convergence.

∞

1.6.1. ∑ sin

1.6.2. ∑ ln 1

1.6.3. ∑

− cos

n + 2

n=1

∞

∞ 1

∞

n2 + 1

1.6.4.

1.6.5.

− 1 .

1.6.6.

∑ n

∑

n=1

∞

− 1

1.6.7. ∑ arcsin

1.6.8. ∑ sin

1.6.9. ∑

+ 1

n +

n=1

n=1 tg

∞

1.6.10.

+ 3

∑

− cos

1.6.11.

∑

arctg

1.6.12.

∑

+ 2

n=1

http://vk.com/studentu_tk, http://studentu.tk/

<<< < Предыдущая 1 23 / 243 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
19.02.20169 Mб95Higher_Mathematics_Part_1.pdf
#
19.02.20166.63 Mб1052Higher_Mathematics_Part_1.pdf
#
19.02.20169.73 Mб45Higher_Mathematics_Part_2.pdf
#
19.02.20167.48 Mб408Higher_Mathematics_Part_2.pdf
#
19.02.20167.31 Mб123Higher_Mathematics_Part_2.pdf
#
19.02.20169.11 Mб304Higher_Mathematics_Part_3.pdf
#
19.02.2016694.82 Кб11HiraganaKatakanaWorkSheet (1).pdf
#
11.09.2019192.23 Кб1hjuj;f.docx
#
27.11.2019386.05 Кб9How Airplanes Work.doc
#
20.11.201958.78 Кб8I exercise 5.docx
#
19.02.201615.51 Mб28IFPS.pdf