Higher_Mathematics_Part_3
.pdf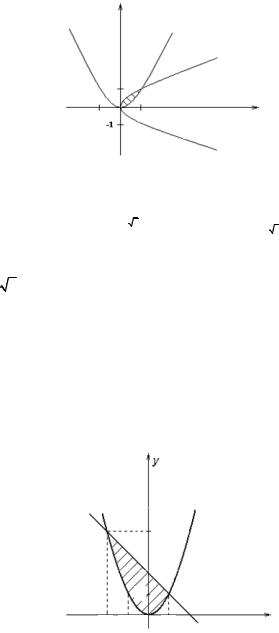
y
|
|
|
|
|
|
|
y = x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
– 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
||
|
|
– 1 |
|
|
|
|
|
|
|
x = y2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
Fig. 5.10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Therefore, we can apply here (5.20) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
1 |
|
|
|
x |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
∫∫(x + 2y)dxdy = ∫ dx ∫ (x + 2 y)dy = ∫(xy + y2 ) |
|
x2x dx = |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||
D |
|
0 x2 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1 |
|
5 |
|
|
|
2 |
|
|
4 |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
x2 |
|
|
x |
|
x |
|
x |
|
|
|
|
|
2 |
|
1 |
|
1 |
|
1 |
|
9 |
|
|||||||
= ∫(x x + x − x3 − x4 )dx = ( |
|
+ |
|
− |
|
− |
|
|
) |
|
10 |
= |
+ |
− |
− |
= |
. |
|||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
0 |
5 |
2 |
4 |
5 |
|
|
|
|
5 |
|
2 |
4 |
|
5 |
|
20 |
|
|||||||||||||||
|
2 |
|
|
|
|
|
|
|
I = ∫∫(x + 2y)dxdy |
|
|
|
|
|
||||||||||||||||||
Example 2. We take the double integral |
|
over a domain |
||||||||||||||||||||||||||||||
|
y = 2 − x and y = x2 . |
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
D bounded by the lines |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
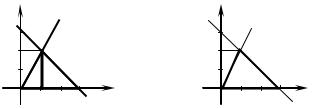
Solution. Our domain is regular in both directions (Fig. 5.11). Let’s find coordinates of intersection points of parabola y = x2 and straight lines y = 2 − x.
We have x2 = 2 − x, |
then x2 + x − 2 = 0. We obtain x |
= −2, x = 1. |
|||
|
|
1 |
2 |
||
y = 2 – x |
y |
|
y = x2 |
|
|
|
|
||||
|
|
|
|||
|
|
|
|||
4 |
|
||||
|
|
|
|||
|
|
1 |
|
|
|
|
|
–2 –1 O 1 |
y |
||
|
|
Fig. 5.11 |
|
||
111
http://vk.com/studentu_tk, http://studentu.tk/
We obtain
|
|
|
|
|
|
|
1 |
2− x |
|
|
|
|
|
1 |
|
|
2− x |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
I = ∫∫ (x + 2y)dxdy = ∫ dx ∫ |
(x + 2y)dy = ∫ dx(xy + y2 ) |
= |
|||||||||||||||||
|
1 |
D |
|
|
|
|
|
|
−2 |
x2 |
|
|
|
|
1 |
−2 |
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4 − 2x − x3 − x4 )dx = |
|||||
= ∫ |
(x(2 − x) + (2 − x)2 − x3 − x4 )dx = ∫ |
||||||||||||||||||
|
−2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
−2 |
|
|
|
|
|
4x |
− x2 |
|
x4 |
|
x5 |
|
|
1 |
|
|
1 |
|
1 |
− |
|
32 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
= |
− |
|
− |
|
|
|
|
= 4 − 1− |
|
− |
|
−8 − 4 − 4 + |
|
= 12,15. |
|||||
|
|
|
|
|
|||||||||||||||
|
|
|
|
4 |
|
5 |
|
|
−2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 5 |
|
5 |
|
|||||||
Example 3. Let’s change the order of integration. We preliminarily draw the
domain of integration: ∫∫ f (x, |
y)dxdy |
over the domain D bounded by the lines |
|||||||
|
|
D |
|
|
|
|
|
|
|
y = 2x, x + y = 3, y = |
0 . |
|
|
|
|
|
|
||
Solution. Examine D. The straight lines |
y = 2x |
and |
y = 3 − x |
meet at point |
|||||
A(1, 2). Domain D is a triangle (Fig. 5.12). |
|
|
|
|
|||||
1. This domain is regular. So, y |
varies from 0 to 2, and ϕ1 (x) = 2x and |
||||||||
ϕ2 (x) = 3 − x. |
Any straight line y = const, (0 ≤ y ≤ 2) |
meets the boundary of |
|||||||
the region at not more than two points. |
|
|
|
|
|
||||
Therefore, we can apply here |
|
|
|
|
|
||||
|
|
∫∫ f (x, |
|
2 |
3− x |
|
|
|
|
|
|
y)dxdy = ∫ dy ∫ f (x, |
y)dy. |
|
|||||
|
|
D |
|
|
0 |
2x |
|
|
|
y |
|
|
|
|
|
y |
|
|
|
3 |
|
y = 2x |
|
|
3 |
|
|
|
|
|
А |
|
|
|
|
А |
|
||
2 |
|
|
|
|
2 |
|
|
||
|
y = 3 – x |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
О |
|
|
В |
x |
|
О |
|
В |
x |
1 |
3 |
|
1 |
3 |
|||||
|
|
а |
|
|
|
|
|
b |
|
|
|
|
|
Fig. 5.12 |
|
|
|
||
2. Let’s change the order of the integration. The domain should be broken into two parts, each of which will be regular: if 0 ≤ x ≤ 1, then 0 ≤ y ≤ 2x ; if
1 ≤ x ≤ 3 , then 0 ≤ y ≤ 3 − x . We obtain
∫∫ f (x, |
1 |
2 x |
3 |
3− x |
y)dxdy = ∫ dx ∫ |
f (x, y)dy + ∫ dx ∫ f (x, y)dy. |
|||
D |
0 |
0 |
1 |
0 |
112
http://vk.com/studentu_tk, http://studentu.tk/

Example 4. Take the double integral ∫∫ f (x, y)dxdy, if
D
f (x, y) = x + 2y over a domain D is bounded by the lines
x = 0, y = |
x |
and y = 5 − x2 . |
|
|
|
|
|
||
|
|
|
|
|
|
||||
2 |
|
|
|
|
|
|
|
|
|
Solution. We have the domain D bounded by straight |
|||||||||
lines x = 0, |
y = |
x |
and the parabola |
y = 5 − x2 (Fig. 5.13). |
|||||
|
|||||||||
|
|
2 |
|
x |
|
|
|
|
|
x varies from 0 to 2, and ϕ (x) = |
and ϕ |
|
(x) = 5 − x2 . |
||||||
|
2 |
||||||||
|
|
1 |
2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
y
5
y = 5 – x2
D |
х = 2у |
|
1
О 2 x
Fig. 5.13
|
|
|
|
|
|
|
|
|
2 |
|
5− x2 |
|
|
2 |
|
|
|
|
|
y |
2 |
|
|
5− x2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Therefore ∫∫ f (x, |
y)dxdy = ∫ dx ∫ |
(x + 2 y)dy = ∫(xy + 2 |
|
|
|
) |
|
dx = |
||||||||||||||||||||||||||
|
2 |
|
||||||||||||||||||||||||||||||||
|
|
D |
|
|
|
|
|
0 |
|
|
|
x |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
x |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||
2 |
|
|
|
|
|
|
|
|
|
x |
2 |
|
|
x |
2 |
|
|
|
2 |
|
|
|
43 |
|
|
|
|
|
|
|
|
|||
= ∫(x(5 − x2 ) + (5 |
− x2 )2 − |
|
|
− |
|
|
)dx = ∫(x4 − x3 − |
x2 |
+ |
5x + 25)dx = |
||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
2 |
|
4 |
|
|
|
|
0 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|||||
x5 |
|
|
x4 |
|
|
43x3 |
|
5x2 |
|
|
|
|
|
|
|
2 |
|
25 |
|
86 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
= |
|
|
− |
|
− |
|
|
+ |
|
|
|
|
+ 25x |
|
|
= |
|
− 4 − |
|
|
+ 10 |
+ 50 ≈ 34. |
||||||||||||
|
|
4 |
12 |
2 |
|
5 |
3 |
|
||||||||||||||||||||||||||
5 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
For the replacement of integration order we shall construct area D on Оy, and receive a segment [0,5] . As the regular boundary of the domain consists of two
different lines, then we shall divide this domain into two parts by line |
y = 1. |
||||||||||||||
Defined from the equations |
|
|
y = |
x |
and |
y = 5 − x2 |
a variable y through |
x, we |
|||||||
|
|||||||||||||||
shall receive |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 y |
|
5 |
|
|
5− y |
|
||||
∫∫ f (x, y)dxdy = ∫ dy ∫ (x + 2 y)dx + ∫ dy ∫ (x + 2 y)dx = |
|
||||||||||||||
D |
|
|
0 |
0 |
|
|
1 |
|
|
0 |
|
||||
1 x2 |
|
|
|
2 y |
|
|
5 x2 |
|
|
|
5− y |
|
|||
|
|
|
|
|
|
||||||||||
= ∫ |
|
+ 2yx |
|
|
|
dy + ∫ |
|
|
+ 2 yx |
|
|
dy ≈ −21.56. |
|
||
2 |
|
2 |
|
||||||||||||
0 |
|
|
|
0 |
|
|
0 |
|
|
0 |
|
|
|||
|
|
|
|
|
|
|
|
|
|||||||
Example 5. Calculate the integral |
∫∫(6x − 3y)dxdy, where D :{x + y = 1, |
||||||||||||||
D
x + y = 2, 2x − y = 1, 2x − y = 3}.
Solution. Let’s construct the given domain D which is bounded by straight lines y = 1− x, y = 2 − x, y = 1+ 2x, y = 3 + 2x (Fig. 5.14).
113
http://vk.com/studentu_tk, http://studentu.tk/
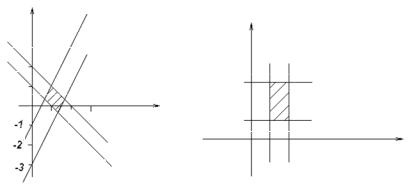
We substitute
x + y = u, 2x − y = v.
Therefore all equations of the straight lines can be written as
x + y = 1 into u = 1, x + y = 2 into u = 2, 2x − y = 1 into v = 1, 2x − y = 3 into v = 3.
Let’s construct the domain |
D* : |
{ |
} |
in uv-plane (Fig. 5.15). |
|
u = 1, u = 2, v = 1, v = 3 |
Further for a determination of a Jacobian, it is necessary to transform it so that to receive x and y through u and v. We have
|
|
|
|
x = |
1 |
(u + v) |
|||
|
|
3x = u + v |
|
|
|
|
|||
3 |
|||||||||
x + y = u |
|
|
|
||||||
|
|
|
|
|
1 |
|
|
||
2x − y = v |
2x − y = v |
|
|
|
|
||||
|
|
|
y = |
|
|
(2u − v) |
|||
|
3 |
||||||||
|
|
|
|
|
|
|
|||
|
∂x |
Now we find partial derivatives of the first order with respect to u and v, |
||||||||||||||||||||||||||||||||
|
= |
|
1 |
, |
∂x = |
1 |
, |
∂y |
= |
2 |
, |
∂y |
= − |
1 |
|
. Then Jacobian equals |
||||||||||||||||||
|
|
|
|
|
|
|
|
∂v |
|
|||||||||||||||||||||||||
|
∂u 3 |
∂v 3 |
∂u 3 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
I (u,v) = |
|
∂x |
|
∂x |
|
|
|
1 |
|
1 |
|
|
|
= − |
1 |
− |
2 |
|
1 |
≠ 0 . |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
∂u |
∂v |
= |
|
3 |
3 |
|
|
= − |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂y |
|
∂y |
|
|
|
2 |
− |
1 |
|
|
9 |
9 |
|
3 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂u |
|
∂v |
|
|
|
3 |
3 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
V |
|
|
|
2x – y = 1 |
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
2 |
|
|
|
|
2x – y = 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v = 3 |
||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
O |
1 |
2 |
3 |
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v = 1 |
|||
|
|
|
|
– 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
x + y = 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
– 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O |
1 |
2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
– 3 |
|
|
x + y = 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
Fig. 5.14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fig. 5.15 |
|||||||||
114 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
http://vk.com/studentu_tk, http://studentu.tk/
We obtain |
|
I (ρ, ϕ) |
|
= |
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Now the given integral is equal to |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
∫∫(6x − 3y)dxdy = ∫∫[6 |
1 |
(u + v) |
− |
3 |
1 |
(2u − v)] |
|
1 |
dudv = |
|||||||||||||||||||
3 |
|
3 |
||||||||||||||||||||||||||
D |
|
|
|
|
|
|
|
D* |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|||||
|
1 |
|
|
|
2 |
3 |
|
2 |
v |
2 |
|
|
|
|
|
|
2 |
9 |
|
|
|
1 |
|
|
||||
= |
∫∫3vdudv =∫ du∫vdv = ∫ |
|
|
|
|
13 |
du = ∫( |
|
− |
|
)du = 4. |
|||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||
3 |
2 |
|
2 |
|
|
2 |
||||||||||||||||||||||
|
* |
|
|
1 |
1 |
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|||||||||
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Example 6. Take the |
∫∫ |
1 |
|
|
dxdy |
|
|
|
where D : |
{ |
x2 + y2 ≤ 1, x ≥ 0, y ≥ 0 |
|||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
x2 + y2 |
|
|
|
|
|
|
|
|
|
|
|
|
} |
|||||||||
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
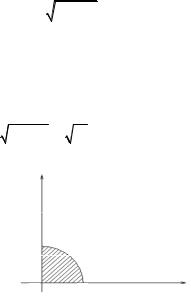
is the quarter of the unit circle in the first quadrant.
Solution. Let’s consider a domain D (Fig. 5.16). We pass to polar coordinates
x = ρ cos ϕ and y = ρ sin ϕ, |
then |
D |
* |
= |
|
|
≤ ρ ≤ 1; 0 |
≤ ϕ ≤ |
π |
and our integrable |
|||||
|
0 |
2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
function f (x, y) = |
1 |
|
= |
|
1 |
|
= |
1 |
, |
then the given |
integral can be |
||||
|
|
|
ρ2 |
|
ρ |
||||||||||
|
x2 + y2 |
|
|
|
|
|
|
|
|
||||||
transformed into
y
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
O |
|
1 |
|
|
x |
|
|
|
|
|
|
|
|
|
Fig. 5.16 |
|
|
|
|
|
|||
|
1 |
|
π |
π |
π |
|
|
π |
|
|||
|
|
|
|
|
|
|
|
π . |
||||
∫∫ |
ρdρdϕ = ∫02 dϕ∫01 dρ = ∫2 ρ |
|
10 dϕ = ∫2 1dϕ = ϕ |
|
|
02 = |
||||||
|
|
|||||||||||
|
||||||||||||
|
|
|
2 |
|||||||||
D* ρ |
|
|
0 |
|
|
0 |
|
|
|
|||
Example 7. Find the area S if D: x = y2 − 2 y, x − y = 0. |
|
|
|
|
||||||||
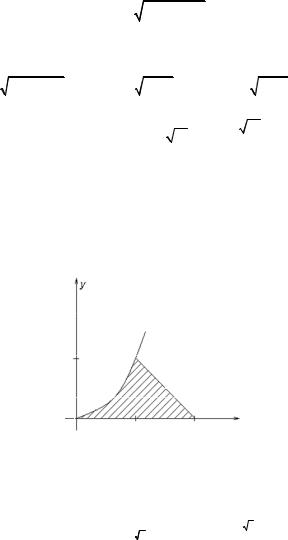
Solution. We write the given equation of |
x = y2 − 2 y |
in canonical form, |
||||||||||
y2 − 2y + 1−1 = x, then we have ( y − 1)2 = x + 1 . It is parabola with centre in the point A(–1; 1). Second equation x − y = 0 is a straight line (Fig. 5.17).
115
http://vk.com/studentu_tk, http://studentu.tk/

y
|
|
|
|
|
|
|
|
y = x |
|
|
|
|||||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–1 O |
1 2 |
3 |
|
|
|
|
|
|
|
|
|
x |
|||
|
|
–1 |
|
|
x = y2 – 2y |
|
|
|
||||||||
Hence |
|
|
Fig. 5.17 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
y |
3 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
S = ∫∫ dxdy = ∫ dy |
∫ |
dx = ∫ x |
|
|
|
dy = ∫( y − ( y2 − 2y))dy = |
||||||||||
|
|
|
||||||||||||||
D |
0 |
y2 − 2 y |
0 |
|
y2 − 2 y |
|
|
0 |
|
|
|
|
|
|||
|
3 |
|
|
3y |
2 |
|
y |
3 |
|
|
|
|
|
9 |
|
|
|
= ∫(3y − y2 )dy = ( |
|
− |
|
) |
|
|
30 |
= |
. |
||||||
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
||||||||||
|
0 |
|
|
2 |
|
3 |
|
|
|
|
2 |
|
||||
Example 8. Find the area S if D: x2 + y2 |
= 4x, |
y = x, y = 0. |
||||||||||||||
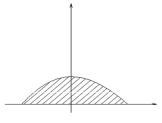
Solution. We construct the given figure (Fig. 5.18). The equation x2 + y2 = 4x is a circle of radius 2 with the centre at the point A(2; 0). Let’s find perfect square with respect to x, we obtain
x2 − 4x + y2 = 0, (x2 − 4x + 4) + y2 = 4, (x − 2)2 + y2 = 4.
The graph of the equations y = x and y = 0 are straight lines. They together
with the arc of a circle determine the domain D, which is a curvilinear sector with a top in the origin of coordinates.
y |
|
y = x |
|
|
C |
|
|
|
|
|
|
|
|
ρ = 4cosφ |
|
|
D |
|
|
O |
π/4 |
B |
x |
A(2; 0) |
Fig. 5.18
Taking into account the form of the domain, we shall calculate a double integral in a polar system.
116
http://vk.com/studentu_tk, http://studentu.tk/

In polar coordinates the equation of the circle can be written as
|
|
ρ2 cos2 ϕ + ρ2 sin2 ϕ = 4ρ cosρ, |
ρ2 |
= 4ρ cosρ, |
ρ = 4cos ϕ . |
||||||||||||||
|
Straight lines |
y = 0 and y = x in the polar components have the form ϕ = 0 |
|||||||||||||||||
and |
ϕ = π |
correspondently. Hence, polar components ϕ and ρ of the points which |
|||||||||||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π , |
|
|
|
belong to the domain, are changed within the limits: 0 ≤ ϕ ≤ |
0 ≤ ρ ≤ 4cos ϕ. |
||||||||||||||||||
|
We have |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
π |
4cos ϕ |
π |
ρ2 |
|
4cos ϕ dϕ = |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
S = ∫∫ dxdy = ∫∫ρdρdϕ = ∫4 dϕ ∫ |
ρ dρ = ∫4 |
|
|||||||||||||||
|
|
|
|
D |
|
D |
0 |
0 |
|
|
0 |
|
2 |
|
0 |
|
|
|
|
|
π |
|
|
|
π |
1 |
|
|
sin 2ϕ |
|
|
π |
|
|
π |
|
|
|
|
|
|
|
|
1+ cos 2ϕ |
|
|
|
|
|
|
1 |
||||||||
|
4 |
|
|
|
4 |
|
|
|
|
|
|
||||||||
|
|
2 |
|
|
|
|
4 |
|
|
|
|||||||||
|
= 8∫cos |
|
ϕdϕ = 8∫ |
|
dϕ = 4 |
ϕ + |
|
|
|
|
|
= 4 |
+ |
|
= π + 2. |
||||
|
|
2 |
|
|
|
|
2 |
||||||||||||
|
0 |
|
|
|
0 |
|
|
2 |
|
0 |
|
|
4 |
|
|
||||
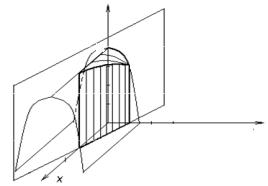
Example 9. Find the volume V bounded by a parabolic cylinder y = x2 and planes z = 0, z = 2 – y.
Solution. Examine D. Let’s consider a projection of the given figure on the xy-plane. We obtain:
− 2 ≤ x ≤ 2
and x2 ≤ y ≤ 2.
From Fig. 5.19 it is clear that the figure bounded from above by the plane z = 2 – y. Therefore,
|
|
|
|
2 |
2 |
|
|
|
|
2 |
|
|
|
|
|
y |
2 |
|
|
|
|
|
|
V = ∫∫(2 − y)dxdy = ∫ |
dx ∫ (2 − y)dy = |
|
∫ |
(2y − |
|
|
) |
|
2x2 dx = |
||||||||||||||
|
|
|
|||||||||||||||||||||
|
|
|
|||||||||||||||||||||
D |
|
|
− 2 |
x2 |
|
|
|
|
− 2 |
|
|
|
2 |
|
|
|
|
|
|||||
2 |
2 |
|
x4 |
|
|
|
|
2x3 |
|
|
x5 |
|
2 |
|
|
|
32 2 |
|
|||||
= ∫ (2 − 2x |
+ |
)dx = |
2x − |
+ |
|
|
2 = |
. |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
2 |
3 |
10 |
|
|
− |
15 |
||||||||||||||||
− 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
z 
2
O |
y |
2 |
x

Fig. 5.19
117
http://vk.com/studentu_tk, http://studentu.tk/