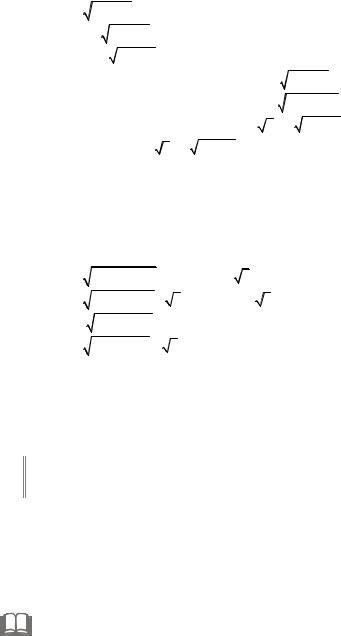
6.2.14. |
x = y2 + z2 , 3x = 18 − y2 − z2 . |
|
|
6.2.15. |
z = 6 − |
x2 |
+ y2 |
, |
z = x2 + y2 . |
|
|
6.2.16. |
y = 4 − 3 x2 + z2 |
, y = x2 + z2 . |
|
|
6.2.17. |
x2 + y2 + z2 |
= 1 , |
|
x2 + y2 + z2 |
= 16 , |
z = |
x2 + y2 ( x ≥ 0 ). |
6.2.18. |
x2 + y2 + z2 |
= 9 , |
x2 + y2 + z2 |
= 25 , |
z = |
3(x2 + y2 ) . |
6.2.19. |
x2 |
+ y2 |
+ z2 |
= 4 , |
|
x2 + y2 + z2 |
= 25 , |
3y = x2 + z2 . |
6.2.20. |
x2 |
+ y2 |
+ z2 |
= 4 , |
|
3y = x2 + z2 . |
|
|
6.2.21.x2 + y2 = 4 , z = 1, z = x + 2 y + 6 .
6.2.22.x2 + y2 = 9 , z = x2 + y2 + 4 , z = 0 .
6.2.23.x2 + z2 = 1, y = −1 , y = 10 − x2 − z2 .
6.2.24.x2 + y2 = 2x , z = 0 , z = x + y + 5 .
6.2.25.x2 + y2 = 4y , z = 0 , z = 2x + y + 6 .
6.2.26. |
z = |
25 − x2 − y2 , |
y = − x, y = |
3x |
( y ≥ 0). |
6.2.27. |
z = |
16 − x2 − y2 , |
3x − y = 0, |
x − |
3y = 0 (x ≥ 0, y ≥ 0). |
6.2.28. |
z = |
4 − x2 − y2 , |
y = x, y = 0 |
(x ≥ 0, y ≥ 0). |
6.2.29. |
z = |
9 − x2 − y2 , |
3x − y = 0, |
y = x |
(x ≥ 0, y ≥ 0). |
6.2.30. |
x2 + y2 + z2 = 4 , x2 + y2 + z2 = 4z. |
|
Micromodule 7
BASIC THEORETICAL INFORMATION. LINE INTEGRALS
Line integrals of the first and second type. Properties and evaluation. Green’s formula. Conditions for a line integral being pathindependent. Integration of total differentials. Application.
Key words: a line integral of the first type — криволінійний інтеграл першого роду, smooth — гладкий, piecewise smooth — кусково-гладкий, path-independent — незалежний від шляху, simple connected — однозв’язний, doubly connected — двозв’язний, triply connected — тризв’язний, spatial — просторовий, directrix — напрямна, generatrix — твірна, homogeneous — однорідний.
Literature: [3, part 2, item 2.4], [9, part 10, § 3], [15, part 12, item 12.3], [16, part 15, § 1—4], [17, part 3, § 9—10].
151
http://vk.com/studentu_tk, http://studentu.tk/

7.1. Line Integrals of the First Type. Basic Concepts
A line integral is generalization of a definite integral in the case when any curve is a domain of integration.
Let a smooth or piecewise smooth curve L bounded by points A and B (Fig. 7.1) be given in the plane Оху, and a continuous function z = f (x, y) be determined
on this curve. It should be reminded that a continuous curve x = x(t), y = y(t) is called smooth on a definite interval if functions x = x(t), y = y(t) have continuous, simultaneously not equal to zero derivatives x′(t) and y′(t) on this
interval. A continuous curve consisting of a finite number of smooth curves is called piecewise smooth.
|
y |
L |
An–1 Мn |
|
Мi |
|
В=An |
|
Ai–1 |
Ai |
|
A1 |
|
|
|
|
|
М1 |
|
|
|
А = A0 |
|
x |
|
О |
|
Fig. 7.1
We break up the arc AB into п some parts by points |
А = A0, А1, А2, ..., Ап |
= В, and designate |
by lk the length of the |
|
|
|
|
|
arc Ak −1 Ak ( k = 1, 2, …, n ). On each arc |
Ak −1 Ak |
|
we have to choose a point |
|
n |
|
|
|
Мk(хk, уk) and form the sum |
Sn = ∑ f (xk , |
yk ) lk , |
called the integral sum for |
|
k =1 |
|
lk |
|
the function f (x, y) on the arc АВ. Let λ = max |
be the length of the longest |
|
|
1≤k ≤n |
|
|
|
|
|
|
elementary arc Ak −1 Ak . |
|
|
|
|
Definition. If for λ → 0 |
the integral sum Sn |
has a finite limit which does |
not depend on the way of splitting the curve AВ by points Ak |
on parts, and the |
choice of points Mk, then this limit is called a line integral of the first type (or a |
line integral with respect to arc length) of the function f (x, y) |
over the curve |
АВ. It is designated as |
∫ f (x, y)dl. |
|
|
|
AB |
|
|
|
So, by definition |
∫ |
n |
|
(7.1) |
f (x, y)dl = lim ∑ f (xk , yk ) lk . |
|
|
AB |
λ→0 k =1 |
|
|
152 |
|
|
|
|
http://vk.com/studentu_tk, http://studentu.tk/
f(x, y)
If the limit (7.1) exists, the function f (x, y) is called integrated over the
curve АВ, the curve АВ is a path or a contour of integration, the point A is called the initial point, and B is called the terminal point of the path of integration.
Theorem If a function f (x, y) is continuous over a smooth curve АВ then a line integral of the first type ∫ f (x, y)dl exists.
AB
Properties of a line integral of the first type are similar to corresponding properties of a definite integral (formulate them yourselves). However there is one property which essentially differs from the corresponding property of the definite integral.
The line integral of the first type does not de-
pend on the direction of integration over the con- z tour АВ, i.e.
|
∫ f (x, y)dl = ∫ f (x, y)dl |
|
О |
|
|
AB |
BA |
|
y |
|
b |
a |
|
|
|
|
|
M(x, y) В |
whereas |
∫ f (x)dx = −∫ f (x)dx. |
x |
А |
|
a |
b |
|
|
|
Limits of integration in a line integral of the first |
Fig. 7.2 |
type must always be taken from the smaller to the |
|
greater. |
|
The geometrical significance of a line integral of the first type.
The line integral of the first type ∫ f (x, y)dl , where f (x, y) ≥ 0 ,
AB
numerically is equal to the area of a part of cylindrical surface whose directrix АВ lies in the plane Оху and generatrices are parallel to the axis Оz, provided
the cylindrical surface is bounded from above by the surface z = f (x, y) , from below by the plane Оху (Fig. 7.2).
7.2. Evaluation of a Line Integral of the First Type
Evaluation of a line integral of the first type is reduced to evaluation of a definite integral. We shall formulate rules of its evaluation in cases when the curve of integration is given by an explicit equation, in parametric form and in polar coordinates.
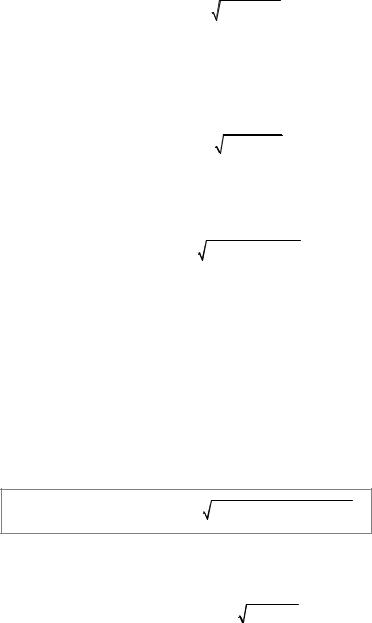
1. If the path АВ is given by the equation y = y(x) , x [а; b] (a is the
abscissa of the point A, b is the abscissa of the point В) where the functions y(x) and y′(x) are continuous in the segment [a; b], and the function f (x, y)
is continuous at each point of the path АВ, then
153
http://vk.com/studentu_tk, http://studentu.tk/
|
|
b |
|
|
|
|
|
|
∫ f (x, y)dl = ∫ f (x, |
′ |
2 |
dx. |
|
(7.2) |
|
y(x)) 1+ ( y (x)) |
|
|
|
AB |
a |
|
|
|
|
|
If the curve АВ is given |
by the |
equation x = x( y) , y [с; |
d] (c is the |
ordinate of the point A, d is the ordinate of the point В) where functions x( y)
and x′( y) are continuous in the segment [с; d], and the function |
f (x, y) |
is |
continuous at each point of АВ, then |
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
∫ f (x, y)dl = ∫ f (x( y), |
y) |
|
1+ (x′( y))2 dy. |
|
|
(7.3) |
|
|
AB |
c |
|
|
|
|
|
|
|
|
|
|
II. If the curve АВis given by parametric equations x = x(t), |
y = y(t) , t [α, |
β] |
and the functions |
x(t) , y(t) , |
x′(t) and y′(t) |
are continuous in [α, β] , then |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
β |
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
f (x, y)dl = ∫ |
f (x(t), y(t)) |
|
′ |
|
2 |
′ |
2 |
dt, |
|
(7.4) |
|
(x (t)) |
|
+ ( y (t)) |
|
|
|
AB |
α |
|
|
|
|
|
|
|
|
|
|
|
where the value of the parameter α corresponds to the point A, and β to the point B and the function f (x, y) is continuous over the path АВ.
Remark. A line integral of the first type of a function f (x, y, z) over a
spatial curve АВ is defined analogously with a line integral of the first type of a function f (x, y) .
Let the function f (x, |
y, z) be determined and continuous over the space |
piecewise smooth curve |
АВ given by equations x = x(t), |
y = y(t), z = z(t), |
t [α, β] . Then there exists a line integral ∫ f (x, y, z)dl |
evaluated by the |
formula |
AB |
|
|
|
β
∫ f (x, y, z)dl = ∫ f (x(t), y(t), z(t)) (x′(t))2 + ( y′(t))2 + (z′(t))2 dt.
AB α
IІI. If a plane curve АВ is given by the equation ρ = ρ(ϕ) ( α ≤ ϕ ≤ β ) in polar coordinates, then
|
∫ |
β |
|
f (x, y)dl = ∫ f (ρ cos ϕ, ρ sin ϕ) ρ2 + (ρ′)2 dϕ. |
|
AB |
α |
154 |
|
|
http://vk.com/studentu_tk, http://studentu.tk/
7.3. Line Integrals of the Second Type. Basic Concepts
Let functions of two variables P(x, y) and Q(x, y) be determined and
continuous at points of the arc АВ of a smooth curve L. Unlike integrals of the first type we shall consider a curve as a directed line, for which the points A and B are respectively initial and terminal points of the arc АВ. We break up the arc АВ into n arbitrary parts by points
А =A0, А1, А2, ..., Ап = В.
|
|
|
|
|
|
We take an |
arbitrary point |
Mi (xi , yi ) |
in each |
partial arc |
Ai−1 Ai |
( i = 1, 2, …, n ), |
calculate values |
of functions |
P(Mi ) |
and Q(Mi ) |
at these |
points and form the integral sum |
|
|
|
|
|
|
n |
(P(xi , yi ) |
|
yi ) , (7.5) |
y |
|
|
|
∑ |
xi + Q(xi , yi ) |
yi |
|
|
|
i=1 |
|
|
|
Мi |
where |
xi |
and yi |
are projections of a vector |
∆уi |
yi–1 |
Ai-1 |
|
Ai−1 Ai |
(lying on the line segment |
Ai−1 Ai ) onto |
|
|
|
|
Ai L  B
B
the axes Ox and Оу respectively (Fig. 7.3). |
|
A |
∆xi |
x |
Let |
λ = max( |
|
x |
|
, |
|
y |
|
) |
be the greatest |
О |
xi |
xi–1 |
|
|
|
|
|
1≤i≤n |
|
|
i |
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
xi |
|
|
|
|
yi . |
|
Fig. 7.3 |
|
length of projections |
|
|
|
and |
|
|
Definition. If for |
|
λ → 0 |
there exists a finite limit of the integral sum (7.5) |
which depends neither on the way of splitting of the path АВ, nor on a choice of
points Mi in each partial arc, |
then this limit is called a line integral of the |
second type of the functions |
P(x, y) |
and |
Q(x, |
y) |
or a line integral with |
respect to coordinates х and y over a directed curve АВ. It is designated as |
|
|
∫ P(x, y)dx + Q(x, y)dy or ∫ P(x, y)dx + Q(x, y)dy . |
|
|
AB |
|
|
|
L |
|
|
|
|
|
So, by definition |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
n |
|
i i |
i |
i i |
i ) |
|
|
P(x, y)dx + Q(x, y)dy = lim |
∑( |
|
|
|
|
|
|
P(x , y ) |
x |
+ Q(x , y ) |
y . |
|
|
L |
|
λ→0 i=1 |
|
|
|
|
|
|
Remark. A line integral
∫ P(x, y, z)dx + Q(x, y, z)dy + R(x, y, z)dz
L
over a spatial curve L is defined similarly.
155
http://vk.com/studentu_tk, http://studentu.tk/
Theorem If a curve АВ is smooth, and functions P(x, y) and Q(x, y) are continuous over the curve АВ, the line integral of the second type
∫ P(x, y)dx + Q(x, y)dy exists.
AB
Functions P(x, y) and Q(x, y) can have miscellaneous mechanical meanings. In particular, if a material point moves along the curve L under action
of a variable force F = {P (x, y), Q(x, y)} , where |
P(x, y) |
and Q(x, y) are |
coordinates of the vector of force then the line integral |
∫ P(x, |
y)dx + Q(x, y)dy |
|
AB |
|
expresses the work done by the force F at moving a material point along the curve L from the point A to the point B.
7.4. Evaluation and Properties of Line Integrals
of the Second Type
1. Let a curve L be given by the equations x = x(t) , y = y(t), α ≤ t ≤ β , then dx = x′(t) dt , dy = y′(t) dt and a line integral is reduced to the definite integral
∫ |
β |
(P(x(t), y(t))x′(t) + Q(x(t), y(t)) y′(x)) dt. |
|
P(x, y)dx + Q(x, y)dy = ∫ |
(7.6) |
AB |
α |
|
|
2. Let a curve L be given by the equation y = f (x) , a ≤ x ≤ b . In this case dy = f ′(x) dx and a line integral is evaluated by the formula
b |
|
∫ P(x, y)dx + Q(x, y)dy = ∫(P(x, f (x)) + Q(x, f (x)) f ′(x))dx. |
(7.7) |
a |
|
Similarly, if the curve АВ is given by the equation x = g( y) , c ≤ y ≤ d, the line integral is evaluated by the formula
|
d |
(P(g( y), y))g ′( y) + Q(g( y), y)) dy . |
∫ P(x, y)dx + Q(x, y)dy = ∫ |
AB |
c |
|
|
|
3. Let functions P(x, y, z) , Q(x, |
y, z) and R(x, y, |
z) be determined and |
continuous over a space curve АВ which is given by the equations |
x = x(t) , |
y = y(t) , z = z(t) , α ≤ t ≤ β , |
where |
the functions x(t) , |
y(t) , z(t) |
together |
with derivatives x′(t) , y′(t) , |
z′(t) are continuous on an interval [α, |
β] . Then |
there exists a line integral |
|
|
|
|
156
http://vk.com/studentu_tk, http://studentu.tk/
∫ P(x, y, z)dx + Q(x, y, z)dy + R(x, y, z)dz,
|
|
AB |
|
defined by the formula |
|
|
∫ P(x, y, z)dx + Q(x, y, z)dy + R(x, y, z)dz = |
|
β |
AB |
|
(P(x(t), y(t), z(t))x′(t) + Q(x(t), y(t), z(t)) y′(x) + R(x(t), y(t), z(t))z′(t)) dt. |
|
= ∫ |
α
4. Let a contour of integration be a line segment lying in the plane Oxy and parallel to the axis Oy (Fig. 7.4, а). Then its equation is x = x0 , so dx = 0 . If to
take |
y1 ≤ y ≤ y2 , the line integral looks as follows |
|
|
|
|
|
|
|
|
|
|
|
∫ P(x, y)dx + Q(x, |
y2 |
|
|
|
|
|
|
y)dy = ∫ |
Q(x0 , y)dy. |
|
|
(7.8) |
|
|
L |
y1 |
|
|
|
|
Similarly, if the line of integration is parallel to the axis |
Ox (Fig. 7.4, b), |
then |
y = y0 , dy = 0 , therefore |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
∫ P(x, y)dx + Q(x, y)dy = ∫ |
P(x, y0 ) dx. |
|
|
|
|
L |
x1 |
|
|
|
|
а b
Fig. 7.4
If the contour of integration consists of some parts which have different equations, the integral is equal to the sum of the integrals evaluated for each part.
It follows from formulas (7.6) — (7.7) that a line integral of the second type has properties similar to properties of a definite integral. In particular, we must note that if a direction of integration is reversed the line integral of the second type changes the sign by opposite:
∫ P(x, y)dx + Q(x, y)dy = − ∫ P(x, y)dx + Q(x, y)dy,
AB BA
157
http://vk.com/studentu_tk, http://studentu.tk/

while the line integral of the first type does not depend on a direction of integration. Actually, with change of a direction of integration projections of a
vector Ai−1 Ai onto the axes Ox and Оу change their signs (Fig. 7.3).
If a curve of integration L is closed (Fig. 7.5) we get the line integral over the closed contour (or a contour integral) often designated as:
∫ Pdx + Qdy.
L
The value of the contour integral depends solely on the orientation of the contour, that is, on the direction of integration. The closed contour L is termed positively oriented if the contour is traced counter-clockwise, and if otherwise then negatively oriented.
|
|
|
|
|
|
7.5. Green’s Formula |
|
|
|
|
|
В y2(x) |
|
Green’s formula provides |
connection bet- |
|
y |
ween a line integral over a closed contour L and |
|
|
L |
|
|
a double integral over the domain D bounded by |
|
А |
|
|
|
|
this contour. |
|
|
|
|
|
|
|
D |
|
С |
Let functions P(x, |
y) and Q(x, y) |
|
|
|
|
|
|
|
|
|
|
|
|
|
Theorem |
|
|
|
y1(x) |
K |
|
|
|
be continuous together with their |
|
О a |
partial derivatives of the first order in a closed |
|
|
|
b x |
|
|
|
domain D, then the line integral over the closed |
|
|
Fig. 7.5 |
contour L, bounded by the domain D (Fig. 7.5), |
|
|
is connected with the double integral over the |
|
|
|
|
|
|
|
|
|
|
|
|
domain D by Green’s formula |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂P |
− |
∂Q |
|
|
(7.9) |
|
|
|
|
|
∫ Pdx + Qdy = ∫∫ |
∂y |
dxdy |
|
|
|
|
|
|
L |
|
D ∂x |
|
|
|
|
where direction of integration along the contour L is positive (counterclockwise).
Proof. Let a domain D, called regular (Fig. 7.5), be bounded by a positively oriented contour L having at most two common points with every straight line parallel to the axis Ox or Oy. We can prove, that
|
|
– ∫ Pdx = ∫∫ |
∂P |
dxdy. |
|
|
|
|
|
∂y |
|
|
|
We have |
|
L |
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫∫ |
|
b |
y |
(x) |
|
|
|
b |
y |
|
(x) |
∂Pdxdy = ∫ dx |
|
2∫ |
∂P dy =∫ P(x, y) |
|
2 |
dx = |
D |
∂y |
a |
y1 (x) |
∂y |
|
|
a |
y1 (x) |
|
|
|
|
|
|
|
158
http://vk.com/studentu_tk, http://studentu.tk/

b |
|
|
b |
= ∫ (P(x, y2 (x)) − P(x, y1 (x)))dx = ∫ P(x, y2 (x))dx − |
a |
|
|
a |
b |
|
|
|
−∫ P(x, y1 (x))dx = ∫ P(x, y)dx − ∫ P(x, y)dx = |
a |
ABC |
|
AKC |
= − ∫ P(x, y)dx − ∫ P(x, y)dx = − ∫ |
P(x, y)dx = −∫ P(x, y)dx. |
CBA |
AKC |
AKCBA |
L |
By analogy, it is possible to prove that |
∫ Qdy = ∫∫ ∂∂Qx dxdy. |
|
|
L |
D |
Taking into account linearity of a line integral of the second type, the statement of the theorem turns to be true.
Remark. Green’s formula is valid for any domain which can be split into a finite number of regular domains.
7.6. Independence of a Line Integral of a Path of Integration
If a value of a line integral of the second type remains constant over all possible curves connecting initial and terminal points of integration, then the line integral is said to be independent of the form of a path of integration.
Let us remind the concept of simple and multiple connected domains.
A domain is said to be simple connected if it is bounded by one closed without points of self-intersection continuous piecewise smooth curve. So, shown on Fig. 7.6: a) is a simple connected domain; b) is a doubly connected domain; c) is a triply connected domain.
|
а |
b |
c |
|
Fig. 7.6 |
|
|
Let the functions P(x, |
y) and Q(x, |
y) be continuous together |
Theorem |
with their partial derivatives of the first order in a simply connected domain D. Then, for the line integral ∫ P(x, y)dx + Q(x, y)dy, to be
L
independent of the path of integration lying within the domain D it is necessary and sufficient that for all the points of the domain D the condition
should hold.
159
http://vk.com/studentu_tk, http://studentu.tk/
In conditions of this theorem the following statements are valid:
а) the expression under the integral sign is the total differential of a function u(x, y) , i.e.
P(x, y)dx + Q(x, y)dy = du(x, y) ;
b) ∫ P(x, y)dx + Q(x, y)dy = u(xB , yB ) − u(xA , yA ),
L
where A(xA , yA ) and B(xB , yB ) are initial and terminal points of the path of
integration;
c) the line integral taken round any closed contour L lying entirely within the domain D is equal to zero:
∫ P(x, y)dx + Q(x, y)dy = 0.
L
It is possible to prove that the statement of the theorem and the statements а) — c) are equivalent, i.e. each of them implies three others.
Let the condition ∂∂Py = ∂∂Qx be valid, then, after using Green’s formula (7.9), we receive
|
∂Q |
− |
∂P |
∫ P(x, y)dx + Q(x, y)dy = ∫∫ |
∂x |
dxdy = 0. |
L |
D |
|
∂y |
So, it follows from the theorem that the condition c) is fulfilled.
Let us assume, that the condition b) is fulfilled, i.e. the expression under the integral sign is the total differential of the function u(x, y) :
P(x, y)dx + Q(x, y) = du(x, y),
on the other hand, by definition of differential
|
|
|
|
|
du = |
∂u dx + ∂u dy. |
|
|
|
|
|
|
|
|
|
|
|
∂x |
|
∂y |
|
|
|
|
|
|
|
Thus, |
∂u = P(x, y), |
∂u |
= Q(x, y). |
|
Then |
by the |
theorem |
of mixed |
|
|
|
∂x |
∂y |
|
|
|
|
|
|
|
|
|
|
|
|
derivatives |
the equalities |
∂2u |
|
= |
∂P |
, |
∂ 2u |
= |
∂Q |
are |
fulfilled, |
therefore |
|
∂x∂y |
∂y |
∂y∂x |
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
∂P |
= ∂Q . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂y |
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
If the line integral ∫ P(x, |
y)dx + Q(x, |
y)dy is path-independent, its value is |
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
defined by initial and terminal points of integration. |
|
|
|
|
160 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
http://vk.com/studentu_tk, http://studentu.tk/











 А
А