Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный авиационный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Higher_Mathematics_Part_3

.pdf

Скачиваний:

304

Добавлен:

19.02.2016

Размер:

9.11 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 248 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 > Следующая >>>

Examples of orthogonal functions:

1) system of functions

1, sin x, cos x, sin 2x, cos 2x, sin 3x, cos 3x, …, sin nx, cos nx, …

is orthogonal on a segment [−π; π] ; 2) systems of functions

1, cos x, cos 2x, cos 3x, …, cos nx, …

and

sin x, sin 2x, sin 3x, …, sin nx, …

are orthogonal on a segment [0; π] ; 3) system of functions

1, sin πlx , cos πlx , sin 2πl x , cos 2πl x , …, sin nπl x , cos nπl x , …

is orthogonal on a segment [−l; l] ; 4) systems of functions

1, cos πlx , cos 2πlx , …, cos nπlx , …

and

sin πlx , sin 2πl x , …, sin nπl x , …

are orthogonal on a segment [0; l] .

Let’s calculate the coefficients of trigonometric series (3.2). We integrate both sides of equality (3.2) from −π to π to calculate a0 .

∫

-π

Therefore,

Then

π	a0	∞	π	π
f (x)dx = ∫		dx + ∑ an ∫ cos nxdx + bn ∫ sin nxdx .
f (x)dx = ∫	2	dx + ∑ an ∫ cos nxdx + bn ∫ sin nxdx .
-π	2	n=1	-π	-π
π			π
∫	cos nxdx = 0;		∫ sin nxdx = 0.
− π			− π

∫f (x)dx = π a0 .

− π

		1	π
a0	=		∫ f (x)dx .	(3.8)

		π − π

To compute ak we multiply both sides of equality (3.2) by cos kx and integrate both sides from −π to π. To compute bk we multiply both sides of equality (3.2) by sin kx and integrate both sides from −π to π.

http://vk.com/studentu_tk, http://studentu.tk/

We receive

		1	π
ak	=		∫	f (x)cos kxdx,	(3.9)
		π
			− π
		1	π
bk	=		∫	f (x)sin kxdx.	(3.10)

		π − π
Definition. The coefficients	a0 ,		an , bn obtained by formulas (3.8), (3.9) and

(3.10) are called Fourier coefficients. Trigonometric series with these coefficients is called Fourier series.

For integrable function f (x)

on a segment [−π; π] we write:

∞

f (x) ~

+ ∑(an cos nx + bn sin nx).

(3.11)

n=1

The sign

(~) denotes that Fourier series corresponds the function f (x)

integrable on a segment [−π; π] .

Let’s consider sufficient conditions for representation of a function

f (x) by

Fourier series.

Theorem

(Dirichlet’s). Suppose Dirichlet’s conditions are fulfilled for

1) f (x)

2π-periodic function f (x) on segment [−π; π] :

is a piecewise continuous (continuous or has finite number of

finite discontinuities),

2) f (x)

is a piecewise monotone.

Then Fourier series of a function f (x) is convergent everywhere and its

sum S(x) has the following properties:

1) S(x) = f (x) at points of continuity f (x) , that is

∞

f (x) =

+ ∑ (an cos nx + bn sin nx) ;

2) if x0

n=1

f (x) ,

is a point of discontinuity of the first type of a function

then

f (x0 − 0) + f (x0

+ 0)

S(x0 ) =

3) at the end points x = −π,

x = π of a segment [−π; π]

S(−π) = S(π) =

f (−π + 0) + f (π − 0)

http://vk.com/studentu_tk, http://studentu.tk/

Remarks.

1. For any integrable 2π-periodic function ϕ(x) the following equality is true

			π					a+ 2π
			∫	ϕ(x)dx =				∫		ϕ(x)dx .
			− π					a
Therefore we can calculate Fourier coefficients by the formulas
a =	1	a+ 2π	f	(x)dx, a				=	1		a+ 2π f (x) cos nxdx ,
a =	π	a+ 2π	f	(x)dx, a				=	π		a+ 2π f (x) cos nxdx ,
0	π	∫					n		π		∫
0							n
		a									a
		b		=	1	a+ 2π	f (x)sin nxdx,
		b		=	π	a+ 2π	f (x)sin nxdx,
			n		π	∫
			n
						a

where a is an arbitrary real number.

2. If Sn (x) is the n-th partial sum of Fourier series of a function f (x) then

f (x) ≈ Sn (x) = a0 + ∑n (ak cos kx + bk sin kx). 2 k =1

3. Whereas an cos nx + bn sin nx = An sin(nx + ϕn ) then Fourier series of a

function

f (x) is

∞

f (x) = A0 + ∑(An sin(nx + ϕn )).

n=1

Numbers

ωn = 0, 1, 2, ...

form

a discrete

spectrum of a function

f (x) ;

numbers

, A

= a2

+ b2

( n = 1,

3, ... ) form amplitude spectrum,

numbers ϕn = arctg

( n = 1,

2, 3, .... ) form phase spectrum of a function

f (x).

sin nπ = 0,

cos nπ =

(

)

n ,

n = 0, 1, 2, ... .

−1

3.2. Fourier Series for Odd and Even Functions

If f (x) is either odd or even function we can simplify the calculation of Fourier coefficients. Fourier series for these functions are given in Table 3.1.

http://vk.com/studentu_tk, http://studentu.tk/

											Table 3.1

Property of a function f (x)	f (x)			is an even function				f (x)	is an odd function

		a0			∞				∞
Fourier series		a0		+ ∑an cos nx					∑bn sin nx
Fourier series	2			+ ∑an cos nx					∑bn sin nx
	2				n=1				n=1

	b = 0, a =					2	π f (x)dx ,	a = 0, a = 0,
	b = 0, a =						π f (x)dx ,	a = 0, a = 0,
	n				0	π ∫			0		n
	n				0				0		n
Fourier coefficients					π	0			2 π
Fourier coefficients					π				2 π
	an =		2		∫ f (x)cos nxdx			bn =		∫0	f (x)sin nxdx
			2					bn =	π		f (x)sin nxdx
			π						π
					0

3.3. Fourier Series for 2l-periodic Functions

It is possible to expand in Fourier series 2l-periodic functions (2l ≠ 2π). Suppose a function f (x) is defined on a segment [−l; l] and has a period

2l ( l is an arbitrary positive real number). Suppose this function obeys all

conditions of Dirichlet’s theorem. Therefore Fourier series for

f (x) looks like

∞

πnx

f (x) =

∑

cos

+ bn sin

(3.12)

n=1

where Fourier coefficients are obtained by using the following formulas

1 l

πnx

a =

∫

f (x)dx,

a =

l ∫

f (x)cos

dx,

−l

(3.13)

1 l

πnx

l ∫

f (x) sin

dx.

−l

We can obtain formulas (3.12), (3.13) for function

ϕ(t) using

formulas

(3.2), (3.8) — (3.10) and the connection between ϕ(t) and

f (x) .

x =

, t [−π;

, ϕ(t) = f (x) =

π].

Remark. All theorems for Fourier series of 2π-periodic functions take place for Fourier series of 2l-periodic functions.

http://vk.com/studentu_tk, http://studentu.tk/

Fourier series and Fourier coefficients for even and odd functions defined on segment [−l; l] are given in Table 3.2.

Table 3.2

Property of a

f (x)

is an even function

f (x)

is an odd function

function f (x)

∞

πnx

∞

Fourier series

+ ∑an cos

∑bn sin πnx

n 1

b = 0, a =

f (x)dx,

a = 0, a = 0,

Fourier

l ∫0

πnx

coefficients

∫

f (x)sin

f (x) cos πnx dx

∫

3.4. Fourier Series for Functions Defined on a Segment [0; l]

or on an Arbitrary Segment [a; b]

Suppose a function

f (x) is defined on a segment

[0; l] . Let’s extend this

function on an interval

(−l; 0)

in arbitrary way and extend this function perio-

dically with period

2l . We can expand this function in Fourier series using

formulas (3.12), (3.13).

The most popular cases are:

1. We extend a function

f (x) from a segment [0; l]

on interval

(−l; 0) in

even way that is

f (− x) = f (x) for

x (−l; 0) (Fig. 3.1, а). Then we can consi-

der a function f (x)

as an even function on interval (−l; l) . Therefore Fourier

series for this function contains only cosines.

2. We extend a function

f (x)

from a segment [0; l]

on interval (−l; 0) in

odd way that is

f (− x) = − f (x)

for

x (−l; 0) (Fig.

3.1, b). Then

we can

consider a function	f (x)	as an odd function on interval (−l; l) . Therefore Fourier
series for this function contains only sines.
	y у = f (x)			y у = f (x)
– l	O	l	x	– l O	l	x
	a				b
			Fig. 3.1
						75

http://vk.com/studentu_tk, http://studentu.tk/

Suppose a piecewise monotone function f (x) is given on a segment [a; b],

where a < b.

Let’s consider a periodic extension of this function for all real axis

with period T = b − a . That is we get a function f1 (x)

so that f1 (x) = f (x) for

x (a; b) and f1 (x + T ) = f1

(x) . We denote 2l = T = b − a. Therefore l =

b − a

The following equality is fulfilled for the function f1(x) :

a+ 2l

∫ f1 (x)dx = ∫ f1 (x)dx = ∫ f (x)dx .

Then

−l

∞

πnx

f1 (x) ~

+ ∑

an cos

+ bn sin

n=1

where Fourier coefficients are obtained by formulas

1 b

πnx

a =

∫

(x)dx,

l ∫

f (x) cos

dx,

(3.14)

1 b

πnx

− a

∫

f (x) sin

( l =

f1 (x) = f (x)

for x (a; b)

therefore the sum of Fourier series is equal to f (x)

at all points of continuity of segment [a; b] .

3.5. Complex Form of Fourier Series

Sometimes we use Fourier series in a complex form. We apply Euler’s formulas

cos nx =	einx + e−inx	, sin nx =	einx − e−inx	.
	2		2i

Then we can write Fourier series for 2π-periodic function f (x) as

		n=∞
		f (x) = ∑ cn einx .	(3.15)
		n=−∞
Coefficients of this series are

	π
	cn = ∫ f (x)e−inx dx ( n = 0, ± 1, ± 2, ... ).		(3.16)
	−π

http://vk.com/studentu_tk, http://studentu.tk/

Definition. An equality (3.15) is called a complex form of Fourier series of a function f (x) and numbers cn (3.16) are called the complex Fourier coefficients.

Micromodule 3

EXAMPLES OF PROBLEMS SOLUTION

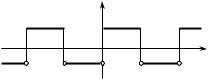
Example 1. Expand 2π-periodic function

−1, if		x [0; π],
f (x) =	2, if	x (−π;0),

( f (x + 2π) = f (x) ( Fig. 3.2)) into Fourier series.

	у
	2
–π	О	π	х
	–1

Fig. 3.2

Solution. The given function is satisfied to all conditions of Dirichlet’s theorem. We can expand it in Fourier series. Let’s calculate coefficients a0 , an ,

bn using formulas (3.8) — (3.10). We get

∫

f (x)dx =

∫

(−1)dx +

∫

− x

+ 2x

= 1;

π −π

2dx =

π − π

−π

∫

f (x) cos nxdx =

∫

− cos nxdx +

∫

2 cos nxdx

− π

π −π

sin nx

2 sin nx

−

= 0;

−π

1 cosnx

2cosnx

bn =

∫

f (x)sin nxdx =

∫

−sin nxdx +

∫

−

2sin nxdx

−π

π −π

−π

(cos 0 − cos(−πn) −

2cos πn + 2 cos 0) =

3(1− (−1)n )

πn

If we substitute values of coefficients a0 , an ,

in formula (3.2) we get

∞ 3(1− (−1)n )

f (x) =

+ ∑

sin nx.

πn

n=1

http://vk.com/studentu_tk, http://studentu.tk/

	0,		if	n = 2k,
	6
=	6	,	if	n = 2k − 1,

	π(2k − 1)
	π(2k − 1)

then expansion in Fourier series is

	1		6	∞	sin(2k −1)x
f (x) =		+		∑		.
	2		π k =1		2k −1

This equality is fulfilled for all points of continuity of the given function, that is for x ≠ πn . At points of discontinuity x = πn the sum of the series equals

arithmetic mean of one-sided limits at these points. Therefore S(πn) = −1+ 2 = 1 . 2 2

Remark. If f (x) = g(x) + C, is an odd function, C is a constant, then Fourier series for f (x) looks like

			a0	∞
		f (x) =	a0	+ ∑bn sin nx.
		f (x) =		+ ∑bn sin nx.
		2		n=1
Example 2. Expand 2π-periodic function
0, if	x (−π; 0),	( f (x + 2π) = f (x) (Fig. 3.3)) in Fourier series.
f (x) =	x [0; π],	( f (x + 2π) = f (x) (Fig. 3.3)) in Fourier series.
x, if	x [0; π],

Solution. The given function is piecewise monotone. Therefore it may be expanded in Fourier series. Let’s find Fourier coefficients for function f (x) :

1 x2

a0 =

∫

0 dx

∫

;

xdx

π 2

π −π

∫

cos nxdx +

∫

x cos nxdx =

x cos nxdx

−π

u = x,

dv = cos nxdx

sin nx

π sin nx

sin nx

−

∫

du = dx,

v =

(−1)n − 1

cos nx

;

πn2

∫

sin nxdx +

∫

x sin nxdx =

x sin nxdx

π −π

http://vk.com/studentu_tk, http://studentu.tk/

u = x, dv = sin nxdx

cos nx

π cos nx

cos nx

− x

∫ n

du = dx, v = −

(−1)n+1 π

(−1)n+1

sin nx

πn

Therefore Fourier series for the given function looks like

∞

(−1)n −1

(−1)n+1

f (x)

+ ∑

cos nx +

sin nx

πn

n=1

cos x

f (x)

cos3x

cos5x

sin x

sin 2x

sin 3x

−

+ …

−

− … .

At all points of continuity of

f (x)

the sum of the series equals the value of

function

f (x) . At points of discontinuity

x = −π + 2πk, k Z

the sum of the

series equals

π .

x = 0

f (x), therefore

is a point of continuity of function

f (0) =

−

…

But f (0) = 0,

then

2 1

0 =

−

+ …

Therefore

π 1

+ …+

+ …=

π2

Conclusion. We can find the sum of numerical series using Fourier series. Example 3. Expand 2π -periodic function

f (x) = | x |, ( f (x + 2π) = f (x) (Fig. 3.4)) into Fourier series.

Solution. The given function is satisfied to all conditions of Dirichlet’s theorem. It is even function. Then Fourier series for this function looks like

	a0	∞
f (x) =		+ ∑ an cos nx .

2		n=1

http://vk.com/studentu_tk, http://studentu.tk/

Let’s find Fourier coefficients a0 and an (Table 3.1):

2 π

xdx =

2 x2

= π;

π ∫

π 2

sin nx

π sin nx

∫

x cos nxdx =

−

∫

2 cos nx

((−1)n − 1).

πn2

–2π –π О

π 2π х

–2π –π О

2π х

Fig. 3.3 Fig. 3.4

That is Fourier series for the given function is

f (x) = π +

∞

(−1)

− 1

π −

∞

cos(2k −1)x

∑

cos nx =

∑

π n=1

π k =1

(2k −1)2

4 cos x

cos 3x

cos 5x

−

+ … .

(3.17)

The given function f (x)

is continuous everywhere. Therefore formula (3.17) is

true for all x R .

Example 4. Expand function

f (x) = x2 ,

x [0; π]

in sine series.

Solution. Let’s extend

f (x)

in odd way on

[−π; 0) , and then extend it

periodically with period

2π on all numerical axis (Fig. 3.5). Function

f (x) is

odd on a segment [−π; π] . Therefore

a0 = an

= 0 . Let’s find a coefficient bn

2 π using formula bn = π ∫0

We get

b = 2 π x2

n π ∫0

f (x)sin nxdx .

	2		2	− cos nx
sin nxdx =		x		n
sin nxdx =		x
	π

π	2	π
+	2	∫0	x cos nxdx	=
+	n		x cos nxdx	=
0	n

http://vk.com/studentu_tk, http://studentu.tk/

<<< < Предыдущая 1 2 3 4 5 6 78 / 248 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
19.02.20169 Mб95Higher_Mathematics_Part_1.pdf
#
19.02.20166.63 Mб1052Higher_Mathematics_Part_1.pdf
#
19.02.20169.73 Mб45Higher_Mathematics_Part_2.pdf
#
19.02.20167.48 Mб408Higher_Mathematics_Part_2.pdf
#
19.02.20167.31 Mб123Higher_Mathematics_Part_2.pdf
#
19.02.20169.11 Mб304Higher_Mathematics_Part_3.pdf
#
19.02.2016694.82 Кб11HiraganaKatakanaWorkSheet (1).pdf
#
11.09.2019192.23 Кб1hjuj;f.docx
#
27.11.2019386.05 Кб9How Airplanes Work.doc
#
20.11.201958.78 Кб8I exercise 5.docx
#
19.02.201615.51 Mб28IFPS.pdf