Для граничных сечений III участка получим следующие значения нормальных сил и напряжений:

при z₃ = 0,8 м:

при z₃ = 1,2 м,

0. Построение эпюр N_z и s_z

По полученным значениям N_z и s_z для граничных сечений каждого участка строим их эпюры (рис. 4.4д). После построения эпюр следует проверить соответствие эпюры N_z действующим внешним силам (скачок в сечении В, должен быть равен Р = 200 · 10² Н), скачки в эпюре s_z должны совпадать с точкой приложения внешней силы Р и изменения размеров поперечного сечения по участкам колонны.

4.4.4 Вычисление перемещения верхнего конца колонны от действия всех сил

Полное перемещение согласно закону Гука может быть вычислено по формуле:

Для трех участков колонны укорочения ее длины Δ l может быть записано в виде:

Поскольку численные значения определенного интеграла равны площади, очерченной под интегральный функцией, то для вычисления этих интегралов, т.е. перемещений Δ l_i, достаточно вычислить площадь эпюры N_z на каждом из участков и разделить на Е_i A_i.

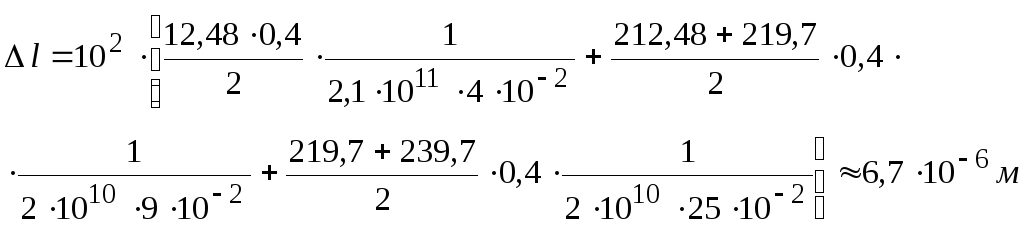
Следовательно, с другой стороны, это перемещение можно вычислить иначе, воспользоваться принципом независимости действия сил, а именно:

.

При этом следует помнить, что перемещение от действия внешних сосредоточенных сил вычисляется по формуле:

а от действия собственного веса (при Е_i A_i=const)

как

где .

С учетом указанного, вычисление перемещения для каждого участка будет записано в виде:

Тогда полное укорочение (перемещение) верхнего конца колонны (при l₁=l₂=l₃) будет:

Подставляя в указанные выражения следующие значения сомножителей и слагаемых, получим

Таким образом, результаты вычисления совпадают.

5. Расчет гибких нитей

Совершенно гибкой называется нить, которая способна сопротивляться только растяжению. Из шести компонентов внутренних сил в поперечных сечениях такой нити только осевая растягивающая сила не равна нулю. В инженерной практике широко распространены системы, с известным приближением могут рассматриваться как гибкие нити. Таковы воздушные линии электрических проводов, провода телефонных сетей, контактные провода электрифицированных железных дорог и трамваем, цепи висящих мостов, тросы канатных дорог и кабель кранов и т.п.

Точки подвеса нити могут находиться на одном или на разных уровнях (рис. 5.1).

Рисунок 5.1.

При расчете на прочность длинных гибких нитей, кроме других нагрузок, существенное значение имеет их собственный вес. Пусть весомая гибкая нить постоянного поперечного сечения подвешена в двух точках, расположенных на разных уровнях (рис.5.1). Под действием собственного веса нить провисает по некоторой кривой.

Введем следующие обозначения:

l₁ – расстояние между точками А и В подвеса нити;

l – пролет, равный горизонтальной проекций расстояние l₁;

h – разность уровней точек подвеса нити;

f – удаление нити от прямой АВ, соединяющей точки подвеса нити,

измеренное посредине пролета;

L – длина неподвешенной нити;

q – интенсивность нагрузки на единицу длины нити.

В случае одинаковых уровня точек подвеса величина f является удлинением низшей точки нити от горизонтальной линии АВ и называется стрелой провисания. Нагрузка q может быть не только собственным весом, но и включать в себе другие нагрузки, например, вес льда при обледении проводов, давление ветра. Эти нагрузки предполагаются также равномерно распределенными пол длине нити.

В случае, когда нагрузка состоит из собственного веса нити, ее интенсивность

(5.1)

где q_п – вес единицы длины провода;

 - вес единицы объемного материала;

А – площадь поперечного сечения нити.

При обледении проводов

(5.2)

где q_л – вес льда на единице длины провода.

Толщину корки льда принимают величиной 0,5-25 см в зависимости от климатического района.

Перечисленные нагрузки действуют в вертикальной плоскости, давление же ветра на провод в горизонтальной плоскости. Интенсивность его q_в определяют, умножая давление ветра р на площадь диаметрального сечения единицы длины провода:

q_в = р d

или

q_в = k  q_ск d

где k = 1,2 аэродинамический коэффициент;

 = 0,85 коэффициент неравномерность ветра;

q_ск – скоростной напор;

d – диаметр провода с учетом его увеличения за счет обледения.

Выражаю q_ск через скорость ветра V, получим:

q_в = 636  10^-3 V² d Н/м (5.4)

Здесь V измеряет в м/с, а d – в м.

Суммарная интенсивность нагрузки на провод найдем в результате геометрического сложения суммарных вертикальной и горизонтальной нагрузок:

(5.5)

При этом, естественно, плоскость действия суммарной нагрузки, совпадающая с плоскостью провисания нити, не будет вертикальной.

На практике провисание нити чаще всего бывает небольшим – таким, при котором длина нити по кривой провисания мало обличается от длины пролета (обычно не более, чем на 10%) ограничимся рассмотрением только таких пологих нитей. В этом случае для упрощения расчетов с достаточной степенью точностью можно считать, что нагрузка, действующая на подвешенную нить, равномерно распределена не по длине нити, а по длине отрезка АВ, соединяющего точки подвеса (рис. 5.2).

Рисунок 5.2

Для удобства вычислений эту нагрузку заменяем статически эквивалентной нагрузкойq, распределенной вдоль пролета l.

Очевидно.

Отсюда

(5.6)

Статическая сторона задачи. Рассмотрим равновесия нити. Так как нить предполагается совершенно гибкой, то растягивающие усилия в каждом поперечном сечении должны быть направлены по касательной к кривой провисания нити. В точках прикрепления эти усилия равны реакция опор. Обозначим последние соответственно через Т_А и Т_В. Выбираем начало координат в левой точке подвеса нити и направим оси координат так, как показано на рисунке 5.2.

Заменяя реакции опор их горизонтальными и вертикальными составляющими, запишем уравнения равновесия нити:

(5.7)

Из уравнений (5.7) следует, что

(5.8)

(5.9)

(5.10)

Так как их трех уравнений равновесия нельзя определить четыре неизвестных (Н_А, V_А, Н_В, V_В), то задача является один раз статически неопределимой.

Рассмотрим равновесие части нити, отсеченной любым сечением (рис. 5.3):

 х = 0; – Н + Т (х) = 0;

 у = 0; – V_A + q х + T_y (х) = 0;

Рисунок 5.3

Отсюда с учетом формулы (5.9) получим:

T_у (х) = Н; (5.11)

(5.12)

Как видно из выражения (5.11) горизонтальная составляющая растягивающегося усилия в любом поперечном сечении нити постоянна и равна величине Н. Усилие Н называется горизонтальным натяжением нити.

Таким образом, растягивающее усилие в произвольном сечении нити

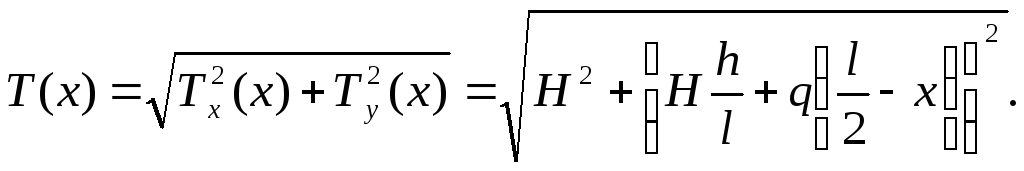(5.13)

Как видно, наибольшее растягивающее усилие Т_тах действует в высшей точке подвеса нити (при х = 0);

Для пологих нитей различие между наибольшим растягивающим усилием, действующим у более высокой точки подвеса, и натяжением Н невелико. Поэтому с достаточной для практики точностью можно считать, что растягивающее усилие в нити постоянно и равно величине натяжения Н. по этой величине обычно и ведут расчет нити на прочность.

Выясним форму кривой провисания нити. С этой целью запишем уравнение для изгибающего момента в каком-либо сечении (рис. 5.3). Поскольку нить совершенно гибкая, то во всех ее сечениях изгибающий момент равен нулю:

(5.14)

С учетом формулы (5.9) получим:

(5.15)

откуда

(5.16)

т.е. кривая провисания нити выражения квадратной параболой.

Определим возможные положения низшей точки кривой провисания нити. Координаты этой точки обозначим через х = а, у = (рис. 5.4 а).

а) б)

в)

Рисунок 5.4

В ней у имеет экстремальное значение. Для определения его возьмем производную от выражения (5.16):

(5.17)

и приравниваем ее нулю:

(5.18)

Отсюда найдем значение абсциссы, определяющее положение низшей точки:

(5.19)

Низшая точка кривой провисания нити всегда находится ближе к более низкой точке подвеса.

Подставляя выражения (5.19) в формулу (5.16), найдем экстремальное значение ординаты, т.е. величину наибольшего провисания нити:

(5.20)

Будем различать три характерных случая расположения низшей точки кривой провисания нити:

1. Низшая точка кривой провисания находится в пределах пролета, т.е. а  l (рис. 5.4 а). Согласно выражению (5.19) это будет иметь место, когда

(5.21)

2. Низшая точка кривой провисания лежат вне пролета, т.е. а  l (рис. 5.4 б). Это будет при условии

(5.22)

3. Низшая точка кривой совпадает с более низкой точкой подвеса, т.е. а = l (рис. 5.4 в). Необходимое условие для этого случая

(5.23)

Во всех трех случаях координат а и низшей точки определяется по формулам (5.19) и (5.20).

Установим зависимость между натяжением Н и величиной f. Посредине пролета а(рис. 5.1). Подставляя эти значения координат в формулу (5.16), получим:

(5.24)

или

(5.25)

Выразим натяжение нити Н через наибольшее провисание . Из формулы (5.20), решая квадратное уравнение относительно натяжениеН, получим:

(5.26)

Если низшая точка кривой провисания лежит в пределах пролета, то перед корнем следует брат знак минус, если вне пролета – знак плюс, так как в первом случае натяжение Н меньше, чем во втором, что видно из сравнения (5.21) и (5.22).

Геометрическая сторона задачи. Установим связь между длиной подвешенной нити, пролетом и величиной f, характеризующей провисание нити. Длина элемента кривой, как известно,

Если нить пологая, то величина мала по сравнению с единицей. Раскладывая выражениев ряд по формуле бинома Ньютона и ограничиваясь первыми двумя членами разложения, получим:

(5.27)

Подставляя сюда из выражения (5.17) и интегрируя по всей длине пролета, будем иметь:

(5.28)

Подставляя на основании формулы (5.25) получим, что

(5.29)

Из геометрических соображений удлинение  S нити длиной L после подвески

(5.30)

Физическая сторона задачи. Установим также физические зависимости, выражающие изменение длины от растягивающего усилия и от изменения температуры. Как указывалось, для пологих нитей растягивающее усилие можно принять равным натяжению Н.

При определении удлинений длину нити заменим длиной l₁, что достаточно точно при малом провисании. Тогда упругое удлинение от растяжения

(5.31)

Температурное удлинение нити определяется по формуле

(5.32)

где t_ – температура в момент подвешивания нити:

t – температура, для которой производится расчет нити.

Суммарное изменение исходной длины нити:

(5.33)

Формулы (5.30) и (5.33) выражают одну и ту же величину удлинение подвешенной нити. Приравняв правые части этих равенств, находим:

(5.34)

Уравнение (5.34) совместно со статическим уравнением (5.24) позволяют определить натяжение нити Н и стрелу провисания f.

Определив из уравнения (5.10) натяжение нити Н, можем по формуле (5.13) вычислить растягивающее усилие в произвольном сечении нити, а значит, и Т_тах зная последнее, проверяем прочность нити:

с учетом формулы (5.25) получим:

(5.35)

При расчете нитей удобно ввести понятие удельной нагрузки , которая представляет собой интенсивность погонной нагрузкиq, отнесенную к площади поперечного сечения нити:

Если действует только собственный вес, удельная нагрузка совпадает с объемным весом материала нити.

С учетом сказанного условия прочности можно записать так:

(5.36)

Заметим, что при расчете электрических проводов сечение нити определяется из электротехнических сооружений, а затем выполняется проверочный расчет.

Приведем расчетные формулы для часто встречающегося случая нити с точками подвеса, расположенными на одном уровне (рис. 5.5) т.е. при cos  = 1.

Рисунок 5.5

В этом случае h = 0, реакции в точках подвеса одинаковы: наибольшее провисанияf будет посредине пролета. Как и ранее, оно связано с натяжением формулами (5.24) и (5.25).

(5.37)

Уравнение совместности деформации (5.34) принимает вид:

(5.38)

Влияние изменение температуры и нагрузки на напряжение и стрелу провисание нити. В процессе эксплуатации нить может подвергаться воздействию различных нагрузок и температур. Выясним, как изменяются напряжения и стрела провисания нити при изменении этих факторов. С этой целью рассмотрим два состояния нити: т и п-е (рис. 5.6).

Рисунок 5.6

Пусть в т-м состоянии температура равна t_m, погонная нагрузка – q_m, а стрела провисания – f_m; при этом натяжение а напряжение в нити

При изменении температуры и нагрузки в п-м состоянии до величин t_m и q_п стрела провисания f_п, натяжение а напряжениеустановим зависимость между напряжениями и стрелами провисания нити для указанных двух состояний.

Задача легко решается, если записать выражение для длины нити L к моменту подвеса через параметры обоих состояний. Если точки подвеса нити находятся в одном уровне, то на основании уравнения (5.38), исходя из параметров т и п-го состояний соответственно получим:

(5.39)

(5.40)

Правые части этих двух выражений, представляющие одну и ту величину – длину нити к моменту подвеса, равны между собой. Следовательно,

Отсюда, обозначая и учитывая, чтонаходим

(5.41)

Эту зависимость иногда называют уравнением состояния нити. Его можно переписать также в виде

(5.42)

Если выразить напряжения через стрелы провисания:

то уравнение (5.42) можно записать так:

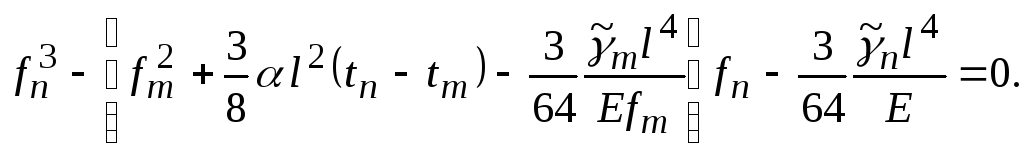(5.43)

Чтобы получить уравнения состояния нитей, подвешенных на разных уровнях (рис. 5.2), в качестве исходной формулы длины l следует взять формулу (5.34). Тогда уравнение состояния (5.41) примет вид:

(5.44)

Выразив, как и выше напряжения через стрелы провисания, получим:

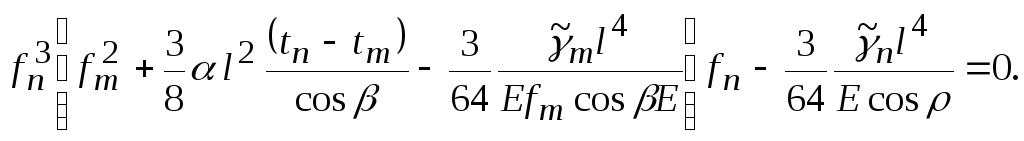(5.45)

Выведенные выше кубические уравнения могут быть решены любым известным методом, в том числе и графическим.

При графическом решении, например, уравнения (5.43)

где а и в – известные числа, запишем последнее уравнение в виде

(5.46)

В прямоугольных координатах строим графики и(рис. 5.7). Очевидно, что абсцисса точки пересечения кубической параболы с прямой дает действительный корень уравнения, а значит и искомую стрелу. Два других корня кубических уравнения мнимые.

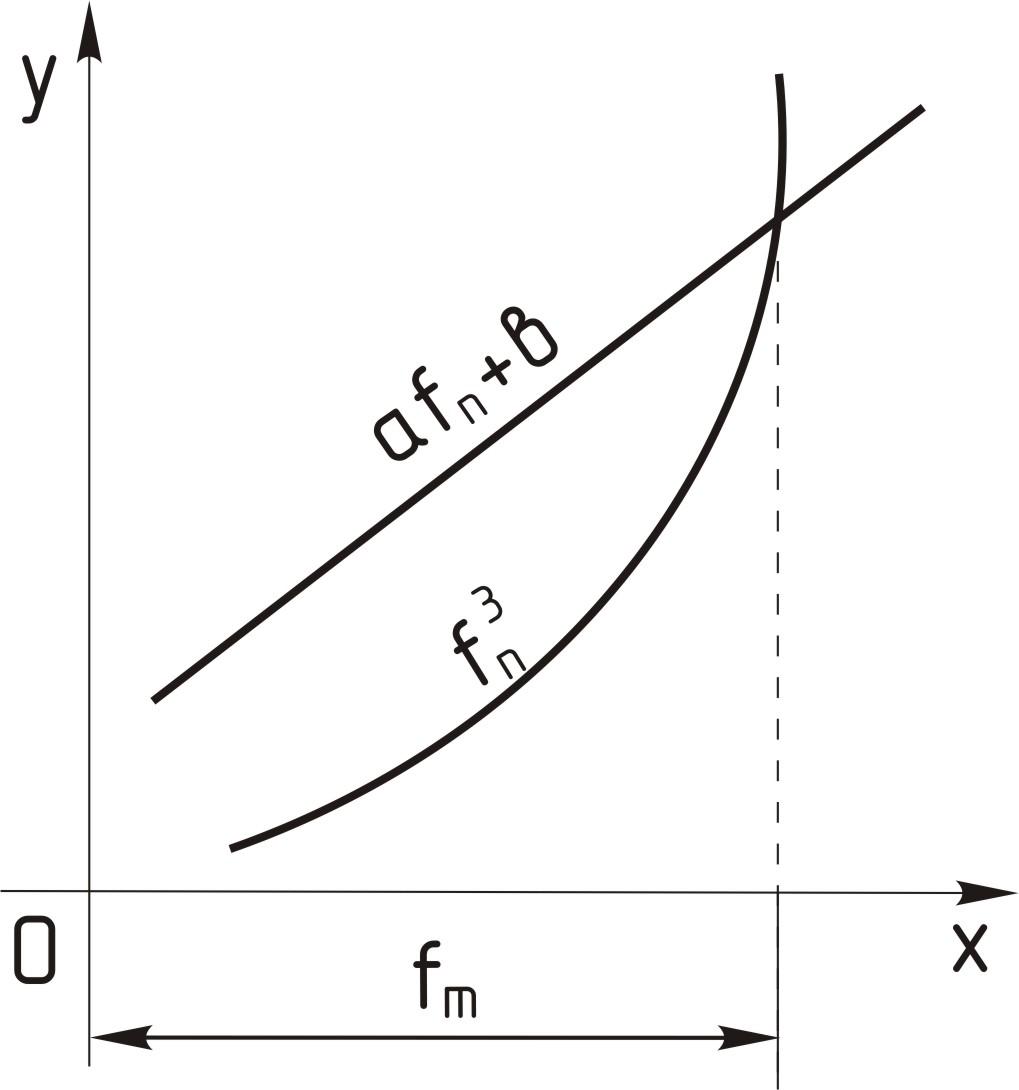
Рисунок 5.7

В случае необходимости уточнить полученное графическим способом решение можно применить способ Ньютона:

где

Понятие о критическом пролете. Расчетом на прочность нужно установить, при каком состоянии нити в ней будет максимальное напряжение. Оно может быть:

а) При наибольшей нагрузке (гололед и умеренный ветер или отсутствие гололеда, но сильный ветер);

б) При самой низкой температуре без гололеда.

Так как наибольшая нагрузка не совпадает во времени с наиболее низкой температурой, то для расчета важно установить, какое из этих состояний будет опасным. Выясним влияние нагрузки и температуры на напряжения в зависимости от длины пролета нити:

Исходим из уравнения состояния (5.41). В случае весьма малых пролетов, положив в этом уравнении l = 0, найдем, что

т.е. при малых пролетах изменение напряжения зависит главным образом от температуры. С уменьшением температуры t_n напряжения _п растут и наибольшие напряжения в нити имеют место при низшей температуре.

Рассмотрим теперь, случай весьма больших пролетов. Разделив уравнение (5.41) на l ² и положив l  , получим:

Следовательно, если пролеты велики, то изменение напряжения в основном зависит от нагрузки на нить. Наибольшие напряжения будут действовать при максимальных нагрузках.

Найдем такую длину пролета, при которой напряжения в нити будут одинаковыми в обоих опасных состояниях, т.е. как при небольшой нагрузке, так и при наиболее низкой температуре. Такой пролет называется критическим (l_кр).

Пусть t_n соответствует температуре гололеда, т.е. t_n = t_гол (обычно t_гол = – 5 С), при этом t_т – соответствует низкой температуре, т.е. t_т = t_тin на нить в этом случае действует собственный вес, так что

При l = l_кр согласно по определению

Внося эти данные в выражения (5.41) находим

(5.47)

Сопоставляя расчетный пролет с критическим, можно установить, при каких условиях в нити действует наибольшее напряжение. Так, если l  l _кр, то наибольшее напряжение будет при низшей температуре. В случае l  l _кр опасное состояние будет при наибольшей нагрузке.