3.2. Принцип Даламбера для системы материальных точек

Рассмотрим теперь механическую систему, состоящую из п материальных точек. Запишем дифференциальные уравнения движения этой системы в некоторой форме:

где равнодействующая активных сил, приложенных к-й точке, аравнодействующая реакций связей, наложенных на эту точку.

Если ввести в рассмотрение силы инерции каждой точки, то эти уравнения примут вид

(3.3)

Система уравнений (14.3) выражает принцип Даламбера для системы материальных точек: если каждой точке движущейся механической системы условно приложить соответствующую силу инерции, то в любой момент движения действующие на эту точку активные силы (внешние и внутренние), сила реакций образует уравновешенную систему сил.

Значение принципа Даламбера состоит в том, что при его применения уравнения движения точки и системы составляются в форме уравнений равновесия. Метод решения динамических задач с помощью принципа Даламбера называют методом кинетостатики.

Однако для решения задач применяют не сам принцип Даламбера, а следствия из него. Для их вывода представим равнодействующую сил, приложенных к к-й точке системы, в виде двух составляющих: равнодействующей внешних вил, приложенных к точке, и равнодействующей внутренних сил, приложенных к точке, т.е.

Тогда система уравнений (14.3), выражающих принцип Даламбера, запишется в виде

(3.4)

Для каждой материальной точки сумма моментов этих уравновешенных сил относительно любого центра 0 также равна нулю, т.е.

(3.5)

Суммируя все уравнения системы (14.4) и системы (3.5), получим

Но по свойству внутренних сил их главный вектор и главный момент равна нулю, и поэтому

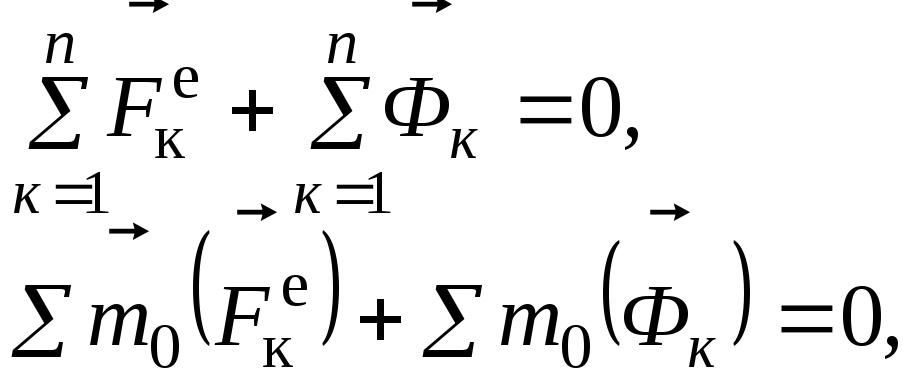(3.6)

т.е. главный вектор и главный момент относительно любого центра приложенных к системе внешних сил и сил инерции всех ее точек равны нулю. Это и есть следствия из принципа Даламбера, которыми пользуются при решении задач.

При практическом использовании уравнений (3.6) чаще всего не прикладывают силы инерции к каждой точке системы с тем, чтобы затем найти их главный вектор и главный момент, а используют готовые выражения для главного вектора и главного момента сил инерций механической системы. Выведем эти выражения.

Из первого уравнения (3.6) следует, что главный вектор сил инерции механической системы равен

а согласно теореме о движении центра масс системы главный вектор внешних сил системы равен

где М – масса системы, ускорение центра масс. Поэтому

(3.7)

т.е. главный вектор сил инерции механической системы равен массе системы, умноженной на ускорение ее центра масс, и направлен в сторону, противоположную этому ускорению.

Из второго уравнения (3.6) находим, что главный момент сил инерции относительно оси z равен

(3.8)

С помощью принципа Даламбера просто и наглядно решаются задачи, в которых по заданному движению системы надо определить реакции наложенных на нее связей. При этом исключается все наперед неизвестные внутренние силы.

3.3 Задание к ргр - м 3

Вертикальный вал АК (рис. 3.2, табл. 3), вращающийся с постоянной угловой скоростью  = 10 с^-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в таблице 3 в столбце 2 (АВ = ВD = DE = ЕК = в). К валу жестко прикреплен невесомый стержень 1 длиной l₁ = 0,4 м с точечной массой т₁ = 6 кг на конце и шарнирно прикреплен однородный стержень 2 длиной l₂ = 0,6 м, имеющий массу т₂ = 10 кг; оба стержня лежат в одной плоскости. Точки крепления стержней к валу указаны в таблице в столбцах 3 и 4, а угол  - в столбце 5.

Пренебрегая весом вала, определить реакции подпятника и подшипника. При окончательных подсчетах принять в = 0,4 м.

Рисунок 3.2

Таблица 3

Номер условия	Подшипник в точке	Стержень 1 в точке	Стержень 2 в точке		Номер условия	Подшипник в точке	Стержень 1 в точке	Стержень 2 в точке	
1	2	3	4	5	1	2	3	4	5
0	В	D	K	30	5	D	К	В	30
1	D	В	Е	45	6	Е	В	К	45
2	Е	D	В	60	7	К	Е	В	60
3	К	D	Е	75	8	D	Е	К	75
4	В	Е	D	90	9	Е	К	D	90