Метод гауса.

Запишемо систему (1) у розгорнутому вигляді:

а11x1+a12x2+...+a1mxm=f1 ,

a21x1+a22x2+...+a2mxm =f2 , (2)

am1x1+am2x2+...+ammxm =fm .

Метод Гаусса розв’язання системи (2) полягає у послідовному вилученні невідомих x1, x2, ..., xm-1 з цієї системи.

Припустимо, що a110 . Поділив перше рівняння на a11, одержимо

x1+c12x2 +...+c1m xm =y1 , (3)

де : c1j=a1j /a11 ; j=2,m ; y1=f1/a11 .

Розглянемо тепер рівняння системи (2), що залишилися

ai1x1+ai2x2+...+aimxm=fi ; i= 2,m . (4)

Помножимо (3) на ai1 та віднімемо одержане рівняння з і-го рівняння системи (4),i=2,m.

У результаті одержимо наступну систему рівнянь:

x1+c12x2+...+c1jxj+...+c1mxm =y1 ,

(1) (1) (1) (1)

a22x2+... +a2jxj+...+a2mxm=f2 ,

............................................ (5)

(1) (1) (1) (1)

am2x2+...+amjxj+...+ammxm=fm .

Tут позначено:

(1) (1)

aij=aij-c1jai1; fi=fi -y1ai1; i,j=2,m . (6)

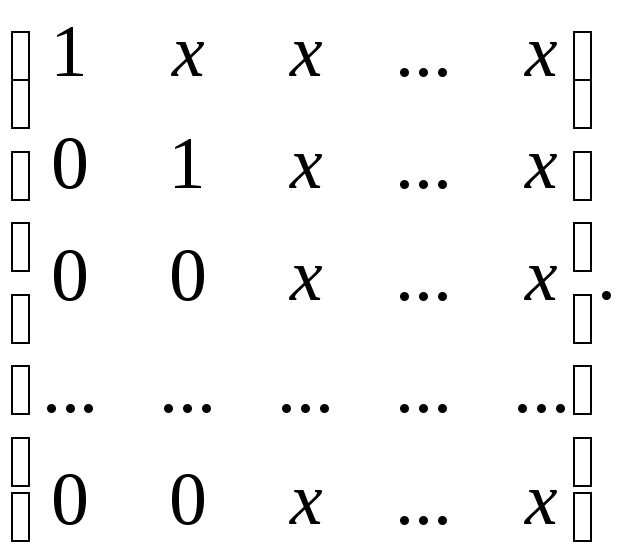
Матриці такої стуктури заведено позначати так:

У системі (5) невідоме х міститься тільки в першому рівнянні, тому у подальшому достатньо мати справу із скороченою системою рівнянь:

(1) (1) (1) (1)

a22x2 +...+a2jxj +...+a2mxm =f2 ,

.............................................. (7)

(1) (1) (1) (1)

am2x2 +...+amjxj +...+ammxm =fm .

Тим самим ми здійснили перший крок методу Гаусса . Коли , то з системи (7) зовсім аналогічно можна вилучити невідоме x2 і прийти до системи, еквівалентній (2),що має матрицю такої структури:

При цьому перше рівняння системи (5) залишається без зміни.

Вилучаємо таким же чином невідомі х 3, х4 ,... ,x m-1 , приходимо остаточнодо системи рівнянь виду:

x1 +c12x2 +...+c1,m-1xm-1+c1mxm =y1,

x2 +...+c2,m-1xm-1+c2mxm =y2 ,

xm-1+cm-1,mxm=ym-1,

xm=ym ,

що еквівалентна початковій системі (2) .

Матриця цієї системи

містить нулі усюди нижче головної діагоналі. Матриці такого виду називаються верхніми трикутними матрицями. Нижньою трикутною матрицею називається така матриця, у якої дорівнюють нулю усі елементи, що містяться вище головної діагоналі.

Побудова системи (8) складає прямий хід методу Гаусса. Зворотний хід полягає у відшуканні невідомих х1, ... ,хm з системи (8). Тому що матриця системи має трикутний вигляд, можна послідовно, починаючи з хm, відшукати всі невідомі. Дійсно, xm=ym,

x m-1 =ym-1 -cm-1,m x m i т. д.

Загальні форми зворотного ходу мають вигляд:

m

xi =yi -  cijxj ; i=m-1,1; xm =ym . (10)

j=i+1

При реалізації на ПК прямого ходу методу Гаусса немає необхідності діяти із змінними x1 ,x2 ,... ,xm. Досить вказати алгоритм, за яким початкова матриця А перетворюється до трикутного вигляду (9),та вказати відповідне перетворення правих частин системи.

Одержимо ці загальні формули.

Нехай вже здійснені перші к-1 кроків, тобто вже вилучені змінні

x1 ,x2,...,xk-1 .

Тоді маємо систему:

x1+c12 x2 +...+c1,k-1xk-1+ c1kxk+....+c1mxm =y1 ,

x2 +...+c2,k-1xk-1+ c2kxk+....+c2mxm =y2 ,

..............................................

xk-1+ck-1,kxk+...+ck-1,mxm=yk-1 , (11)

(k-1) (k-1) (k-1)

akkxk+...+akmxm =fk ,

(k-1) (k-1) (k-1)

amkxk+...+ammxm =fm .

Розглянемо К-те рівняння цієї системи:

(k-1) (k-1) (k-1)

akkxk+...+akmxm=fk,

та припустимо, що . Поділивши обидві частини цього рівняння на, одержимо

xk+ck,k+1xk+1+...+ckmxm=yk, (12)

(k-1) (k-1) (k-1) (k-1)

деckj=akj/akk;j=k+1,m;yk=fk/akk.

Далі помножимо рівняння (12) на та віднімемо одержане співвідношення з i-го рівняння системи (11). У результаті остання група рівнянь системи (11) набуває наступного вигляду:

xk+ck,k+1xk+1 +...+ckmxm=yk,

(k) (k) (k)

ak+1,k+1xk+1+...+ak+1,mxm=fk+1,

.......................................

(k) (k) (k)

am,k+1xk+1+... + ammxm=fm ,

(k) (k-1) (k-1) (k) (k-1) (k-1)

де: aij =aij - aikckj ; i,j=k+1,m ; fi= fi - aikyk ; i=k+1,m .

Таким чином, у прямому ході методу Гауса коефіцієнти рівнянь перетворюються за наступним правилом

(0)

akj =akj ; k,j=1,m ;

(k-1) (k-1)

ckj=akj /akk ; j=k+1,m ; k=1,m ; (13)

(k) (k-1) (k-1)

aij =aij - aikckj ; i,j=k+1,m ; k=1,m . (14)

Обчислення правих частин системи (8) здійснюється за формулами:

(0)(k-1) (k-1)

fk=fk;yk=fk /akk;k=1,m; (15)

(k) (k-1) (k-1)

fi = fi - aikyk ; k=1,m . (16)

Коефіціенти cij і праві частини yi ; i=1,m ; j=i+1,m зберігаються у пам’яті ЕОМ і використовуються при здійсненні зворотнього ходу за формулами (10).

Основним обмеженням методу є припущення, що усі елементи , на які здійснюється ділення, відрізняються від нуля. Числоназиваєтьсяпровідним елементом наК-му кроці вилучення. Навіть, якщо деякий провідний елемент не дорівнює нулеві, а просто є близьким до нуля, в процесі обчислень може мати місце нагромадження похибок. Вихід з цієї ситуації полягає в тому, шо як провідний елемент вибирається не, а інше число ( тобто на К-му кроці вилучається неxk, а інша зміннаxj, ) . Така стратегія вибору провідних елементів здійснюється в методі Гаусса з вибором головного елементу, який буде розглянуто пізніш.

А тепер підрахуємо число арифметичних дій, що необхідні для розв’язання системи за допомогою методу Гаусса. Оскільки виконання операцій множення і ділення на ПК потребує набагато більше часу, ніж виконання додавання і віднімання, обмежимось підрахуванням числа множень і ділень.

1.Обчислення коефіцієнтів за формулами (13) потребує:

(m-k)=1+2+...+(m-1)= ділень.

2.Обчислення усіх коефіцієнтів за формулами (14) потребує

Множень.Тут ми використовуємо за індукцією рівність ),

яку легко перевірити.Таким чином, обчислення ненульових елементівтрикутної матриці С потребує

операцій множення і ділення.

3.Обчисленняправих частинykза формулами (15) потребуєm

ділень,а відшукання за формулами (16)

множень. Разом, обчислення правих частин перетвореної системи (8) потребуєm + m(m-1)/2= m(m+1)дій множення і ділення.

Усього для реалізації прямого ходу методу Гаусса необхідно виконати

дій.

4. Для реалізації зворотнього ходу методу Гауса за формулами (10) необхідно

множень.

Всього, для реалізації методу Гаусса необхідно виконати

дій множення і ділення, причому основний час витрачається на прямий хід. Для великихm число дій множення і ділення у методі Гаусса близьке до За витратами часу та необхідній машинній пам’яті метод Гаусса придатний для розв’язання систем рівнянь (2) загального вигляду з кількістю зміннихmпорядку 100.

УМОВИ ЗАСТОСУВАННЯ МЕТОДУ ГАУСА.

Раніш було показано, що метод Гаусса перетворює вихідну систему рівнянь

(1)

до еквівалентної системи

, (2)

де С- верхня трикутна матриця з одиницями на головнїй діагоналі. З’ясуємо тепер, як зв’язанi між собою вектори правих частинfтаy.

Раніш ми переконалися, що праві частини системи (2) обчислюються за формулами

,

З цих співвідношень можна послідовно одержати

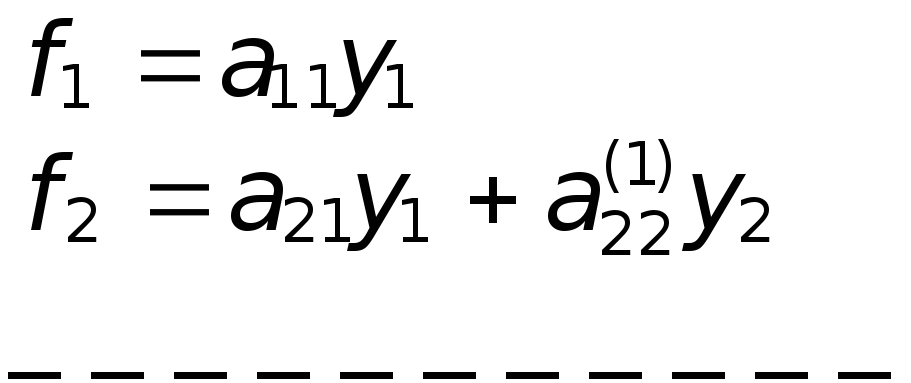
, (3)

де -числові коефіцієнти, причому.

Співвідношення (3) можна записати у матричному вигляді

, (4)

де B-нижня трикутна матриця з елементамина головній діагоналі.

Нагадаємо, що головне припущення при формуліровці методу Гаусса полягало у тому, що усі Тому на діагоналі матриціВстоять ненульові елементи,, тобто В має обернену, a. Підставляючи останнє у (2), приходимо до рівняння

звідки

. (5)

Порівнюючи (5) з рівнянням (1), приходимо до висновку, що як наслідок застосування методу Гаусса одержане розкладання вихідної матриці Ау добутокA=BC, деВ- нижня трикутна матриця з ненульовими елементами на головній діагоналі,С-верхня трикутна матриця з одиничною головною діагоналлю.

Зараз можно тлумачити метод Гаусса таким чином. Нехай задано матрицю A і векторf. Спочатку утворюється розкладАу добуток двох трикутних матриць . Далі послідовно розв’язуються дві системи рівнянь

(6)

(7)

з трикутними матрицями, звідки і одержується шуканий вектор x. РозкладА=ВСвідповідає прямій ході методу Гаусса, а розв’язання системи (6)- (7)- зворотній ході. Зауважимо, що у наведеному раніш алгоритмі розкладA=BC та розв’язання системи (6) провадиться одночасно.

Водночас з сказаного можна зробити наступний висновок. Тому що

,

то метод Гаусса дозволяє одночасно з ров’язаннням системи (1) обчислити визначник матриці Апростим множенням ведучих елементів. Коли ж задачею є просто обчислення визначника матриці, то це можна зробити методом Гаусса, при цьому немає необхідності обчислювати праві частини перетворюємих рівнянь.

Далі, додержуючись стандартних позначень, нижні трикутні матриці будемо позначати L(від англійського lower- нижній), та верхні трикутні - літероюU (від англійського upper-верхній).

Позначимо через -кутовий мінор порядкуj матриці А, тобто

.

Теоретичне обгрунтування можливості розкладу матриці у добуток двох трикутних матриць містить наступна теорема.

Теорема про LU- розклад. Нехай усі кутові мінори матриціАвідмінні від нуля,. Тоді матрицюАможна подати єдиним чином у вигляді добутка

А=LU , (8)

де L- нижня трикутна матриця з ненульовими діагональними елементами іU-верхня трикутна матриця з одиничною головною діагоналлю.

Доведення. Доведемо сформульоване твердження спочатку для матриць другого порядку. Будемо шукати розклад матриці

у вигляді

,

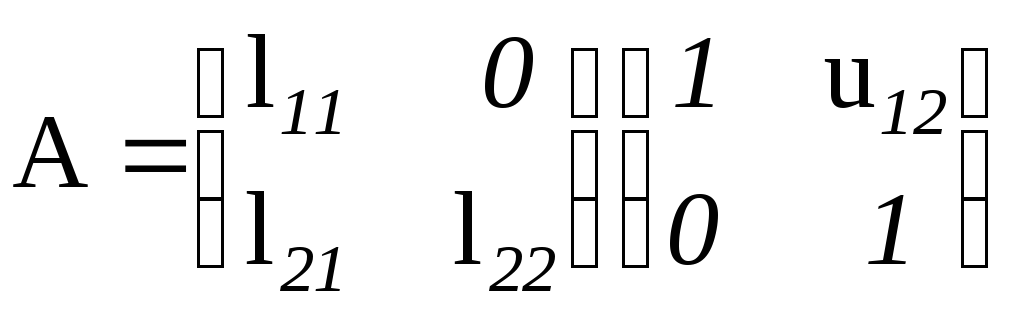де - невідомі досі числа. Для відшукання цих чисел маємо систему рівнянь:

,

яка має єдиний розв’язок

.

За припущенням теореми , тобто елементитавідмінні від нуля.

Подальше доведення проведемо методом математичної індукції. Нехай твердження вірне для матриць порядку доведемо, що воно вірне і для матриць порядкук.

Подамо матрицю АпорядкуКу вигляді

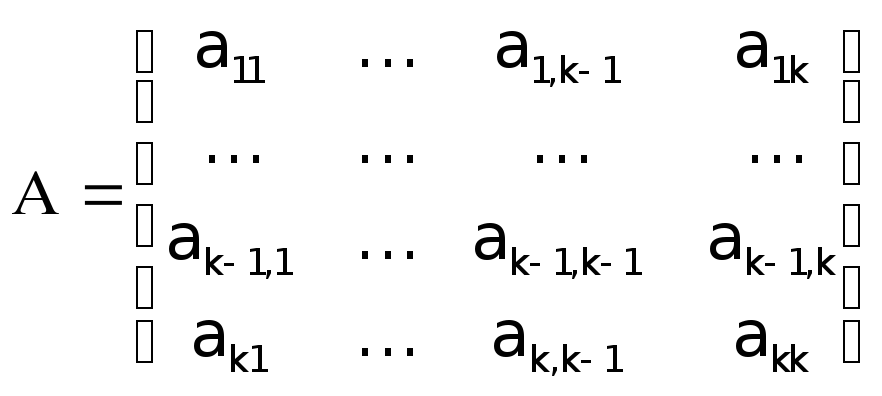
(9)

та позначимо

;,

.

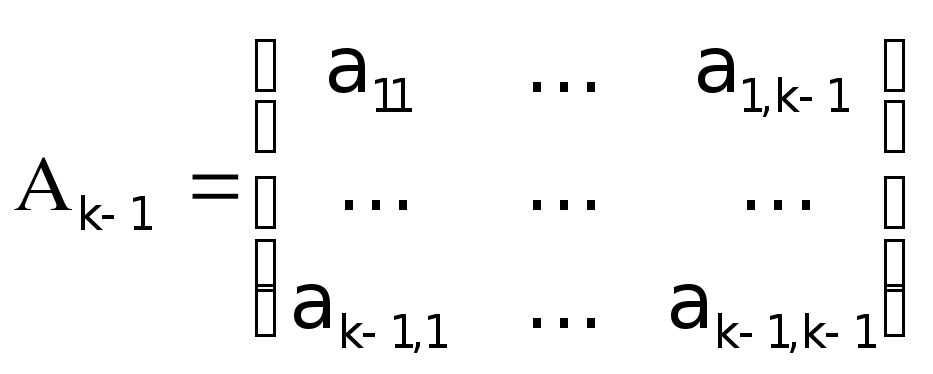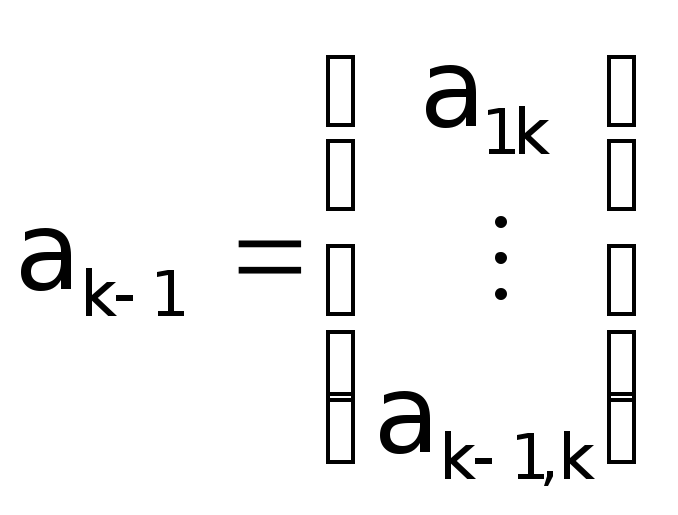Згідно з умовами теореми і тоді за припущеннями індукції існує розклад матриці;

де -відповідно нижня і верхня трикутні матриці, що володіють вказаними у теоремі властивостями. Будемо шукати розклад матриці (9) у вигляді

, (10)

де - невідомі досі вектори.

Помножимо матриці в правій частині рівняння (10) і, враховуючи (9), приходимо до системи рівнянь

; (11)

; (12)

; (13)

З припущенння індукції виходить існування матриць ;. Тому з (11) і (12) одержуємо

;

і,далі, з (13)

.

Таким чином,-розклад матриці А існує. З розкладу (10) виходить, що

.

За умовами теореми , а за припущеннями індукції, і тому. Тим самим індукція завершена і доведена можливість шуканого розкладу.

Доведемо тепер, що такий розклад єдиний. Припустимо, що матрицю Аможна розкласти двома способами

.

Тоді i. (14)

Матриця у лівій частині рівняння (14) є верхньою трикутною, а в правій частині - нижньою трикутною. Така рівність можлива лише у випадку. якщо матриці ідіагональні. Але на діагоналі матриці(а тому і матриці) стоять одиниці, отже ці матриці одиничні

.

Звідси одержуємо ;,тобто розклад (8) єдиний. Теорема повністю доведена.

Зауважимо, що коли хоча б один з углових мінорів матриці Адорівнював нулеві, то вказаний- розклад неможливий. Це легко побачити на прикладі матриць другого порядку.

Висновок. Метод Гаусса можливо використовувати тоді, та й лише тоді, коли усі кутові мінори матриці Авідмінні від нуля.

Було показано, що метод Гаусса приводить до розкладу вихідної матриці у добуток двох трикутних. Більш детально описати структуру цих трикутних матриць можливо за допомогою так званих елементарних трикутних матриць.

Матриця називаєтьсяелементарноюнижньоютрикутноюматрицею, якщо вона має вигляд

.

У матриці усі елементи головної діагоналі окрімдорівнюють одиниці. З решти елементів відмінними від нуля можуть бути лише елементи-го стовпчика, що розташовані нижче. Оберненою доє елементарна нижня трикутна матриця

.

Розглянемо спочатку для наочності систему , що складається з трьох рівнянь:

,

, (15)

.

Після першого кроку виключення за методом Гаусса перетворена система приймає вигляд

,

, (16)

.

Звідси видно, що матриця системи (16) одержується з вихідної матриціАшляхом множенняАзліва на елементарну матрицю

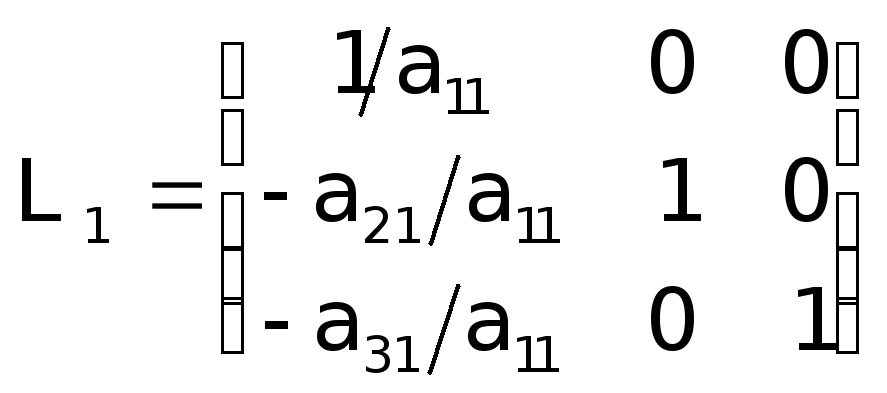(17)

так, що . При цьому систему (16) можна записати у вигляді

.

Матрицю (17) будемо називати елементарною трикутною матрицею, що відповідає першому кроку виключення методу Гаусса.

Перепишемо систему (16) у вигляді

,

, (18)

.

Здійснимо другий крок методу Гауса, тобто виключимо невідому з останнього рівняння.

Тоді одержимо систему вигляду

,

, (19)

.

Можна переконатися,що перехід від (18) до (19) здійснюється завдяки множення системи (18) на елементарну трикутну матрицю

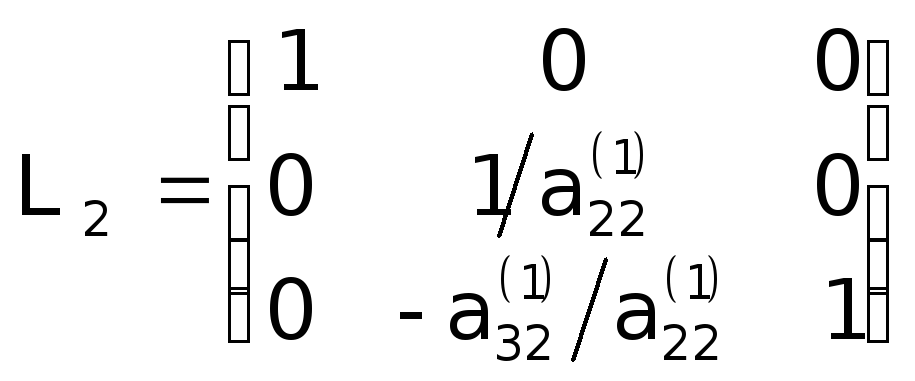. (20)

Таким чином,після другого кроку виключення приходимо до системи

, (21)

де матриці іозначені згідно (17), (20).

Нарешті, перемножаючи (21) на матрицю

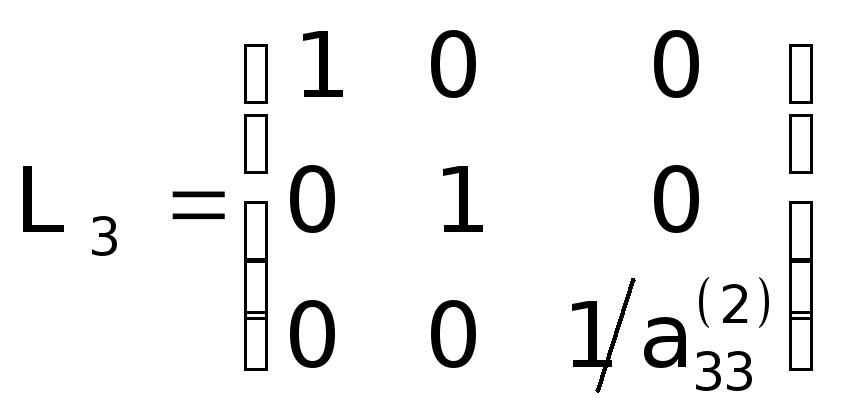
одержимо систему

L₃L₂L₁Ax = L₃L₂L₁f (22)

матриця якої U=L₃L₂L₁A є верхньою трикутною матрицею з одиничною головною діагоналлю.

Звідки виходить, зокрема, що A=LU, деL=L₃^-1L₂^-1L₁^-1 -нижня трикутна матриця.

Таким чином, LU-розклад матриціАможе бути одержаний за допомогою елементарних трикутних матриць: спочатку будуються матриціL_1, L_{2 ,} L₃та обчислюєтьсяU=L₃L, а потім відшукуєтьсяL=L₁^-1L₂^-1L₃^-1.Відзначимо, що матриціL_k^-1мають простий вигляд

; ;;

.

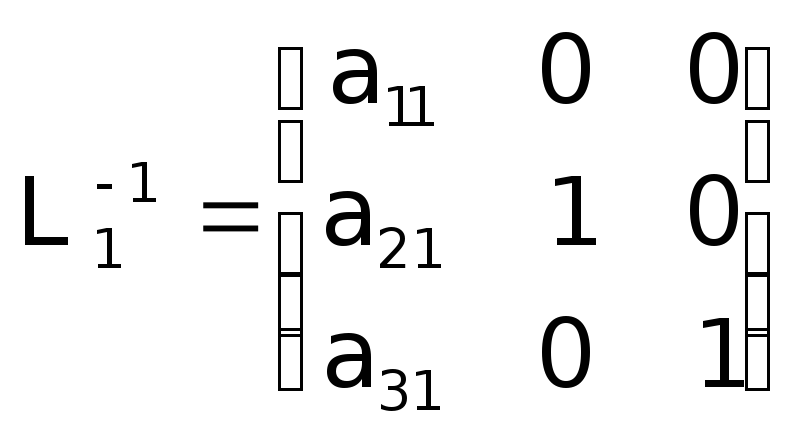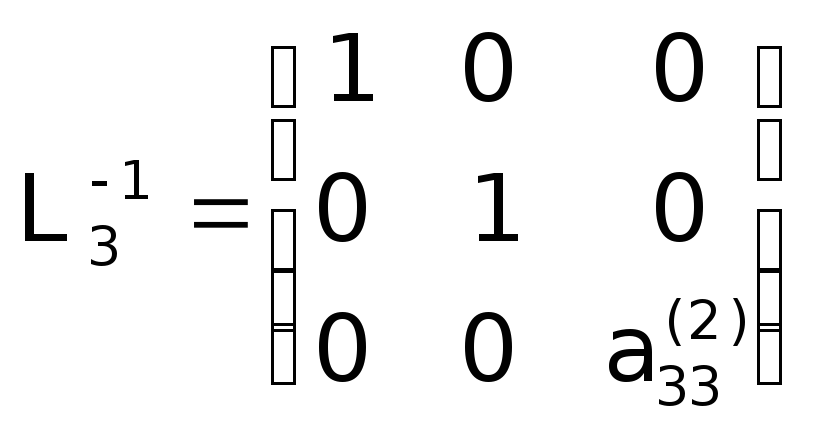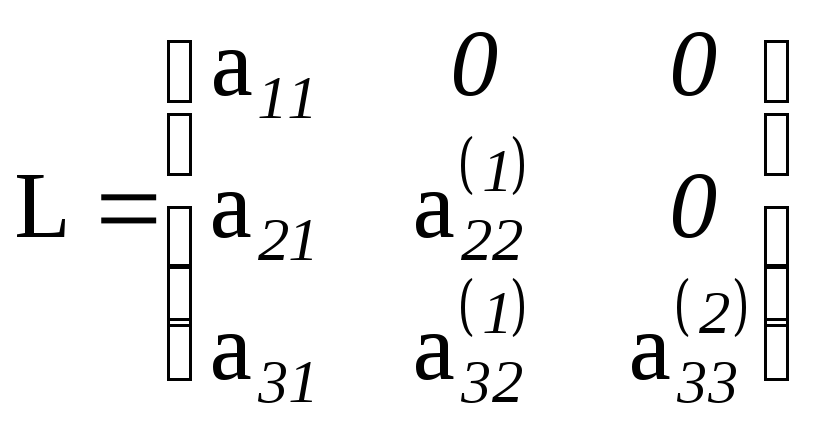причому на діагоналі матриці містяться ведучі елементи методу виключення.

Запис методу Гауса у вигляді (22) детально описує процес виключення.

Усе згадане раніш переноситься на системи рівнянь довільного порядку (2).

Процес виключення можна записати формулою

, (23)

де елементарна нижня трикутна матриця нак-му кроці виключення має вигляд

.

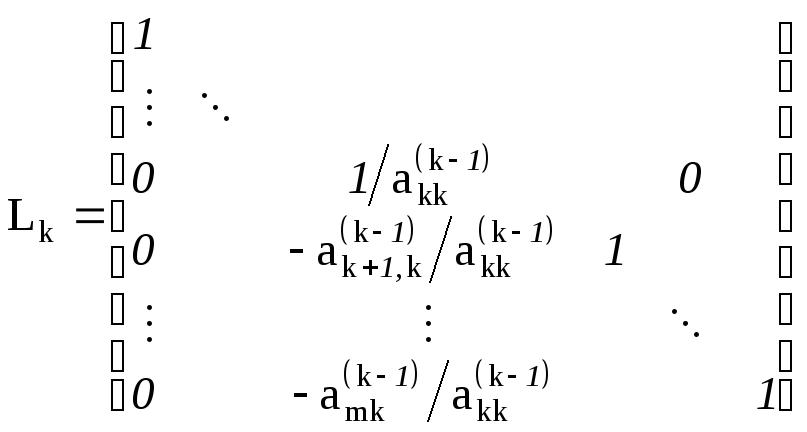Матриця здійснює виключення невідомогоз рівнянь з номерами к+1, к+2, ... ,m.

Матриці існують і мають вигляд

.

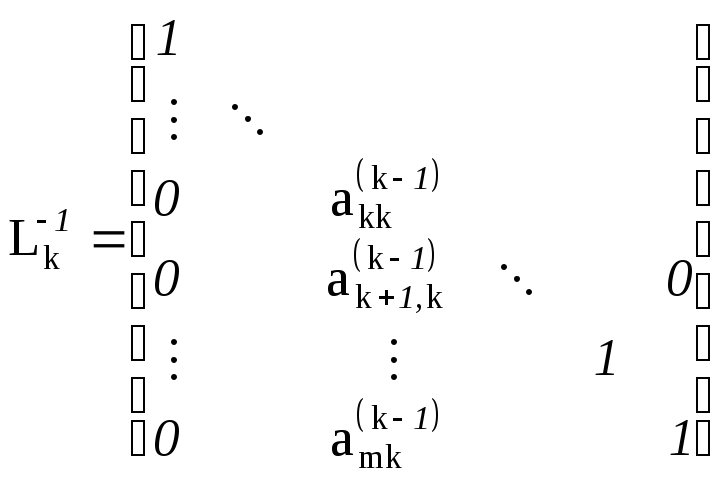Лекція 10 ІТЕРАЦІЙНІ МЕТОДИ РОЗВ’ЯЗАННЯ

СИСТЕМ ЛІНІЙНИХ АЛГЕБРАЇЧНИХ РІВНЯНЬ.

Розглядається система лінійних алгебраїчних рівнянь

(1)

де - квадратна матриця вимірності

- вектор - стовпець правих частин системи;

- вектор - стовпець невідомих.

Ідея найпростіших ітераційних методів розв’язання системи (1) полягає у наступному. За допомогою еквівалентних перетво-рень система (1) зводиться до системи вигляду

(2)

де -квадратна матріця

-відомий вектор.

А потім задається деяке початкове наближення (наприклад, у якостіпершого наближеннябереться вектор, або деякий розв’язок системи (1), який одержується іншим методом з деякою похибкою). Інші наближення послідовно знаходяться за рекурентною формулою

(3)

доки на деякому кроці не буде досягнута задана точність

обчислення значення невідомого вектору .

Виникає питання, за яких умов на послідовність

збігається (у певному розумінні) до точного розв’язку .

Не зупиняючись на подробицях (дивись спецкурс ‘Додат-кові розділи чисельного аналізу’), дамо деякі достатні умови, за яких

або

або

Швидкість збіжності оцінюється нерівністю

де - відстань між векторами та, що може бути заданою:

коли виконується умова (4);

коли виконується умова (5);

коли виконується умова (6).

Задаючи потрібну точність можна з рівності

одержати необхідну кількість ітерацій , щоб досягти задане.

Наведені умови є достатніми для збіжності методу ітерацій, але аж ніяк не необхідними. Необхідні і достатні умови збіжності методу ітерацій дає наступна теорема, яку сформулюємо без доведення.

ТЕОРЕМА: Нехай система (2) має єдиний розв’язок. Послідовні наближення (3) збігаються до розв’язку системи (2) за довільного початкового наближення тоді та й тільки тоді, коли усі власні значення матриціза модулем менше одиниці.

Повернемось зараз до способів приведення (1) до форми (2). Запишемо (1) у розгорнутій формі

Якщо для усіх, то можна (7) зобразити у вигляді

Звідси два найпростіших ітераційних метода.

Метод Якобі, який задається рекурентним співвідношенням:

Метод Зейделя, де вже знайдені компоненти беруться у правій частині співвідношення з (n+1)-го наближення, а інші- зn-го наближення:

Можна дати матричну форму методів Якобі і Зейделя.

Нехай матрицю Анаведено у вигляді:

де -нижня трикутна матриця з нульовою головною діагонал-лю;

D- діагональна матриця зна головній діагоналі;

-верхня трикутна матриця з нульовою головною діагоналлю.

За припущенням існує

Тоді зображенню у формі (8) відповідає

або

Таким чином, методу Якобі відповідає ітераційна процедура

Методу Зейделя відповідає

Використовуючи сформульовані раніш достатні умови збіжності , самостійно переконайтесь, що достатніми умовами збіжності методу Якобі є

або

тобто діагональне переваження матриці А.

Можна довести, що за вказаних умов збігається і метод Зейделя.

Покажемо, що до форми (2), що задовольняє умовам збіжності, може бути зведена довільна система (1) з

Дійсно,візьмемо матрицю де -матриця з достатньо малими за модулем елементами. Множачи (1) зліва наСмаємо

тобто одержали форму (2) з

За рахунок вибору достатньо малих можна задовольнити умовам збіжності.

Процес ітерації, що збігається, володіє властивістю стій-кості, тобто окрема похибка у обчисленнях не позначається на кінцевому результаті, тому що хибне наближення можна роз-глядати як новий початковий вектор.

Лекція 11-13. Диференціальні рівняння

Звичайним диференціальним рівнянням називається рівняння, що містить похідні невизначеної функції і однієї незалежної змінної. Найпростішим звичайним диференціальним рівнянням є рівняння 1-го порядку

y^`=f(x,y). (1)

Основна задача, що відноситься до цього рівняння, є задача Коші: знайти розв’язання рівняння (1)

y=y(x), (2)

яке задовольняє початковій умові y(х₀)= y₀; іншими словами, потрібно знайти інтегральну криву у=(х), що проходить через задану точку М(х_0, y₀) (мал. 1).

у

Якщо права частина f(x,y) непе-

рервна в деякій області R, обумовлений у=у(х)

нерівностями М₀

| x-x₀ |<a; | y-y₀ |<b,

у₀ у то існує щонайменше

одне розв’язання(2), визначене в 0 х₀ х х

межах | x- x₀ |<h, де h- позитивне число.

Рис.1

Це розв’язання єдине, якщо в R виконана умова Липшица

| f( x,y ) – f(x,y) |  N |y – y |, (3)

де N- деяка постійна (сталаЛипшица), що залежить, узагальномувипадку, відaіb. Якщоf(x,y)має граничнупохіднуf_y^` (x,y) уR, то можна покласти

N=max|f ^`(x,y) | при (x,y)R.