3.5 Метод січних

Один з недоліків методу Ньютона — необхідність знаходження похідної f'(х). Якщо знаходження f'(х) ускладнене, то можна скористуватися деяким наближенням, що складають основу методу січних. Замінивши f'(x_n) у методі Ньютона в рівнянні (3.2) різницею послідовних значень функції, віднесених до різності значень аргументу

F^(х_n)=(f(x_n+1)- f(x_n))/( х_n+1 -х_n)

Отримаємо x_n+1 = x_n - f(х_n)/ F^(х_n)

Структура алгоритму має той же вигляд, що і для методу Ньютона (при іншій ітераційній формулі).

Метод січних є комбінацію методів інтерполяції та екстраполяції. В екстраполяційній частині він еквівалентний до методу Ньютона.

Як і в методі Ньютона, розрахунки закінчуються при досягненні необхідної точності послідовних значень х або коли f(х) близько до 0. Тут виникають ті ж труднощі, що і для відшукання кратних коренів.

КОНТРОЛЬНІ ЗАПИТАННЯ

1. Опишіть суть методу хорд.

2. Дати визначення кореня рівняння.

3. Опишіть суть методу половинного ділення.

4. Які методи ефективно застосовувати для гладких функцій?

5. Які методи доцільно використовувати, якщо необхідно знайти всі дійсні корени рівняння?

6. Порівняйте ефективність методу половинного ділення та методу хорд.

7. У яких випадках найбільш ефективно використання методу половинного ділення та методу хорд?

8. Який метод є найбільш надійним при невідомому характері зміни f(x)?

9. Опишіть суть методу Ньютона. У яких випадках найбільш ефективно його використання?

10. У чому полягає різниця між методами Ньютона та січних, і у яких випадках їх використання не ефективно? Наведіть приклади.

11. Які рекомендації в залежності від виду та порядку рівнянь можуть бути використані при виборі методу розв’язання нелінійних рівнянь на ЕОМ?

Лекція 4-5. Початкова обробка даних

При дослідженні в різних галузях науки, техніки чи виробництва ми отримуємо набір даних, які необхідно зберігати та використовувати. Дослідники отримують в найпростішому випадку задану функцію у вигляді таблиці. Наприклад, отримані такі результати 12 вимірів з постійним інтервалом зміни аргументу.

X		Y=F(X)
x1	0	y1	0.142
x 2	5	y 2	0.148
x 3	10	y 3	0.155
x 4	15	y 4	0.152
x 5	20	y 5	0.141
x6	25	y6	0.136
x7	30	y7	0.128
x8	35	y8	0.138
x9	40	y9	0.140
x10	45	y10	0.124
x11	50	y11	0.112
x12	55	y12	0.067

Часто при цьому виникають такі задачі:

1. Знайти значення функції Y для будь-якого значення X

2. Економно відобразити отриманий набір даних.

Перша проблема вирішується методами апроксимації та інтерполяції, а друга – методами апроксимації.

Розглянемо методи апроксимації функції, яка задана таблично.

Апроксимація – це пошук аналітичного виразу (формули ), яка відображає отриманий набір даних. Найчастіше ми шукаємо параметри найпростішої функціональної залежності, тобто лінійної функції:

Y=F(X) = ax + b ( 1 )

Якщо ми отримаємо параметри лінійної функції ( a, b), то можемо знайти значення функції Y для будь-якого значення аргументу. До того ж зберігати потрібно тільки два параметри, а не всю таблицю.

Найпростіший метод пошуку параметрів – це метод двох точок. Суть методу полягає в проведені прямої між двома точками. Як правило, ми використовуємо першу і останню точки. Але в тих випадках, коли ці точки значно відрізняються від основних даних, то можна взяти інші точки.

Для визначення параметрів ( a, b) запишемо значення функції в крайніх точках

y₁ = a x₁ + b

y_n = a x_n + b

Тут n позначає індекс останнього елементу набору даних.

З цих двох рівнянь легко визначити невідомі параметри:

a = ( yn - y1 )/ (xn - x1 )	( 2 )
b = y1 - a x1

Цей метод покажемо на малюнку 1. Червоною лінією ми відображаємо наші табличні дані.

Мал.1

З малюнку видно, що тільки крайні точки збігаються з лінією, а всі останні точки розташовані поза лінією, тобто існує похибка, яку можна записати так:

e_i = y_i - a x_i –b ( 3 )

Недоліком цього методу полягає в тому, що крім двох точок всі останні не використовуються для визначення параметрів апроксимуючої функції.

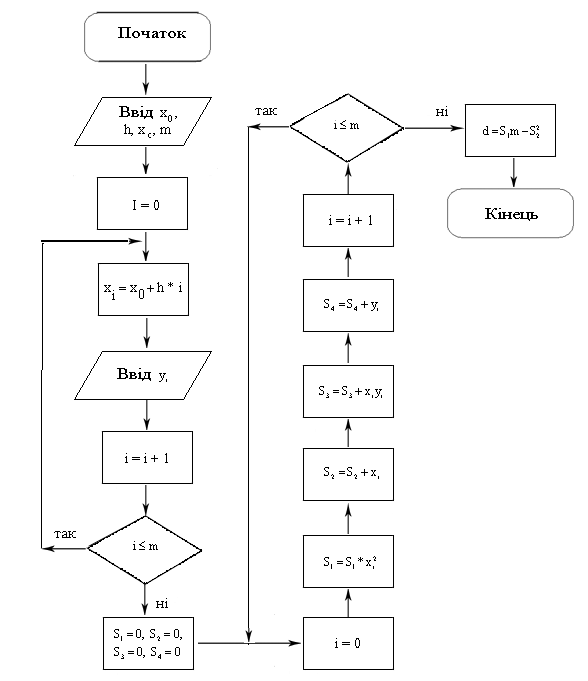
Більш точно відображає набір даних пряма визначена методом нульової похибки.

Суть методу полягає в створенні двох рівнянь з невідомими параметрами апроксимуючої функції. Для цього знайдемо суму похибок першої та другої половини даних і прирівняємо їх 0.

n div 2 n

 e_i = 0  e_i = 0 4 )

i = 1 i = n div 2 +1

Маємо два рівняння і дві невідомі – параметри лінії - ( a, b)

n div 2 n

 (y_i - a x_i –b) = 0  (y_i - a x_i –b) = 0 ( 5 )

i= 1 ndiv2 +1

З цих рівнянь легко визначити параметри прямої лінії.

n div 2 n n div 2 n

a = (  y_i -  y_i ) /( x_i –  x_i ) ( 6 )

i = 1 n div 2 +1 i = 1 n div 2 +1

або

a = (S1 – S2)/(S3-S4) ( 7 )

де

n div 2 S1 =  yi i =1	n div 2 S3 =  xi i =1
n S2 =  yi i = n div 2 +1	n S4 =  xi i = n div 2 +1

Визначивши a легко знайти і параметр b

b = (S1- aS2)/n ( 8 )

Цей метод значно кращий за попередній, бо враховує значення всіх точок. До того ж сума похибок як для першої половини даних, так і для другої дорівнює нулю. Але ці похибки мають різні знаки і можуть сягати великих значень. Щоб уникнути великих відхилень, розглянемо суму квадратів похибок:

G(a,b) =  (e_i)² = (y_i - a x_i –b)² (i= 1…n) (9 )

Звича йно, ми не зможемо отримати

d G(a,b)/da = 0

d G(a,b)/db = 0

d G(a,b)/da = -2 ((y_i - a x_i –b) x_i) =0

d G(a,b)/db = -2 ((y_i - a x_i –b) =0

S1 –bS2 = aS3

S4 –bn =aS2

Графічна інтерпретація апроксимації

Ця функціональна (аналітична) залежність повинна з достатньою точністю відповідати початковій табличній залежності. Критерієм точності для досягнення «хорошого» наближення можуть слугувати декілька умов.

Позначимо через f_i значення, обчислене з функціональної залежності для x = x_i, та співставимо з y_i. Одну з умов узгодження можна записати так:

S = (f_i-y_i)  min ,

тобто, сума відхилень табличних та функціональних значень для однакових x=x_i повинна бути мінімальною (метод середніх). Відхилення можуть мати різні знаки, тому достатня точність в ряді випадків не досягається.

Використання критерію S =|f_i-y_i|  min , також неприпустимо, оскільки абсолютне значення не має похідної в точці мінімуму.

Тому використовують критерій найменших квадратів, тобто визначають таку функціональну залежність, за якої сума квадратів похибок має мінімум:

min S = min (f_i-y_i)² , (1)

В якості функціональної залежності розглянемо поліном:

f(x)=C₀ + C₁X + C₂X²+...+C_MX^M. (2)

Формула (1) має вигляд S = ( C₀ + C₁X_i + C₂X_i²+...+C_MX_i^M - Y_i ) ²

Умови мінімуму S можна записати, прирівнюючи часткові похідні S за незалежними змінними С_0,С₁,...С_М :

S_C0 = 2 ( C₀ + C₁X_i + C₂X_i²+...+C_MX_i^M - Y_i ) = 0 ,

S_C1 = 2 ( C₀ + C₁X_i + C₂X_i²+...+C_MX_i^M - y_i ) X_i = 0 , (3)

S_CM = 2 ( C₀ + C₁X_i + C₂X_i²+...+C_MX_i^M - Y_i ) X_i^M = 0 ,

Тоді з (3) можна отримати систему нормальних рівнянь.

C₀ (N+1) + C₁ X_i + C₂X_i² +...+ C_M X_i^M = Y_i ,

C₀X_i + C₁X_i² + C₂X_i³ +...+ C_MX_i^M+1 = Y_i X_i ,

                                                          (4)

C₀X_i^M + C₁X_i^M+1 + C₂X_i^M+2 +...+ C_MX_i^2M =Y_i X_i^M .

Для визначення коефіцієнтів С_i, та таким чином шуканої залежності (2), необхідно обчислити суми та вирішити систему рівнянь (4). Матриця системи (4) називається матрицею Грама та є симетричною та додатною відносно визначеної. Ці корисні властивості використовуються при її розв’язанні.

	(N+1)	Xi	Xi2	...	XiM	Yi
	Xi	Xi2	Xi3	...	XiM+1	EMBED Equation.3 Yi Xi
	...	...	...	...	...	...
	XiM	XiM+1	XiM+2	...	Xi2M	Yi XiM

Неважко побачити, що для формування розширеної матриці (4а) достатньо обчислити тільки елементи першого рядка та двох останніх стовпців, усі інші елементи не є «оригінальними» та заповнюються за допомогою циклічного присвоєння.

Найпростіша залежність – лінійна,