Перша інтерполяційна формула Гауса:

де m=2i-1,

q=(x-x0)/h.

,

Друга інтерполяційна формула Гауса:

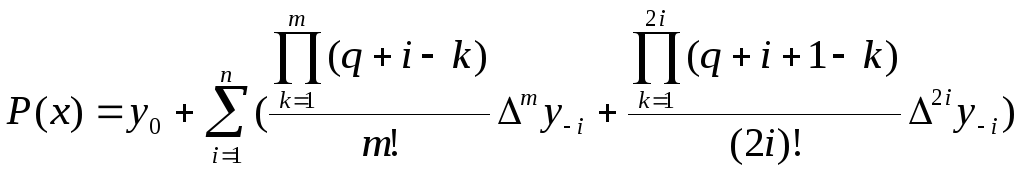
Формули Гауса застосовуються для інтерполяції в середині таблиці поблизу x₀. При цьому перша формула застосовується приx>x₀(тобто вправо), а друга – приx<x₀(вліво).

Інтерполяційна формула Стірлінга

Ця формула являє середнє арифметичне першої та другої формул Ньютона, і одночасно середнє арифметичне першої та другої формул Гаусса:

де m=2i-1,

q=(x-x0)/h.

,

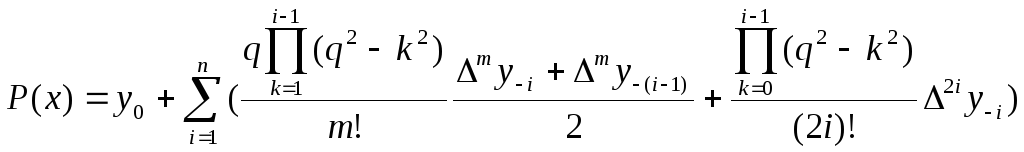Тут варто зауважити, що, коли вузлів непарна кількість, вони нумеровані як x_-n, x_-n+1, ..., x_–2, x_–1, x₀, x₁, x₂, ..., x_-n-1, x_-n, а також що перший доданок під знаком суми містить , що приi=1 дає – пустий множник, у якого верхня межа менша за нижню, тобто він заміняється одиницею.

Формула застосовується для інтерполяції в середині таблиці при значеннях q, близьких до нуля. Практично її використовують при |q| 0.25.

Інтерполяційна формула Бесселя

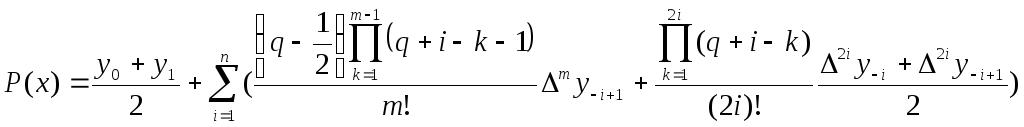, де m=2i-1, q=(x-x₀)/h, нумерація x_-n, x_-n+1, ..., x_–2, x_–1, x₀, x₁, x₂, ..., x_-n-1, x_-n.

Формула Бесселя використовується для інтерполяції в середині таблиці при значеннях q, близьких до 0.5. Практично вона використовується при 0.25q0.75. Найбільш простий вид має формула при q=0.25, тому що всі члени, що містять різниці непарного порядку, зникають. Формулу використовують для ущільнення таблиць, тобто для складання таблиць з дрібнішим кроком.

Інтерполяція для випадку довільних вузлів. Інтерполяційна формула Лагранжа

Нехай x_i – довільні вузли (i=0, 1, 2, ..., n), а y_i=f(x_i) – відповідні значення функції. Багаточленом ступеня n, приймаючим в точках x_i значення y_i, є інтерполяційний поліном Лагранжа:

.

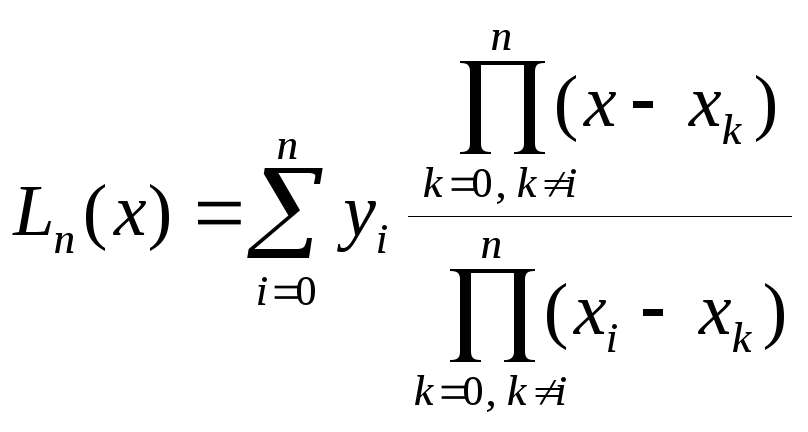Зворотна інтерполяція – це процес знаходження значень x по заданим значенням y. Вона може здійснюватись по будь-якій програмі інтерполяції з довільно розташованими вузлами. При цьому просто замість значень x_і вводять y_і, а замість y_і – значення x_і.

Лекція 8-9. МЕТОДИ РОЗВ’ЯЗАННЯ СИСТЕМ

Лінійних алгебраїчних рівнянь.

Розглянемо чисельні методи розв’язання систем лінійних алгебраїчних рівнянь

Ax=f (1)

де A - матриця m*m, x = ( x1, x2 , ... ,xm ) - шуканий вектор,

f =(f1, f2, ... , fm) -заданий вектор.

Припускаємо, що та визначник матриці А відмінний від нуля, так що існує єдиний розв’язок х. З курсу алгебри відомо,щосистему (1) можна розв’язати за формулами Крамера*. Для великих mцей спосіб практично нереалізований тому, що потребує порядку m!aрифметичних дій. Тому широко використовуються інші методи розв’язання, наприклад,метод Гаусса**, який потребує дій.

Методи чисельного розв’язання системи (1) поділяються на дві групи:

-прямі методи;

-ітераційні методи.

У прямих (або точних) методах розв’язок x системи (1) відшукується за скінченну кількість арифметичних дій.Внаслідок похибок заокруглення прямі методи насправді не приводять до точного розв’язку системи (1) і назвати їх точними можливо лише залишаючи осторонь похибки заокруглення.

Ітераційні методи (їх також називають методами послідовних наближень) полягають у тому, що розв’язок x системи (1) відшукується як границя при послідовних наближеньдеn- номер ітерації. Як правило, за скінченну кількість ітерацій ця границя не досягається.