9. 4.3.1 Пример решения задачи

Какое количество воды вытечет через насадок Вентури внутренним диаметром d = 50 мм за время час при постоянном напоре воды H = 5 м? Какое количество воды вытечет при тех же условиях через коноидальный насадок?

Производительность насадка Вентури

м³/с.

За один час вытечет

м³.

За это же время через коноидальный насадок вытечет

м³.

10. 4.4 Контрольные вопросы

1. Объясните сущность понятий «тонкая стенка» и «малое отверстие».

2. Объясните сущность понятий «сжатое сечение струи», «отверстие с пол-

ным и неполным сжатием», «сжатие совершенное и несовершенное».

3. От каких факторов зависит производительность отверстия?

4. Как определить производительность затопленного отверстия?

5. Что такое коэффициент расхода отверстия?

6. Опишите явление инверсии струи, приведите примеры инверсии при ис-

течении через круглое, квадратное, треугольное отверстия.

7. Что такое насадок? Охарактеризуйте виды насадков, применяемых в технике.

8. Объясните, почему производительность цилиндрического насадка выше

производительности отверстия такого же диаметра.

5. Методики инженерных расчетов

1. 5.1 Классификация трубопроводов и их расчеты

При эксплуатации гидравлических систем возникают два режима (установившийся и неустановившийся) движения рабочих сред: воды, топлива, масел, пара, продуктов сгорания топлива, воздуха и т.д. Неустановившийся режим характеризуется резкой сменой давлений и скоростей в произвольном живом сечении потока с течением времени. Это можно наблюдать в периоды пуска и остановки насосов или компрессоров, регулировки режима с помощью запорно-регулирующей арматуры, в процессе циклической подачи топлива или масла в цилиндры ДВС. Однако большинство систем подавляющее количество времени эксплуатируется в установившемся режиме, поэтому основные приемы расчетов относятся именно к этому случаю.

Гидравлические системы – это совокупность труб различного диаметра, которые различаются характером соединения: последовательное, параллельное, разветвленное. Для удобства расчетов трубопроводы разделяют на простые и сложные, короткие и длинные.

Простые трубопроводы представляют собой последовательное соединение труб не обязательно одинакового диаметра, при условии постоянного расхода жидкости по длине. Сложные – это все остальные виды соединений труб, в том числе и последовательные с переменным расходом жидкости по длине.

Короткие трубопроводы – это такие, у которых местные потери соизмеримы с потерями напора по длине. При расчете длинных трубопроводов местными потерями напора можно пренебречь. Базовой расчетной зависимостью для любой системы является уравнение связи трех определяющих параметров: расхода жидкости Q (м³/с) и напора Н (м), которые обеспечивает насос, и диаметра трубопровода d (м). Поэтому возможны три постановки задачи: рассчитать Н по известным Q и d; определить Q по известным H и d; найти d по известным Q и H.

Для определения необходимого напора суммируют все потери напора

. (109)

При известных значениях расхода (Q) и диаметра трубопровода (d) скорость движения жидкости можно определить как , и тогда расчетная зависимость для короткого трубопровода приобретает вид

. (110)

Расчетная зависимость для длинных трубопроводов имеет более простой вид

. (111)

Полученное значение напора увеличивают обычно на 5…8%. Для другой постановки задачи – определения Q по известным H и d, необходимо уравнение (110) или (111) решить относительно Q

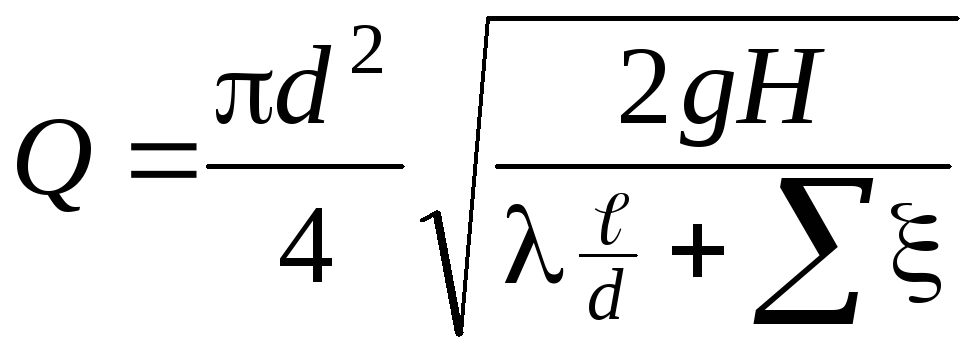. (112)

Однако в связи с тем, что расхода неизвестен, невозможно рассчитать скорость для определения коэффициента гидравлического трения, значением которого необходимо задаться. После определения расхода необходимо проверить корректность полученного результата.

Третья задача – определение диаметра (d) по известным значениям расхода (Q) и напора (Н) - может быть решена только графоаналитическим методом. Для этого следует выбрать несколько значений d и для каждого из них с помощью базовой зависимости (110) или (111) найти значения напоров при заданном значении Q. После этого строится график зависимости d = f(H), с помощью которого по известному значению напора находится необходимая величина d. Однако трубы изготавливаются промышленностью в соответствии с сортаментом и поэтому найденное значение диаметра необходимо увеличить до ближайшего большего по сортаменту.