3й курс 5 семестр / KL_Gidromekhanika_SM

Следовательно, эпюра скоростей представляет сумму отдельных эпюр составляющих движений и имеет вид, показанный на рис. VIII—11. Ее уравнение (при расположении начала координат в середине зазора)

где umax — максимальная скорость напорного течения на оси зазора.

Имея функцию u f (y) , можно легко подсчитать расход через поперечное сечение зазора и силу трения на пластинке.

При перемещении пластинки со скоростью и0, т. е. в противоположном направлении (рис. VIII—12), закон изменения скоростей по сечению зазора будет иметь вид:

7. Полученным решением можно воспользоваться для определения утечек в зазоре между поршнем и цилиндром, если только зазор b мал по сравнению с диаметром D и если поршень расположен в цилиндре соосно.

При неподвижном поршне имеем по формуле (18) после подстановки B D

а при движущемся с постоянной скоростью u0

61

где знак второго слагаемого зависит от направления движения поршня.

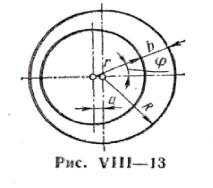
Если поршень расположен в цилиндре с некоторым эксцентриситетом (рис. VIII —13), то зазор b между ними будет величиной переменной в зависимости от угла , причем при малом зазоре

b R a cos r b0 (1 cos ) ,

где Q0 db03 p /12 l — расход в зазоре при соосном расположении поршня в цилиндре.

Из полученной формулы для Q следует, что при максимальном эксцентриситете, т. е. при 1,

Q 2.5Q0

Заметим, что при турбулентном режиме расход при наибольшем эксцентриситете возрастает приблизительно в 1,2 раза по сравнению с расходом при концентричном кольцевом зазоре.

62

8. Рассмотрим течение в клиновом зазоре, вызванное перемещением горизонтальной плоскости относительно поверхности неподвижного башмака, который расположен по отношению к этой плоскости под небольшим углом (рис. VIII—14).

Такой случай имеет место в подшипниках и подпятниках скольжения, и поэтому рассматриваемая ниже задача разъясняет существо процесса, происходящего в смазочном слое.

Пусть угол клина равен и нижняя плоскость движется вправо с постоянной скоростью и0.

Определим расход жидкости в зазоре и закон распределения давления вдоль клина, предполагая поток плоскопараллельным.

Связывая оси координат с неподвижным башмаком и располагая начало координат на уровне нижней движущейся плоскости, выделим в зазоре бесконечно малый элемент жидкости и составим уравнение его движения. Пренебрегая силами инерции по сравнению с силами давления и трения, получаем:

Так как при заданном направлении осей координат (du 0 при dy 0 )

Дважды интегрируя последнее выражение, находим

dp y2 u C1 y C2 dx 2

Для определения постоянных С1 и С2 используем следующие граничные

Расход жидкости в зазоре (на единицу его ширины)

63

Из последнего выражения следует, что расход жидкости через поперечное сечение клина представляет сумму фрикционного расхода и расхода, обусловленного градиентом давления dp / dx вдоль оси х. При некотором значении координаты х = хм градиентdp / dx 0 , и эпюра скоростей в этом сечении клина будет линейной. Для всех координат х < хм, dp / dx > 0, и суммарный расход жидкости равен разности расходов фрикционного и напорного течения; этому случаю соответ-

ме составляющих расходов; эпюра скоростей в поперечном сечении клина показана на рис. VIII—14 справа.

Полагая далее b (a x)tg (a b) , получим следующий закон распределения давлений по длине башмака:

Кривая распределения давлений показана на рис. VIII —14. Исследуя полученную функцию p f (x) на экстремум, находим, что максимум давления имеет

Зная закон распределения давлений, можно вычислить подъемную силу на башмаке и координату, центра давления.

8. Случай течения между параллельными пластинками можно приближенно распространить и на задачу о радиальном течении в торцовом зазоре, образованном двумя плоскими дисками (рис. VIII—15). Определим расход жидкости в зазоре, если последний равен b, а избыточное давление подводимой жидкости на внутреннем радиусе r0 равно р0.

64

Применяя для кольцевого элемента бесконечно малой радиальной длины выведенное ранее уравнение течения между параллельными пластинками, учитывая осевую симметрию течения и пренебрегая силами инерции по сравнению с

Разобранная задача встречается при расчете торцовых уплотнений машин, а также при расчете дисковых фрикционных насосов.

10. При установившемся ламинарном течении в цилиндрической трубе с некруглым поперечным сечением

задача сводится к решению дифференциального уравнения Пуассона при условии равенства нулю скорости на границе потока (частный случай дифференциального уравнения Навье — Стокса);

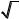
где v — скорость потока, v f (x, y) ; р — перепад давления; х, у — координаты в плоскости поперечного сечения потока; — вязкость жидкости; l — длина трубы.

Решение задачи оказывается сложным, поэтому дадим здесь только окончательные формулы определения расхода для трех поперечных сечений (рнс. VIII— 16):

а) для трубы эллиптического поперечного сечения:

сопротивления трения; DГ — гидравлический диаметр сечения; у — средняя скорость потока; р — потеря давления; — плотность жидкости.

Значения для кольцевых и прямоугольных сечений даны ниже в виде произведения Re :

Кольцевое сечение

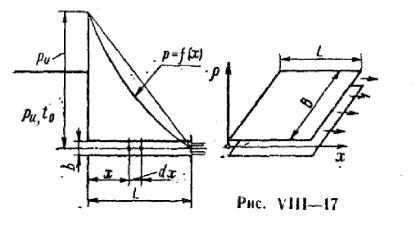
11. Вязкость жидкости изменяется при изменении давления температуры.

Формула (30) позволяет решать задачи ламинарного течения, в которых необходимо учитывать переменность вязкости.

Рассмотрим, например, ламинарное течение жидкости в' зазоре между двумя параллельными пластинками (рис. VIII —17) под действием избыточного давления pИ при начальной температуре t0 . Определим закон изменения давления вдоль зазора, а также расход жидкости через него.

Так как при движении жидкости работа сил трения переходит в тепло, то между давлением и температурой жидкости в каждом сечении зазора существует определенная зависимость.

Пусть в некотором сечении х от входа избыточное давление р и температура t. Тогда, считая, что все тепло, выделяемое в результате внутреннего трения, воспринимается жидкостью и не передается стенкам, можно записать:

через k, получаем:

t tо k( pи p).

Подставляя этот результат в формулу (4.30) и учитывая, что на выходе давление атмосферное (р0 = 0), получаем:

p ( p p)k

или

( k) p kp

оe и

Выделив элементарный участок зазора длиной dх, можем записать по фор-

муле (4.19)

dp 12 Q , dx Bb3

где Q — расход жидкости; В — ширина зазора; b— высота зазора. Разделяя переменные

dp 12Q dx,Bb3

после интегрирования и несложных преобразований получаем следующий закон распределения давления по длине зазора (см. эпюру давлений на рис. VIII— 17):

и расход

Вопросы для самопроверки.

1.Укажите закон распределения касательных напряжений при ламинарном движении.

2.Изобразите закон распределения касательных напряжений и эпюру скоростей в сечении трубопровода при ламинарном движении.

3.Каково соотношение максимальной и средней скоростями при ламинарном течении?

4.Чему равно значение коэффициента Кориолиса при ламинарном движе-

нии?

68

5.От каких параметров зависят потери на трение?

6.В чем состоят особенности движения жидкости на начальном участке ламинарного течения? Как определить длину этого участка и потере в нем?

7.Каковы особенности движения жидкости в плоских и цилиндрических зазорах?

Тема 4.4. Турбулентное течение жидкости в трубах.

Основные понятия турбулентного потока: мгновенная местная скорость, пульсации скоростей и давлений, осредненные скорости и их распределение по сечению. Касательные напряжения в турбулентном потоке. Потери напора. Формула Дарси-Вейсбаха. Коэффициент гидравлического трения. Ламинарный подслой. Шероховатость стенок: абсолютная и относительная. Гидравлически гладкие и шероховатые трубы. Исследования Никурадзе. Формулы для определения коэффициента Дарси и области их применения. Определение потерь напора в трубах некруглого сечения и открытых каналах.

Указания к теме 4.4.

Турбулентное течение характеризуется беспорядочным, хаотичным движением частиц жидкости. Их скорость непрерывно меняется по величине и направлению.

Каждому моменту времени соответствует для каждой частицы своя по величине и направлению мгновенная /местная/ скорость. Изменение во времени этой скорости в данной точке жидкости и есть пульсация скорости. Несмотря на кажущуюся беспорядочность изменения мгновенных скоростей при турбулентном течении, оказывается, что они в данной точке колеблются около некоторой постоянной скорости, называемой осредненной.

Осредненные скорости в данных точках практически постоянны и направлены вдоль потока. Поэтому при турбулентном режиме движения жидкости условно можно рассматривать как параллельно-струйное, что дает возможность применять уравнение Бернулли.

Если для ламинарного течения характерны касательные напряжения вязкостного трения :

л dW , dn

то в турбулентном потоке появляются дополнительные напряжения - турбулентные касательные напряжения

69

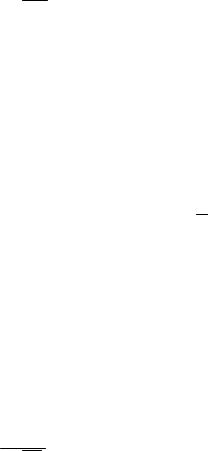
Т dW dn

Здесь η - коэффициент турбулентной вязкости, который в отличие от коэффициента вязкости μ не может быть отнесен к категории физических констант, так как является функцией величин, меняющихся с геометрией и средней скоростью потока жидкости.

Потери напора на трение по длине трубы при турбулентном движении определяются по формуле Дарси, однако коэффициент трения λ определя-

ют по другим зависимостям, чем в ламинарном потоке. В общем случае λ зависит

от числа Рейнольдса Re и относительной шероховатости где d - диаметр d

трубы, а - абсолютная шероховатость стенок.

Характер влияния Rе и ε на сопротивление труб виден на графике Никурадзе, который получен по результатам экспериментов на трубах с искусственной paвномерной шероховатостью.

На графике можно выделить три зоны:

1.Зона гладкого сопротивления /зона гладких труб или Блазиуса/, в кото-

0,3164 4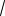Re

2. Переходная зона от гидравлически гладких к шероховатым трубам /зона доквадратичного сопротивления/. В этой зоне λ зависит одновременно от Re и от ε /так как в этой зоне толщина ламинарного подслоя уменьшается, вершины выступов шероховатости создают дополнительную турбулентность и сопротивления в потоке/. Для реальных труб рекомендуется формула Альтшуля:

d

70