3й курс 5 семестр / KL_Gidromekhanika_SM

давления и температуры полная удельная энергия определится суммой кинетической, потенциальной и тепловой удельной энергии.

При движении газов по трубопроводу относительное изменение скоростей незначительно, поэтому с учетом теплообмена между газом и внешней средой можно считать, что по длине потока температура остается постоянной, т. е. процесс изменения состояния газа — изотермический. При расчете газопроводов и воздухопроводов обычно принимают изотермический процесс изменения состояния газа. При изотермическом процессе Т = const и справедливо отношение

p = с,

(3.43)

Постоянное отношение принимают для определенных начальных условий, при которых давление р =р0 и плотность газа при данном давлении и температуре Т0

(3.44)

Применительно к двум сечениям элементарной струйки невязкого газа получим

Уравнения (3.41) и(3.44) является основными при исследованиях и расчетах движения сжигаемого невязкого газа.

51

3.8 УРАВНЕНИЕ БЕРНУЛЛИ ДЛЯ ЭЛЕМЕНТАРНОЙ СТРУЙКИ И ПОТОКА ВЯЗКОЙ ЖИДКОСТИ

Рассеивание энергии, потери напора

Полный напор в любом сечении струйки вязкой жидкости определяется теми же составляющими, что и для невязкой жидкости. Однако значение полного напора в сечениях будет разное, так как часть энергии в вязкой жидкости расходуется на преодоление гидравлических сопротивлений (трение частиц друг о друга, о стенки). При этом часть гидравлической энергии преобразуется в тепловую или механическую (колебание трубопровода) и рассеивается

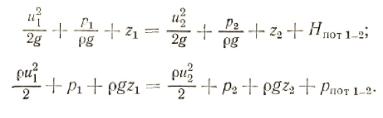(3.48)

Аналогичные коррективы введем и в правые части уравнений для струйки вязкого газа. Тогда

Левые члены уравнений (3.47) - (3.50) дают соответственно полный напор, полное давление, полный запас удельной энергии элементарной струйки в сечении I-I относительно принятой плоскости сравнения.

52

3.10. Поправочный коэффициент к скоростному напору,

определяемому по средней скорости

Основное различие уравнений Бернулли для потока и элементарной струйки заключается в определении скоростного напора в живом сечении. В отличие от элементарной струйки скорости частиц жидкости в различных точках живого сечения неодинаковы, поэтому при определении кинетической энергии через среднюю скорость допускается неточность, которую необходимо учесть.

Кинетическая энергия жидкости в сечении элементарной струйки

u2

где dV — элементарный объем жидкости, проходящий через живое сечение струйки за время t; dV = tdQ = tud . Тогда

Скоростной напор, выраженный через среднюю скорость (3.11), не равен действительному значению, найденному по уравнению (3.52). Отношение действительного скоростного напора к подсчитанному по средней скорости называется коэффициентом Кориолиса:

Для равномерного турбулентного потока = 1 1,13, для равномерного ламинарного потока = 2. На участках неравномерного движения вследствие искажения поля скоростей коэффициент а может иметь различные значения, достигающие 5 и более единиц.

Если в уравнениях (3.47) и (3.48) вместо местной скорости и подставить

2

среднюю скорость , введя поправку к скоростному напору Hск= 2g , по-

лучим уравнение Бернулли для потока

(3.54)

53

Расход жидкости через поперечное сечение зазора шириной:

Очевидно, что средняя скорость такого фрикционного течения равна поло-

вине скорости движения пластинки, т. е. v u0 .

2

При выводе предполагалось, что температура в слое неизменна и, следовательно, вязкость жидкости постоянна.

Приведенные рассуждения позволяют вычислить момент трения на вращающемся с постоянной угловой скоростью валу (рис. VIII—4), концентрически

радиальный зазор; В—диаметр вала.

При малом относительном зазоре кривизной слоя жидкости можно пренебречь, рассматривая движение жидкости в зазоре как плоскопараллельное. Эпюры скоростей и касательных напряжений будут тогда такими, как показано на рис. VIII—5, и момент трения (формула И. П. Петрова)

54

где и0 — окружная скорость вала;

b—длина подшипника. Заметим, что фрикционное движение жидкости в зазоре между валом и подшипником имеет ламинарный характер для чисел Рей-

нольдса, определяемых неравенством Re 30 D , если вращается вал, а подшип-

b

ник неподвижен. В случае же вращения наружного цилиндра

при неподвижном внутреннем ламинарное движение сохраняется в области чисел Рейнольдса Re 2000 , причем число Рейнольдса определяется как

Re u0 Dr u0 2b

vv

3.Если зазор между соосными цилиндрами одного порядка с диаметром одного из них, то предыдущее решение неприменимо. Рассмотрим общее решение такой задачи, определив закон распределения скоростей в зазоре и момент трения на внутреннем цилиндре, если последний расположен соосно с наружным и вращается с постоянной угловой скоростью.

Выделим кольцевой бесконечно малый элемент жидкости, размер которого в радиальном направлении равен dr, а по образующей l (рис. VIII—6).

Поскольку движение жидкости в зазоре является фрикционным, внешними силами, приложенными к выделенному кольцу, являются только касательные силы

трения: 2 rl на его внутренней поверхности и ( d )2 (r dr)l — на наружной. Составляя уравнение моментов сил трения относительно оси вращения, по-

лучаем:

2 rlr ( d )2 (r dr)l(r dr) 0

После несложных преобразований и исключения членов более высокого по-

где А — постоянная.

Рассматриваемое плоское движение является криволинейным, поэтому выражение закона Ньютона (VIII—1) для жидкостного трения здесь неприменимо.

55

Получим выражение закона Ньютона для этого случая движения. Выделим во вращающейся жидкости два слоя на радиусах r и r+dr

(рис.VIII—7) и опреде-

лим скорость сдвига одного слоя относительно другого. За некоторый промежуток

времени t точка А внутреннего слоя переместится в А1 , а точка В, которую примем для простоты рассуждений лежащей на продолжении радиуса точки А, переместится в В2.

Если скорость внутреннего слоя жидкости принять равной и, и скорость наружного слоя u+du, то очевидно дуга АА1 = ut, а дуга ВВ1 =(u+du)t. Следовательно, сдвиг наружного слоя относительно внутреннего

Полученное выражение представляет собой обобщенный закон Ньютона в полярных координатах.

Подставляя в уравнение (6) выражение , получим линейное дифференци-

Отношение приближенного и точного выражений моментов:

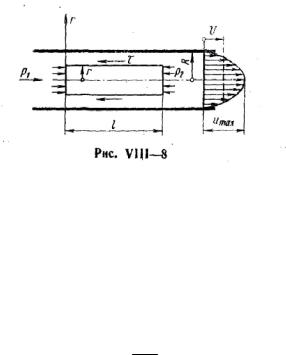
4.Рассмотрим напорное ламинарное движение жидкости в трубе круглого поперечного сечения, вызываемое перепадом давлений по длине трубы.

Выделив объем жидкости в виде горизонтального цилиндра, соосного с трубой (рис. VIII—8), и составив уравнение равновесия приложенных к нему сил,

скорость жидкости на этом радиусе; р — перепад давлений на длине трубы l; p p1 p2 ; r — радиус выделенного цилиндра.

Интегрируя дифференциальное уравнение, получаем закон распределения скоростей по сечению трубы:

Определяя постоянную С из граничного условия, что скорость частиц жидкости на стенке равна нулю находим

где R — радиус трубы.

Скорости распределяются в поперечном сечении трубы по параболическому закону, максимум скорости имеет место на оси трубы:

umax p R2

4 l

Средняя скорость v равна половине максимальной скорости:

57

v umax pR2

2 8 l

Заменяя в этом выражении R через D/2 и р через hП g , где hП — потеря напора и — плотность жидкости получаем:

g D2

v 32 l hП

Решая это уравнение относительно hП , находим выражение потерь напора при ламинарном течении в трубе:

где — коэффициент сопротивления трения ( 64 / Re , здесь Re vD / v ). Расход жидкости через поперечное сечение трубы (формула Пуазейля):

Следует заметить, что полученные выше зависимости, справедливые для стабилизированного ламинарного течения, неприменимы для входного участка трубы, где происходит формирование ламинарного потока. Длина входного начального участка ламинарного течения зависит от диаметра трубы и числа Рейнольдса и определяется выражением:

lнач 0.03Re D .

Для приближенного вычисления потерь на начальном участке можно пользоваться формулой (13), принимая 70 / Re .

5. Более сложным случаем ламинарного движения является осевое течение жидкости под действием перепада давлений в кольцевом зазоре, образованном двумя соосно расположенными цилиндрическими поверхностями (рис. VIII—19).

Чтобы найти закон распределения скоростей по сечению зазора, выделим бесконечно малый кольцевой элемент, рассмотрим действующие на него силы и составим уравнение его движения:

(p1 p2)2 rdr 2 rl ( d )2 (r dr)l 0.

Обозначая р1—р2 = р и пренебрегая членом 2 ld dl , имеющим более высокий порядок малости по сравнению с остальными членами, после несложных преобразований получаем; следующее дифференциальное уравнение: prdr ld ( r) 0 , интегрируя которое (с учетом того, что du / dr ), находим:

58

при r R1 и = 0.

Закон распределения скоростей по поперечному сечению кольцевого зазора будет следующим:

Произведя далее интегрирование скорости по сечению зазора, получим выражение для расхода жидкости:

При R1 =0 выражение (16) переходит в формулу Пуазейля для труб круглого поперечного сечения:

Q R24 p

8 l

6. При решении задачи о плоском ламинарном течении в зазоре между неподвижными параллельными пластинками (рис. VIII—10) из рассмотрения равномерного движения выделенного элемента жидкости приходим к следующему дифференциальному уравнению:

du p y , dy l

где p p1 p2 — перепад давлений на длине зазора l. Интеграл этого уравнения с учетом граничного условия (равенства нулю скорости на стенках) дает

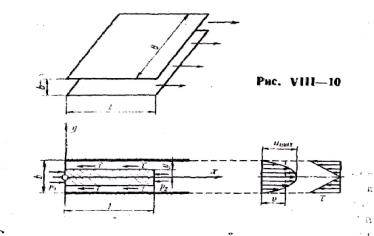
где b — зазор между пластинками.

Закон распределения скоростей по высоте зазора — параболический (в пространстве — параболический цилиндр), средняя скорость

Из последней формулы легко получить выражение для расхода жидкости в зазоре между пластинками

где 96 / Re(Re vDГ / ) ; DГ — гидравлический диаметр ( DГ 2b ).

Если одна из пластинок перемещается параллельно другой с постоянной скоростью и0, то течение жидкости в зазоре будет более сложным, представляя собой сумму двух течений: фрикционного, наведенного перемещением верхней пластинки, и напорного, вызванного перепадом давлений р = р 1 — р2.

60