3й курс 5 семестр / KL_Gidromekhanika_SM

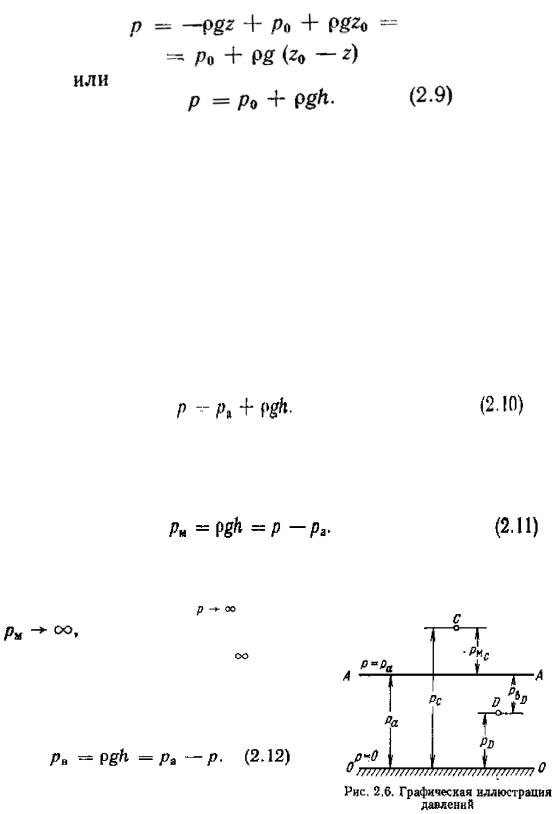
Откуда .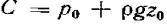

Подставим найденное значение С в полученное после интегрирования выра-

жение

Основное уравнение гидростатики (2.9) выражает зависимость давления в данной точке покоящейся жидкости от рода жидкости и расстояния точки от свободной поверхности. В этом уравнении P — абсолютное давление 1 в данной точке жид-

кости, — абсолютное давление окружающей среды (внешнее давление на свободную поверхность жидкости), g h = p – p0 избыточное давление (давление столба жидкости) в данной точке.

Манометрическое давление и вакуум

В открытых сосудах, водоемах абсолютным давлением окружающей среды является атмосферное давление ра. Для этих случаев уравнение (2.9) будет иметь вид:

Если абсолютное давление в данной точке жидкости больше атмосферного (р > рa), то последний член уравнения (2.10) определяет манометрическое давление

Манометрическое давление представляет собой избыток давления в данной точке над атмосферным. Из уравнения (2.11) можно определить пределы изменения манометрического

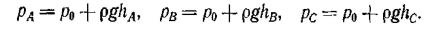
при р → 0 рв→ ра при р = ра рв = 0, т. е. значение вакуума может меняться от 0 до ра.

Проиллюстрируем графически все сказанное выше о вакууме, манометрическом и абсолютном давлениях.

Представим себе плоскость, во всех точках которой абсолютное давление р = 0. След этой плоскости изображен на рис. 2.6 горизонтальной линией 00; А А - след плоскости, абсолютное давление во всех точках которой равно атмосферному р = ра. Таким образом, линия 00 является базой для отсчета абсолютного давления, а линия АА — базой для отсчета манометрического давления и вакуума.

Расстояние от точки С до линии 00 представляет собой абсолютное давление в этой точке pс, а расстояние от точки С до линии АА — манометрическое давление в этой точке рмС.

Аналогично расстояние от точки D до линии 00 представляет собой абсолютное давление в этой точке pDj а расстояние от точки D до линии АА — вакуум в этой точке рBD.

Приведенная на рис. 2.6 схема дает также наглядное представление о пределах изменения манометрического давления и вакуума, которые были установлены выше из выражений (2.11) и (2.12).

Для измерения рассмотренных выше давлений применяют различные измерительные приборы, принцип действия и устройство которых рассмотрены в главе 9.

Закон Паскаля

Поместим на свободную поверхность жидкости, находящейся в равновесии в резервуаре (рис. 2.10, а), поршень и приложим к нему силу 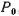, в результате чего со стороны поршня на жидкость возникает давление 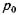. В соответствии с основным уравнением гидростатики (2.9) абсолютные давления в произвольно выбранных точках жидкости А, В, С будут соответственно равны:

Из анализа полученных уравнений видно, что абсолютные давления в точках жидкости, находящихся на разной глубине, будут различные, однако внешнее давление на жидкость, заключенную в замкнутом сосуде, передается всем ее частицам без изменения. В этом суть закона Паскаля.

Практически закон Паскаля используется в ряде гидравлических машин: гидравлических прессах и подъемниках, объемных насосах и гидродвигателях (см. главы 10 и 14) и др.

На рис. 2.10, б приведена принципиальная схема гидравлического пресса. Прикладывая к меньшему поршню силу 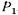, создаем в жидкости давление

22

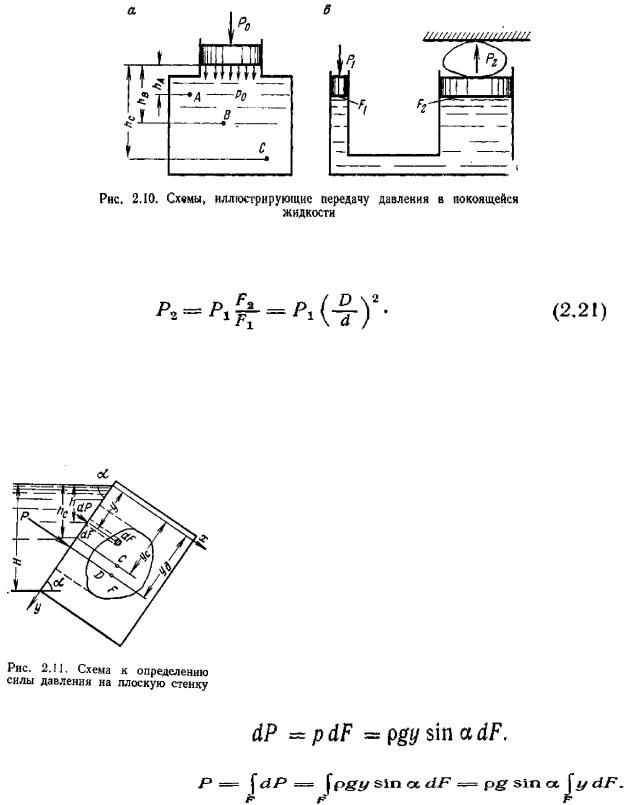
P=P1:F1 которое в соответствии с законом Паскаля передается большему поршню, вызывая силу P2 = pF2. Если пренебречь сопротивлениями, то

Силы давления покоящейся жидкости на плоские стенки

Выделим на плоской боковой стенке сосуда (рис. 2.11), наклоненной в общем случае к горизонту под углом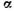, произвольную фигуру площадью F и определим действующую на нее со стороны жидкости силу давления Р.

Для наглядности совместим рассматриваемую стенку с плоскостью чертежа (т. е. повернем ее на 90° вокруг оси у).

Так как давление жидкости в различных по высоте точках площади F разное, то выделим на этой площади элементарную площадку, находящуюся на расстоянии h от свободной поверхности жидкости или y=h/sin от оси х. Для такой бесконечно малой площади давление во всех ее точках одинаково и равно:

P = gh = gsin

следовательно, сила давления жидкости на элементарную площадку будет

Сила давления на всю рассматриваемую площадь F

Выражение y dF представляет собой статический момент рассматривае-

F

мой площади относительно оси х, который равен произведению площади этой

23

фигуры F на расстояние от ее центра тяжести до оси 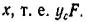Таким образом, 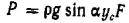или, заменяя 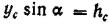,получим

Из уравнения (2.22) видно, что сила давления жидкости на плоскую стенку Р равна произведению смоченной жидкостью площади стенки F на гидростатическое давление в ее

центре тяжести Если на свободную поверхность жидкости действует давление, отличное

от атмосферного, силу давления на стенку можно найти по формулам:

где 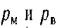- соответственно манометрическое давление и вакуум на свободной поверхности жидкости.

В ряде случаев, кроме значения силы давления жидкости на стенку, необходимо знать координаты Точки ее приложения — центра давления.

Предположим, что сила давления Р приложена в точке D, находящейся от оси х на расстоянии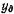. В соответствии с теоремой Вариньона о моменте равнодействующей (момент равнодействующей силы относительно какой-либо оси равен сумме моментов составляющих сил относительно той же оси)

Заменив в последнем выражении Р и 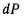их значениями, получим

Вынесем постоянные за знак интеграла и сократим их с аналогичными величинами в левой части уравнения

yc Fy д y 2 dF

F

Выражение y2dF представляет собой момент инерции площади фигу-

F

ры относительно оси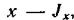 который может быть выражен через момент инерции 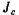относительно центральной оси, параллельной оси х, следующим образом

Из уравнения (2.25) видно, что центр давления для плоской стенки находится

24

всегда ниже ее центра тяжести.

Горизонтальная координата центра давления 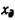находится на оси симметрии площади фигуры.

В частном случае, когда , т. е. для горизонтального дна сосуда, расстояние от свободной поверхности до центра тяжести площади 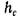будет равно высоте жидкости в сосуде Я, поэтому сила давления жидкости на дно сосуда

Из этого выражения видно, что различные по форме сосуды, имеющие одинаковые площади доньев и заполненные одинаковой жидкостью на одну и ту же высоту, будут иметь одинако-

вую силу давления на дно независимо от формы сосуда и количества находящейся в нем жидкости (гидростатический парадокс). Центр давления, для дна сосуда совпадает с центром тяжести площади.

Силы давления покоящейся жидкости на криволинейные стенки

При криволинейной стенке определение значения, направления и точки приложения силы давления жидкости усложняется, так как элементарные силы давления, действующие нормально на каждую элементарную площадку стенки, имеют разные направления. В этом случае с целью упрощения (чтобы избежать интегрирования по криволинейной поверхности) приходится определять вначале составляющие силы давления по заданным направлениям,

например по осям координат х, у,z, а затем находить результирующую силу давления

Практически приходится иметь дело с криволинейными стенками, представляющими собой поверхности вращения (сферу, цилиндр, конус) и имеющими ось

25

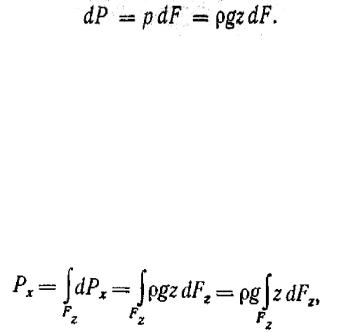
симметрии, лежащую в плоскости, нормальной к стенке, что существенно упрощает определение силы давления жидкости.

Определим силу давления жидкости Р на криволинейную стенку цилиндрической формы, след которой на рис. 2.13— линияMN.

Как и в предыдущем случае, выделим на стенке элементарную площадку dF (след ее на рис. 2.13 -—линия MN), находящуюся на расстоянии z от свободной поверхности. Сила давления Жидкости на эту элементарную площадку

Разложим dP на две взаимно перпендикулярные составляющие: горизонтальную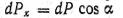 и вертикальную 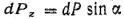и просуммируем отдельно все горизонтальные и все вертикальные составляющее;: Ввиду малости элементарной площадки примем ее за плоскую и спроектируем на горизонтальную ;и вертикальную.; плоскости ..- Проекции. dF будут: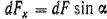;- и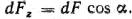

Найдем горизонтальную составляющую силы давления жидкости на криволинейную стенку 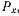, которая представляет собой сумму всех элементарных горизонтальных составляющих Так как, dPx =dPcosα=ρgzdFcosα=ρgzdFz

где 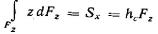— статический момент площади вертикальной проекции криволинейной стенки относительно оси х, проходящей по свободной поверхности жидкости;

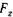— площадь вертикальной проекции смоченной жидкостью криволинейной стенки;

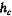— расстояние центра тяжести от свободной поверхности жидкости. Тогда

Таким образом, горизонтальная составляющая силы давления жидкости на криволинейную стенку равна силе давления жидкости на ее вертикальную проекцию [сравните уравнения (2.27) и (2.22)].

Найдем вертикальную составляющую силы давления жидкости на криволинейную стенку 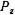, которая представляет собой сумму всех элементарных вертикальных составляющих 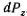. Так как

dPz =dPsin = gzdFsin = gzdFx= gdV

26

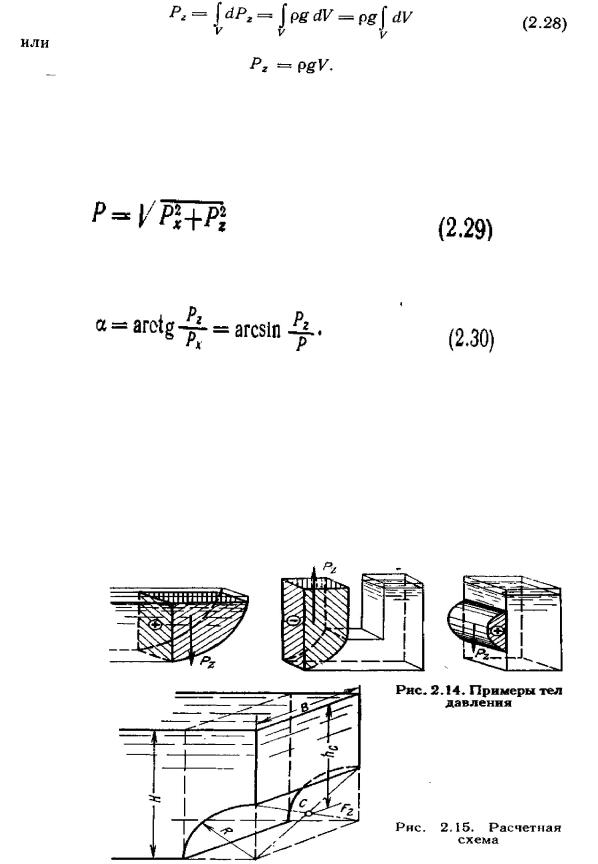
где 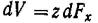элементарный объем жидкости, основанием которого является площадка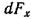, а высотой — расстояние от этой площадки до свободной поверх-

ности жидкости z, то, проинтегрировав 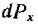по всему объему V, получим

Таким образом, вертикальная составляющая силы давления жидкости на криволинейную стенку равна силе тяжести жидкости в объеме V, называемом телом давления.

Результирующая сила давления жидкости на криволинейную стенку цилиндрической формы Р равна геометрической сумме составляющих

и направлена под углом а к горизонту

Для нахождения тела давления можно воспользоваться следующим определением: тело давления - это объем ограниченный рассматриваемой кривoлинейной стенкой, смоченной жидкостью, вертикальной цилиндрической поверхностью, проведенной через контур этой стенки, и горизонтальной плоскостью, проведенной по свободной поверхности жидкости.

Тело давления условно считается реальным, если его объем, прилегающий к стенке, заполнен жидкостью; составляющая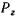 при этом направлена вниз. Тело давления условно считается фиктивным, если его объем, прилегающий к стенке,

27

не заполнен жидкостью; составляющая Рz при этом направлена вверх.

На рис. 2.14 приведено несколько примеров тел давления для криволинейных стенок различной формы.

Пример. Определить силу давления нефти Р на цилиндрическую стенку резервуара (рис. 2.15) и угол наклона линии действия этой силы к ту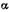,если радиус стенки 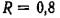м, ширина стенки 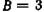м, высота нефти в резервуаре 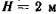. Относительная плотность нефти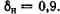

Вертикальная проекция криволинейной стенки представляет собой прямоугольник, площадь которого равна

Расстояние центра тяжести от свободной поверхности нефти равно

Тело давления представляет собой разность объемов параллелепипеда высотой H , шириной В и длиной R и четверти цилиндра с радиусом R и шириной В.

Таким образом, по уравнениям (2.27)—(2.29):

Угол наклона линии действия силы давления к горизонту определим из уравнения (2.30)

Закон Архимеда

Сила, с которой жидкость воздействует на погруженное в нее тело, равна весу жидкости в объеме погруженного тела. Плавучесть тела определяется условиями его равновесия на свободной поверхности.

Плавающее тело при качке может наклоняться в одну и в другую сторону или, как обычно говорят, давать крен. Способность судна выходить из крена в первоначальное положение называется остойчивостью судна.

28

торого V (рис. 2.16). В соответствии с уравнением

(2.26) на поверхность этого тела со стороны жидкости будет действовать сила

Если рассечь тело вертикальными плоскостями, параллельными плоскостям xOz и yOz, таким образом, чтобы площади сечений получились максимальными, то нетрудно показать, что горизонтальные составляющие Рх и Ру равны нулю, так как на каждую из частей будут действовать равные и противоположно направленные силы:

Вертикальная составляющая силы давления жидкости на тело

Где V’- объем ABCDEA, 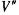— объем AFCDEA,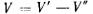результирующий объем тела давления, равный в данном случае объему погруженного в жидкость тела (объему ABCFA) и являющийся фиктивным. '

На погруженное в жидкость тело действует архимедова сила, направленная вертикально вверх и равная силе тяжести жидкости в объеме погруженной части тела. Это и есть закон Архимеда, открытый им в 250 году до н. э.

В уравнении (2.31): Р—архимедова сила, V—объемное водоизмещение (объ-

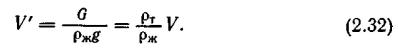
При погружении тела в жидкость может быть три характерных случая:

1., т. е. сила тяжести тела больше архимедовой силы в этом случае их результирующая 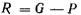будет направлена вниз, следовательно, тело тонет.

2. 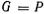, т. е. сила тяжести тела равна архимедовой силе; в этом случае их результирующая , следовательно тело будет находиться в жидкости в состоянии безразличного равновесия (подводное плавание).

3., т. е. сила тяжести тела меньше архимедовой силы в этом случае их результирующая 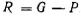будет направлена вверх, следовательно, тело всплывает.

В последнем случае при выходе части тела из жидкости архимедова сила уменьшается и в определенный момент наступит равновесие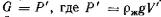 (надводное плавание). Объем погруженной части

плавающего на поверхности жидкости тела может быть найден по формуле

Для равновесия тела при подводном или надводном плавании помимо равенства сил необходимо еще равенство нулю суммарного момента. Последнее условие соблюдается тогда, когда центр тяжести тела лежит на одной плоскости с центром водоизмещения. Более подробно вопросы плавания

тел и устойчивости их равновесия рассматриваются в специальных курсах. Закон Архимеда широко используется при расчете и проектировании су-

дов и других плавающих средств, различных поплавковых устройств (датчиков уровня, дифманометрев поплавкового типа), в гравитационных методах обогащения полезных ископаемых и т. д.

Вопросы для самопроверки

1. Что называют гидростатическим давлением? В каких единицах его выражают? Каковы свойства гидростатического давления?

2. Что называют избыточным, абсолютным давлением, вакуумом? Чему равна наибольшая величина вакуума?

3.Объясните физический смысл величин, входящих в дифференциальные уравнения равновесия жидкости Эйлера?

4.В чем разница между напором и давлением?

5. Что такое поверхность равного давления? Каковы ее формы и уравнения при абсолютном покое, в случае движения сосуда вокруг вертикальной оси?

6.Как формулируется закон Паскаля и какова его связь с основным уравнением гидростатики?

7.Почему центр давления находится ниже центра тяжести смоченной поверхности наклонной плоскости стенки?

30