2.2Вычисление криволинейных интегралов второго рода

Явное представление кривой интегрирования.

Если плоская кривая АВ задана уравнением , , где функция и ее производная непрерывны на отрезке , то криволинейный интеграл вычисляется по формуле .

Параметрическое представление кривой интегрирования.

Пусть кривая АВ задана параметрическими уравнениями x=x(t) и y=y(t), где функции x(t) и y(t) непрерывны вместе с производными на отрезке , причем начальной точке А соответствует значение параметра t=α, конечной точке В значение t=β. Криволинейный интеграл вычисляется по формуле

Пример.

Вычислить криволинейный интеграл .L– контур, ограниченный параболами(рис. 23). Направление обхода контура положительное, т.е против движения часовой стрелки.

Рис. 23

Представим замкнутый контурLкак сумму двух дугL₁ и. На дугеL₁ , хизменяется от 0 до 1, а на дуге ,хизменяется от 1 до 0.

2.3 Формула Остроградского – Грина.

(Остроградский Михаил Васильевич (1861-1862) – русский математик, академик Петербургской А.Н.; Джордж Грин (1793 – 1841) – английский математик)

Иногда эту формулу называют формулой Грина, однако, Дж. Грин предложил в 1828 году только частный случай формулы.

Формула Остроградского – Грина устанавливает связь между криволинейным интегралом и двойным интегралом, т.е. дает выражение интеграла по замкнутому контуру через двойной интеграл по области, ограниченной этим контуром.

Пусть на плоскости Охузадана правильная областьD.

Теорема. Если функции Р(х;у)иQ(х;у) непрерывны вместе со своими частными производнымиив областиD, то имеет место формула

,

где L граница областиD, интегрирование вдоль кривой производится в положительном направлении (при движении вдоль кривойL, областьDостается слева). Формула называется формулой Остроградского-Грина.

Формула Остроградского – Грина справедлива и в случае многосвязной области, т.е. области, внутри которой есть исключенные участки. В этом случае правая часть формулы будет представлять собой сумму интегралов по внешнему контуру области и интегралов по контурам всех исключенных участков, причем каждый из этих контуров интегрируется в таком направлении, чтобы область Dвсе время оставалась по левую сторону линии обхода.

Пример. Решим пример, рассмотренный выше (рис. 23), воспользовавшись формулой Остроградского – Грина.

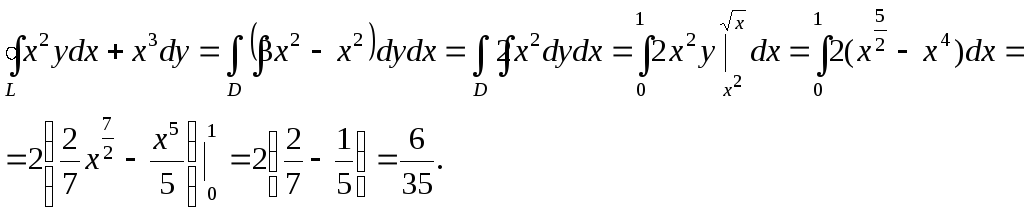
Формула Остроградского – Грина позволяет значительно упростить вычисление криволинейного интеграла.

2.4 Условия независимости криволинейного интеграла II рода от пути интегрирования

Область D называется односвязной, если для любого замкнутого контура, лежащего в этой области, ограниченная им часть плоскости целиком принадлежит D (область «без дыр»).

П

Рис. 24

усть и - две произвольные точки односвязной областиD. ТочкиАиВможно соединить различными линиямиL₁ ,L₂ ,L₃ (рис. 24). По каждой из этих кривых интеграл имеет свое значение. Если же значения по всевозможным кривымАВ одинаковы, то говорят, что интеграл не зависит от вида пути интегрирования. Достаточно для вычисления отметить лишь его начальную и конечную точки пути. Записывают .

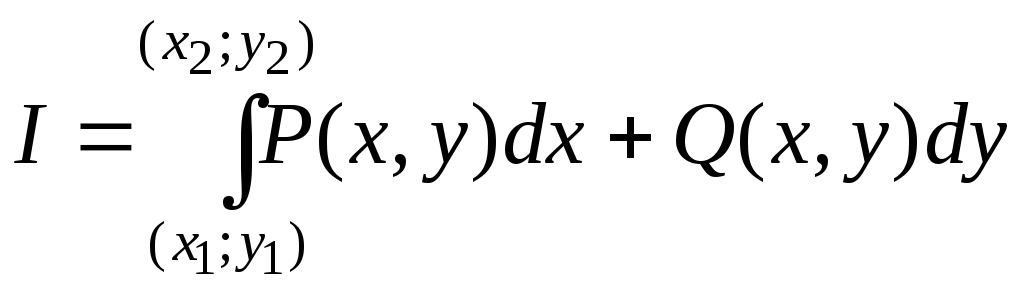Каковы же условия, при которых криволинейный интеграл II рода не зависит от пути интегрирования.

Теорема. Для того, чтобы криволинейный интеграл не зависел от пути интегрирования в односвязной областиD, в которой функциинепрерывны вместе со своими частными производными, необходимо и достаточно, чтобы в каждой точке этой области выполнялось условие .

Следствие. Если выполняется условие , то интеграл по замкнутому контуру равен нулю . Верно и обратное утверждение.