1.2 Вычисление двойного интеграла в декартовых координатах

Требуется вычислить двойной интеграл , где функцияz=f(x,y)≥0 непрерывна в областиD . Как мы выяснили двойной интеграл выражает объём цилиндрического тела, ограниченного сверху поверхностьюz=f(x,y).

Согласно методу параллельных сечений , гдеS(x)-площадь сечения плоскостью, перпендикулярной осиОх ,х=а ,х=b - уравнение плоскостей, ограничивающих данное тело.

Положим сначала, что область D представляет собой криволинейную трапецию, ограниченную прямымих=а ,х=b и кривыми,(рис. 4). Функции и непрерывны и для всех.

Определение. Область Dназываетсяправильнойв направлении осиOy, если любая прямая параллельная осиOy , пересекает границу области не более, чем в двух точках.

Точка - точка входа,

- точка выхода.

Рис. 4

Построим сечение цилиндрического тела плоскостью, перпендикулярной оси Ох :х=const,. В сечении получим криволинейную трапециюABCD , ограниченную линиями, гдех=const,z=0 ,,(рис. 5).

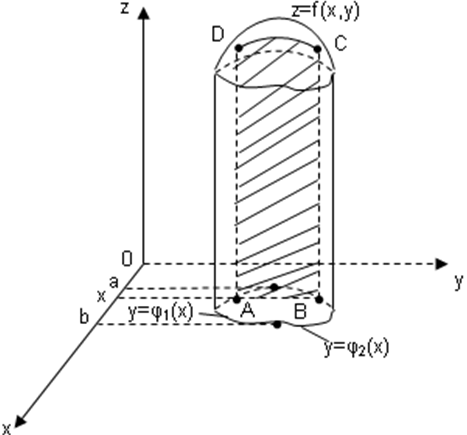Площадь S(x)этой трапеции находим с помощью определённого интеграла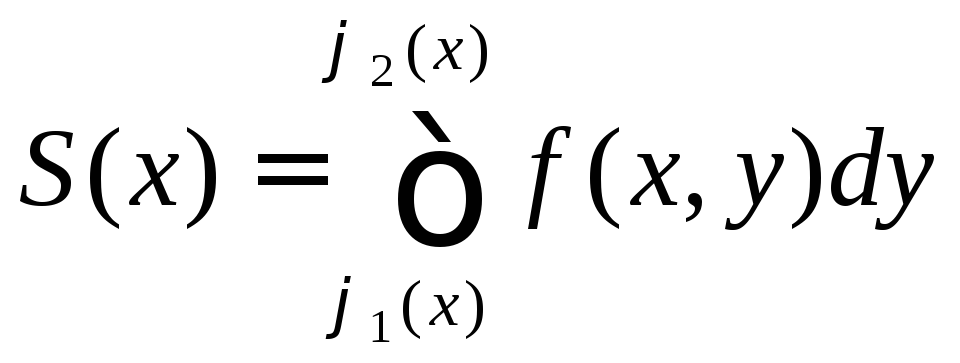

Далее, так как 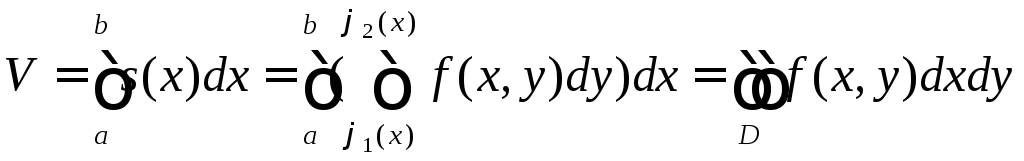это равенство записывают в виде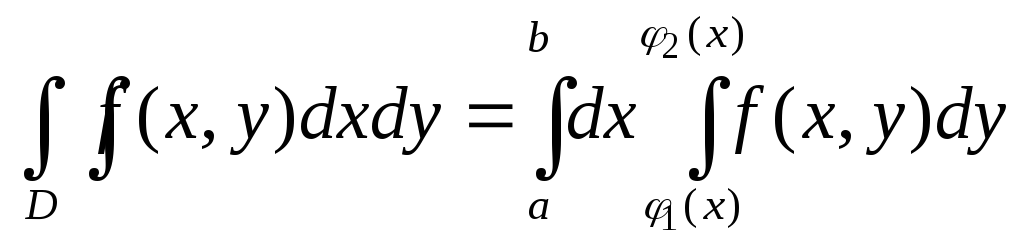(1.2.1)

Рис. 5

Т.о. согласно формуле (1.2.1) вычисления двойного интеграла сводятся к последовательному вычислению двух определённых интегралов.

Правую часть формулы (1.2.1) называют двукратным интегралом от функции f(x,y) по областиD. При этом 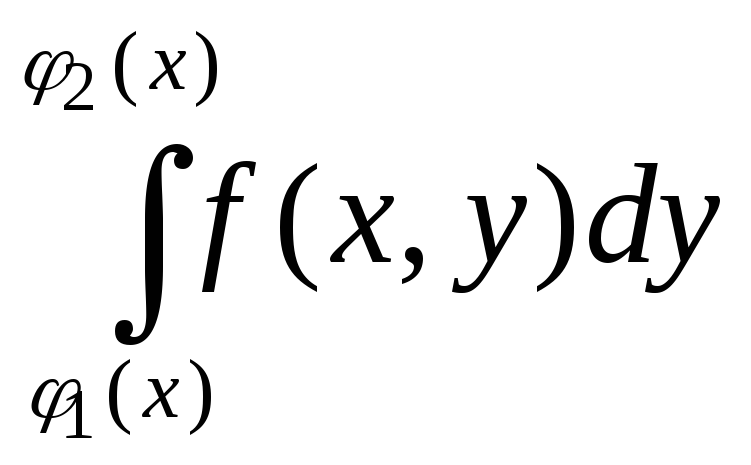называется внутренним интегралом.

Д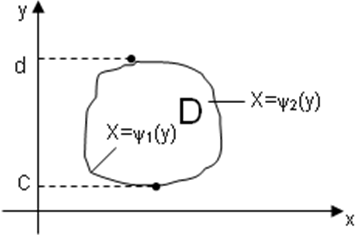ля вычисления двукратного интеграла сначала берём внутренний интеграл, считаяx- постоянным, затем берём внешний интеграл, т.е. результат первого интегрирования интегрируем поxв пределах отадоb .

Если область Dограничена прямымиy=c, y=d (c<d) , кривыми,причёмдля, т.е. областьD- правильная в направлении осиOx(рис. 6). То, рассекая тело плоскостьюy=const , аналогично получим

Рис. 6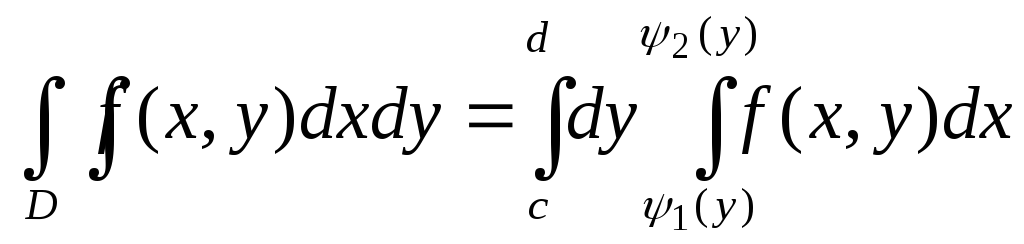

(1.2.2)

Здесь при вычислении внутреннего интеграла считаем y-const

Замечания.

1) Формулы (1.2.1) и (1.2.2) справедливы в случае, когда f(x,y)<0 .

2) Если область Dправильная в обоих направлениях, то двойной интеграл можно вычислять как по формуле 1.2.1, так и по формуле 1.2.2.

3) Если область D не является правильной ни поxни поy , то для сведения двойного интеграла к повторным ее следует разбить на части , правильные в направлении осиOxили осиOy.

4) Полезно помнить, что внешние пределы в двукратном интеграле всегда постоянны , а внутренние, как правило, переменные.

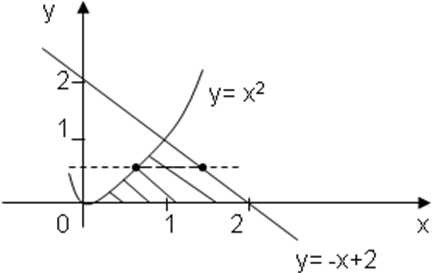Пример:

Вычислить двойной интеграл ,,.

Решение:

Строим область интегрирования (рис. 7). В данном примере удобнее вычислять интеграл по формуле (1.2.2), в направлении оси Ох.

Рис. 7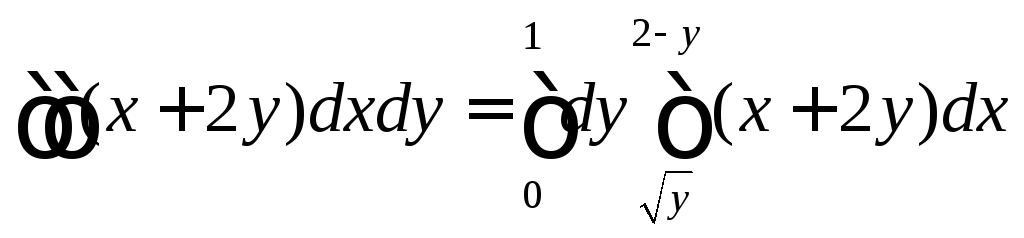

Вычисляем внутренний интеграл, y-const

.

Полученную функцию интегрируем по х

Можно было воспользоваться формулой (1.2.1), но для этого область D следует разбить на две областиD₁иD₂(рис. 8).

Рис. 8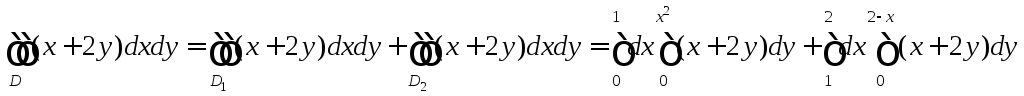

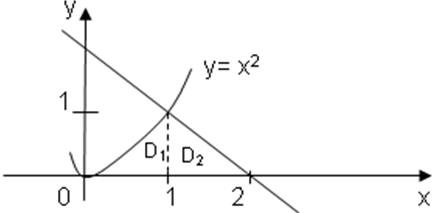
Вычислить самостоятельно двойные интегралы в правой части. Получить тот же результат 29/20.

1.3 Вычисление двойного интеграла в полярных координатах

Для упрощения вычисления двойного интеграла часто применяют метод подстановки, т.е. вводят новые переменные под знаком двойного интеграла.

Введём новые переменные , пусть и, функцииφиψимеют в некоторой областиплоскостиОuvнепрерывные частные производные.

Функциональный определитель

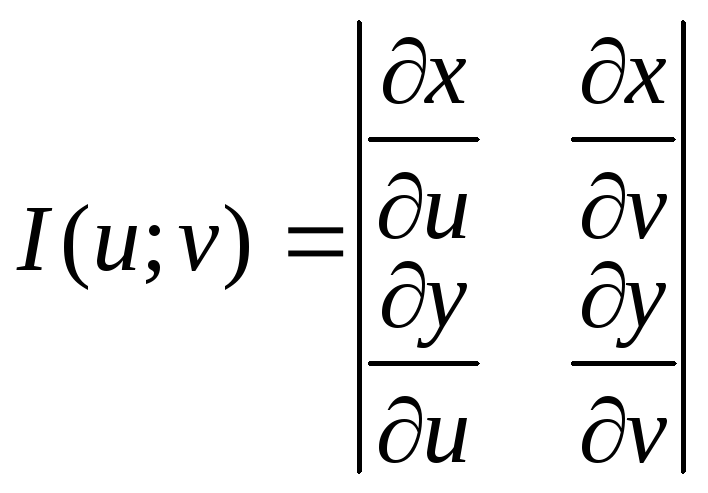- называется определителем Якоби или якобианом.

Если функция непрерывна в областиD , а якобиан, то справедлива формула замены переменных в двойном интеграле

.

Рассмотрим частный случай: замену декартовых координат хиу полярными координатамиr и φ. Прямоугольные и полярные координаты связаны формулами

.

В качестве uиvвозьмём полярные координатыr и φ. Составим Якобиан преобразованияu=r, v=φ.

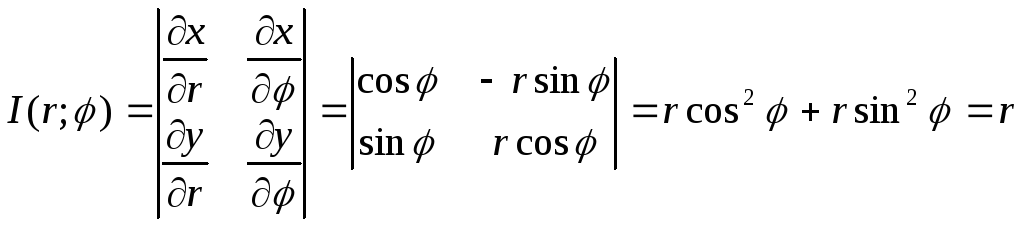
Формула замены переменных x, y в полярных координатах будет иметь вид

- область в полярной системе координат, соответствует области Dв декартовой системе координат.

Д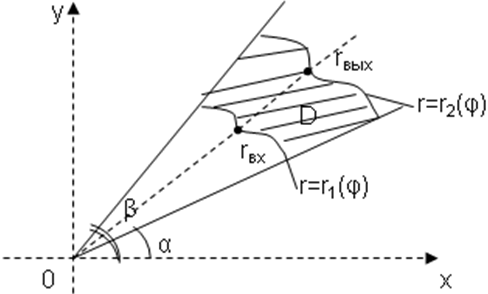ля вычисления двойного интеграла в полярных координатах применяют тоже правило сведения его к двукратному интегралу

Е

Рис. 9

сли область(рис.9) ограниченна лучамиφ=αиφ=β, гдеα<βи кривыми,, где, для любого, т.е. область-правильная: то двойной интеграл в полярной системе координат вычисляется по следующей формуле

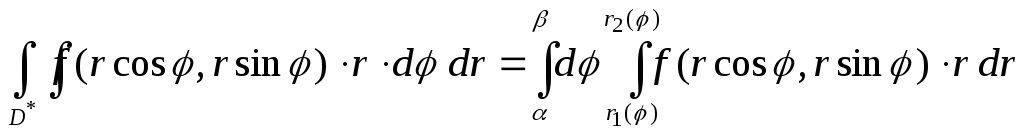
Внутренний интеграл берётся при условии, что φ- константа.

Замечание:

1) переход к полярным координатам полезен, когда подынтегральная функция имеет вид ; областьD - есть круг, кольцо или часть таковых;

2) на практике переход к полярным координатам осуществляется путём замены . Уравнения линий, ограничивающих областьD, так же преобразуются к полярным координатам.

Пределы интегрирования по rи φ находят, совместив декартову и полярную системы координат.

П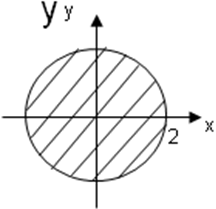ример: Вычислить

D: (рис. 10)

Решение:

Переходим к полярным координатам

Область D в полярной системе координат :

Рис. 10

Подынтегральная функция в полярной системе координат:

Вычисляем интеграл