- •Высшая математика
- •Тема 1. Кратные интегралы.
- •1.2 Вычисление двойного интеграла в декартовых координатах
- •1.3 Вычисление двойного интеграла в полярных координатах
- •1.4 Приложения двойного интеграла
- •1.5 Тройной интеграл
- •1.6 Вычисление тройного интеграла в декартовых координатах
- •1.7 Замена переменных в тройном интеграле.
- •1.8 Геометрические и физические приложения тройных интегралов
- •2. Криволинейные интегралы
- •2.1 Криволинейные интегралы второго рода. Основные понятия
- •2.2Вычисление криволинейных интегралов второго рода
- •2.3 Формула Остроградского – Грина.
- •2.4 Условия независимости криволинейного интеграла II рода от пути интегрирования
- •2.5 Некоторые приложения криволинейного интеграла II рода
- •3. Элементы теории поля
- •3.1 Скалярное поле
- •3.2 Векторное поле
- •3.3 Специальные виды векторных полей
- •3.4 Оператор Гамильтона. Векторные дифференциальные операции
- •4. Числовые и степенные ряды
- •4.1 Числовые ряды. Основные понятия.
- •4.2 Признаки сходимости числовых рядов
- •4.3 Знакочередующиеся ряды и знакопеременные ряды
- •4.4 Степенные ряды
- •4.5 Ряды Тейлора и Маклорена
- •4.6 Разложение некоторых элементарных функций в ряд Маклорена
- •4.7 Некоторые приложения степенных рядов
- •5. Ряды фурье
- •5.1 Периодические функции и процессы
- •5.2 Тригонометрический ряд Фурье
- •5.3 Разложение в ряд Фурье четных и нечетных функций
- •5.4 Разложение в ряд Фурье функций произвольного периода
- •5.5 Представление непериодической функции рядом Фурье
- •6. Элементы операционного исчисления
- •6.1 Оригиналы и их изображение
- •6.2 Свойства преобразований Лапласа
- •6.3 Отыскание оригиналов по изображениям
- •6.4 Операционный метод решения линейных дифференциальных уравнений и их систем
- •98309 Г. Керчь, Орджоникидзе, 82
1.6 Вычисление тройного интеграла в декартовых координатах
 П
П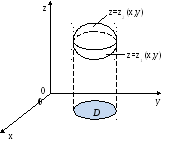 усть
в замкнутой областиV
пространства Oxyz
задана непрерывная функция u=f(x,y,z).
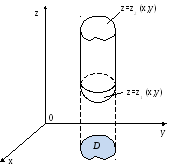
Под областью V
(рис. 13) понимается замкнутая
пространственная область, ограниченная
снизу и сверху поверхностями, определенными
соответственно уравнениями
усть
в замкнутой областиV
пространства Oxyz
задана непрерывная функция u=f(x,y,z).
Под областью V
(рис. 13) понимается замкнутая
пространственная область, ограниченная
снизу и сверху поверхностями, определенными
соответственно уравнениями
![]() и
и
![]() (
(![]() ),
а с боков цилиндрической поверхностью
с образующими параллельными оси Оz.
В частном случае может оказаться, что
образующие цилиндрической поверхности
равны нулю (рис. 14).
),
а с боков цилиндрической поверхностью
с образующими параллельными оси Оz.
В частном случае может оказаться, что
образующие цилиндрической поверхности
равны нулю (рис. 14).
Рис.
13
Переменные x и y изменяются в плоской области D, которая является проекцией на плоскость xOy пространственной области V.
Т
Рис.
14![]()
В декартовых координатах вычисление тройного интеграла сводится к последовательному вычислению трех определенных интегралов.
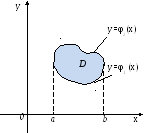
Если плоская
область D
ограничена линиями
![]() и
и
![]() (
(![]() )
и прямыми х=а
и
х=b
(рис. 15),
то тройной
интеграл вычисляется по формуле
)
и прямыми х=а
и
х=b
(рис. 15),
то тройной
интеграл вычисляется по формуле
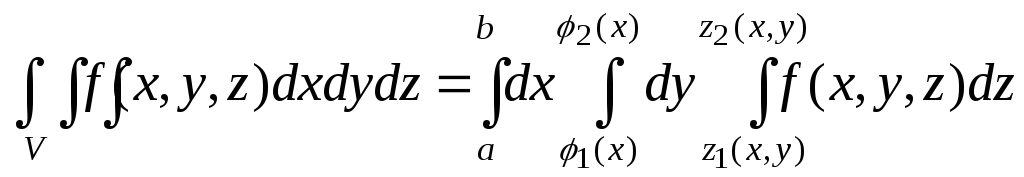 (1.6.1)
(1.6.1)
П
Рис.
15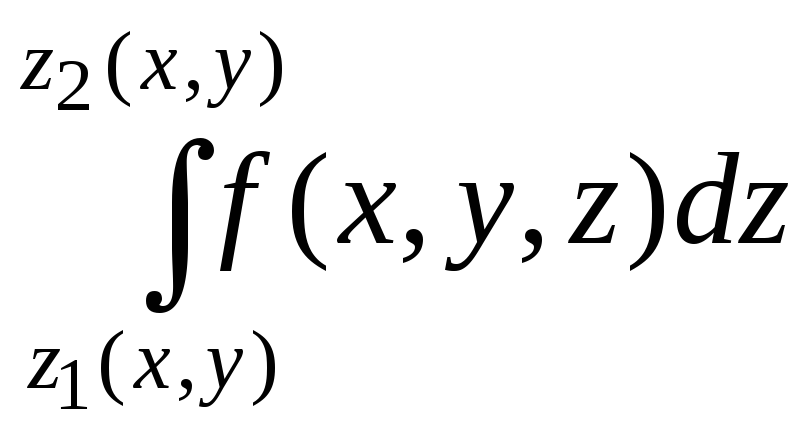 следует рассматривать переменныеx
и y
как постоянные, единственной
переменной величиной при этом является
z.
следует рассматривать переменныеx
и y
как постоянные, единственной
переменной величиной при этом является
z.
Замечание:
1) порядок интегрирования в формуле (1.6.1) может быть изменен;
2) пределы интегрирования во внешнем интеграле всегда величины постоянные.
П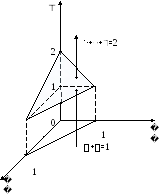 ример.
ример.
Вычислить
интеграл
![]() ,
областьV
ограничена линиями
,
областьV
ограничена линиями
![]() .
.
Решение. Сделаем схематический чертеж (рис. 16) и расставим пределы интегрирования.
![]()
Вычисление начнем с внутреннего интеграла
Рис.
16
1.7 Замена переменных в тройном интеграле.
Операция замены переменных в тройном интеграле аналогична соответствующей операции для двойного интеграла.
Пусть
совершена подстановка
![]() .
Если эти функции имеют в некоторой
областиV*
пространства Ouvw
непрерывные частные производные и
отличный от нуля определитель
.
Если эти функции имеют в некоторой
областиV*
пространства Ouvw
непрерывные частные производные и
отличный от нуля определитель
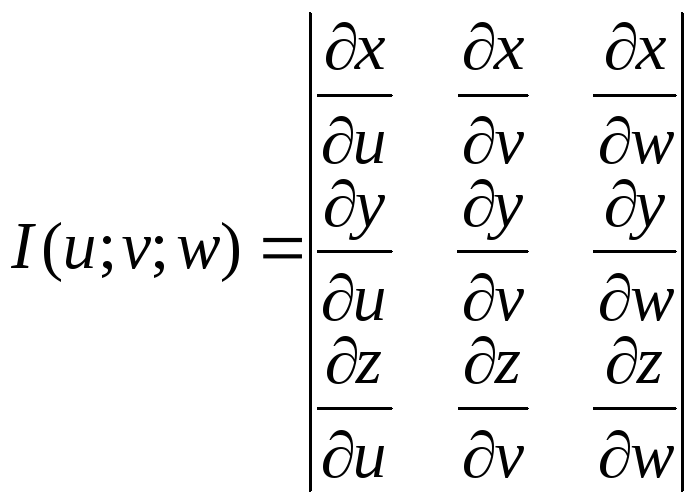 ,
то справедлива
,
то справедлива
формула замены переменных в тройном интеграле:
![]()
Здесь
![]() -
определитель Якоби, или якобиан
преобразования.
-
определитель Якоби, или якобиан
преобразования.
Наиболее часто к замене переменной в тройном интеграле прибегают с целью перейти от декартовой прямоугольной системы координат к цилиндрической или сферической системе.
Рассмотрим эти преобразования подробнее.
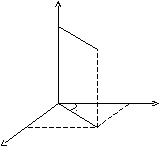
Цилиндрическая система координат.
 z
z
М
z
0
φ x
r
Рис.
17
Положение точки М(x;y;z) в пространстве Оxyz можно определить заданием трех чисел r, φ, z, где r - длина радиус вектора проекции точки М на плоскость Оxy, φ - угол, образованный этим радиус-вектором с осью Оx, - аппликата точки М. Эти три числа (r; φ; z) называются цилиндрическими координатами точки М (рис. 17).
Цилиндрические координаты точки связаны с ее декартовыми координатами следующими соотношениями:
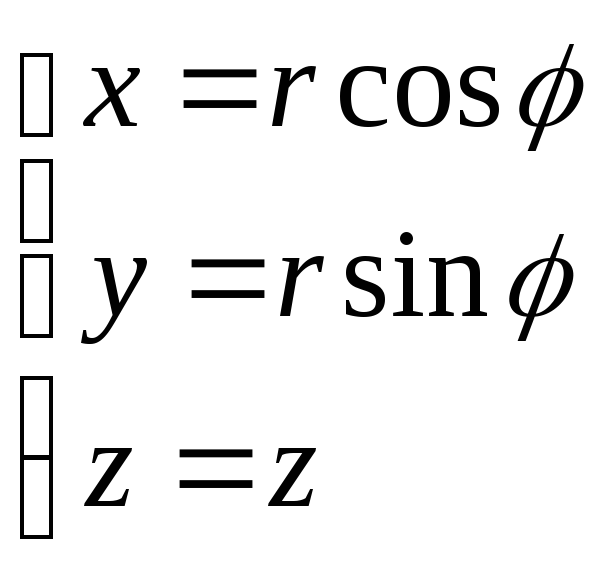
![]()
![]()
Для представления тройного интеграла в цилиндрических координатах вычисляем якобиан:
![]()

Формула перехода тройного интеграла из декартовых координат к цилиндрическим принимает вид
![]() ,
где
,
где
![]()
К
цилиндрическим координатам бывает
удобно прейти, если область интегрирования
образована цилиндрической поверхностью,
проекция цилиндрического тела на
плоскость Oху
является
окружность, а также если подынтегральная
функция имеет вид
![]() .
.
П ример:
Вычислить
ример:
Вычислить
![]() ,
где область V
ограничена верхней частью конуса
,
где область V
ограничена верхней частью конуса
![]() и плоскостью
и плоскостью![]() .
.
Рис.
18
Рис.
19
Решение:
Сделаем схематический чертеж области
(рис. 18). Вычислим интеграл путем перехода
к цилиндрическим координатам:
![]() .
Уравнение конуса примет вид
.
Уравнение конуса примет вид![]() ,
т.е.
,
т.е.![]()
Уравнение окружности
![]() (границы областиD
(рис. 19)) запишется так:
(границы областиD
(рис. 19)) запишется так:
![]() .
Новые переменные изменяются в следующих
пределах:r
– от 0 до 1,
φ – от 0 до 2π, а z
– от r
до 1 (прямая параллельная оси Оz
, пересекающая область D,
входит в конус
.
Новые переменные изменяются в следующих
пределах:r
– от 0 до 1,
φ – от 0 до 2π, а z
– от r
до 1 (прямая параллельная оси Оz
, пересекающая область D,
входит в конус
![]() и выходит из него на высотеz=1).
и выходит из него на высотеz=1).
Таким образом,
получаем
![]()
![]()
![]()
![]()
Сферическая система координат.
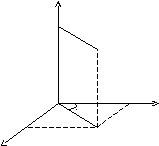
Сферическими
координатами точки М(x;y;z)
в пространстве Оxyz
называется тройка чисел ρ,
φ, θ, где ρ
- длина радиус-вектора проекции точки
М,
φ
- угол, образованный проекцией
радиуса-вектора
![]() на плоскостьОxy
и осью Ох,
θ –
угол отклонения радиуса- вектора
на плоскостьОxy
и осью Ох,
θ –
угол отклонения радиуса- вектора
![]() от осиОz
(рис. 20).
от осиОz
(рис. 20).
 z
z
 М
М
 θ
θ
0 φ x
Рис.
20
y
Связь координат произвольной точки М пространства в сферической системе с координатами в декартовой прямоугольной системе осуществляется по формулам:
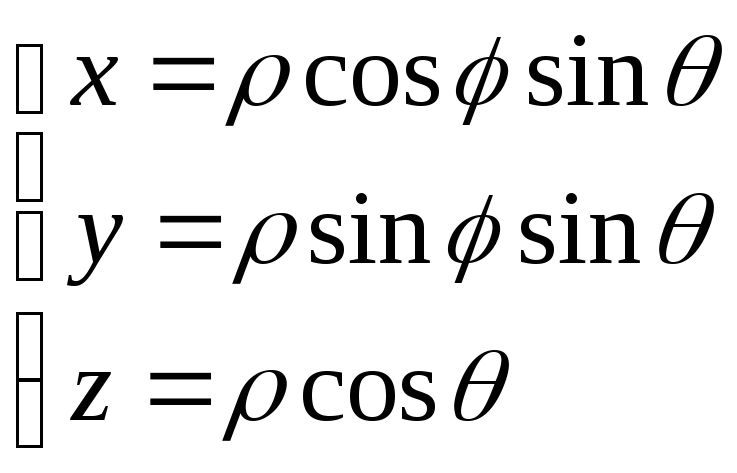 (
(![]() )
)
В некоторых случаях вычисление тройного интеграла удобно производить, перейдя к сферическим координатам.
Для представления тройного интеграла в сферических координатах вычисляем якобиан:
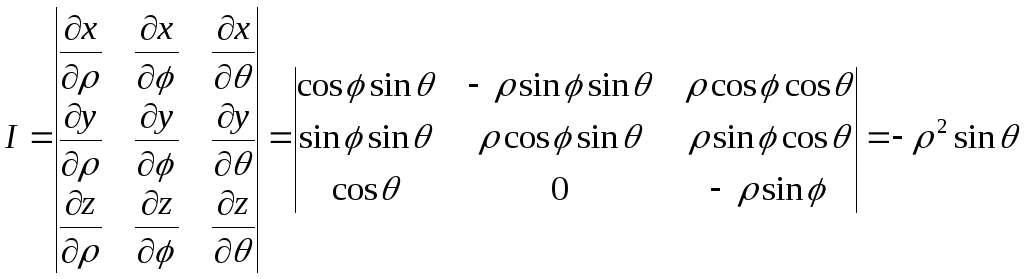
Окончательно получаем:
![]() ,
где
,
где
![]() ,
,
![]() ,
,![]() ,
,![]() .
.
Замечание:
переходить к сферическим координатам
удобно, когда область интегрирования
V
есть шар (уравнение его границы
![]() в
сферических координатах имеет вид
в
сферических координатах имеет вид![]() )
или его часть, а также если подынтегральная
функция имеет вид
)
или его часть, а также если подынтегральная
функция имеет вид![]() .
.
Пример:
найти объем шара
![]() (рис.
21)
(рис.
21)
Решение: найдем 1/8 объема (часть шара, расположенную в первом октанте). Переходим в сферическую систему координат. Уравнение шара в сферической системе координат – ρ=R.
![]()
В ычисляем
три интеграла:
ычисляем
три интеграла:
![]() ,
,
![]() ,
,![]() .
.
![]() .
Окончательно, объем шара
.
Окончательно, объем шара
![]() куб.ед.
куб.ед.